Ebene aus drei Punkten

Gegeben sind drei Punkte und man soll daraus die Gleichung der Ebene bestimmen und die Ebene in einem Koordinatensystem konstruieren. Wichtig hierbei ist, dass die Punkte nicht kollinear sind, also nicht auf einer Geraden liegen.

Gleichung

Es lässt sich aus drei Punkten ziemlich schnell die Parametergleichung aufstellen.

Wir wissen, dass die Parameterform einen Stützvektor und zwei Spannvektoren besitzt, die die Ebene auf diesem Stützvektor aufspannen. Deshalb muss man nur drei Vektoren berechnen: $\overrightarrow{OA}$ , $\overrightarrow{\mathrm{AB}}$ und $\overrightarrow{\mathrm{AC}}$ .

Dann erhalten wir die Gleichung für $E:\;\overrightarrow{\mathrm{x}}=\overrightarrow{\mathrm{OA}}+\mathrm{\lambda}\overrightarrow{\cdot\mathrm{AB}}+\mathrm{\mu}\overrightarrow{\cdot\mathrm{AC}}$

Diese lässt sich dann auch auf die geforderte Darstellungsform umformen.

Im Koordinatensystem

Hier gibt es zwei Möglichkeiten, eine Ebene darzustellen. Entweder nur über die drei gegebenen Punkte oder man ermittelt die Schnittpunkte mit den Achsen und stellt die Ebene damit dar.

1. Möglichkeit

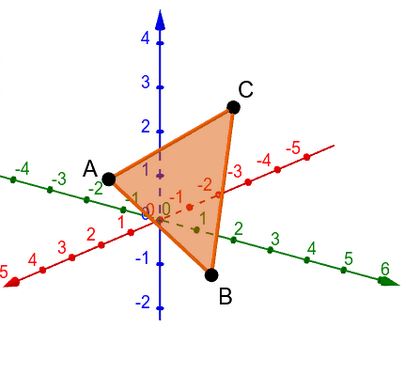
Bei dieser Möglichkeit braucht man nur drei Punkte, die auf der Ebene liegen sollen.

Schritt: Die drei Punkte einzeichnen.
Schritt: Die Punkte mit Strecken verbinden.
Schritt: Das so entstandene Dreieck repräsentiert die gewünschte Ebene.

In dem Applet kann man sehen, wie diese Ebenen-Repräsentation dann aussieht:

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/1775987]

2. Möglichkeit

Hierfür muss die Parameterform erst mal in Koordinatenform umgewandelt werden. Dann berechnet man die Schnittpunkte mit den Achsen und zeichnet diese wie in Möglichkeit 1 ein:

$\;\;\Rightarrow\;\;$ Parameterform in Koordinatenform

$\;\;\Rightarrow\;\;$ Schnittpunkt mit der x-Achse: Setze $y$ und $z$ gleich $0$ .

$\;\;\Rightarrow\;\;$ Schnittpunkt mit der y-Achse: Setze $x$ und $z$ gleich $0$ .

$\;\;\Rightarrow\;\;$ Schnittpunkt mit der z-Achse: Setze $x$ und $y$ gleich $0$ .

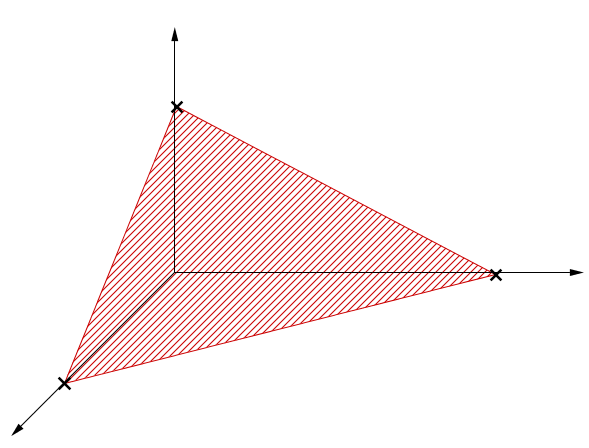
$\;\;\Rightarrow\;\;$ Drei Schnittpunkte einzeichnen (Möglichkeit $1$ )

Beispiel zum Verständnis

Gegeben sind die Punkte $A = (2 / - 2 / 4,5)$ , $B = (- 2 / 3 / 0)$ und $C = (0 / 3 / - 1,5)$

Allgemein	Beispiel
Vektoren $\overrightarrow{OA} , \overrightarrow{\mathrm{AB}}$ und $\overrightarrow{\mathrm{AC}}$ berechnen und in die Parameterform einsetzen.	$E: \overrightarrow{\mathrm x}=\overrightarrow{\mathrm{OA}}+\mathrm\lambda\overrightarrow{\cdot\mathrm{AB}}+\mathrm\mu\overrightarrow{\cdot\mathrm{AC}}$ $\\$ $E: \overrightarrow{\mathrm x}=\begin{pmatrix}2\\-2\\4{,}5\end{pmatrix}+\mathrm\lambda\begin{pmatrix}-4\\5\\-4{,}5\end{pmatrix}+\mathrm\mu\begin{pmatrix}-2\\5\\-6\end{pmatrix}$
Parameterform in Koordinatenform umwandeln	$E:\;7{,}5x+15y+10z-30=0$
Berechnung der Schnittpunkte mit den Achsen: $\\$ Für den Punkt auf der X-Achse setzt man y und z gleich 0. $\\$ Für den Punkt auf der Y-Achse setzt man x und z gleich 0. $\\$ Für den Punkt auf der Z-Achse setzt man x und y gleich 0.	X-Achse: $\\$ $\def\arraystretch{1.25} \begin{array}{l}\mathrm y=\mathrm z=0\;\;\Rightarrow\;\;\;7{,}5\mathrm x=30\\\;\;\Rightarrow\;\;\;\mathrm x=4\\\;\;\Rightarrow\;\;{\mathrm P}_1(4\mid0\mid0)\end{array}$ $\\$ Y-Achse: $\\$ $\def\arraystretch{1.25} \begin{array}{l}x=\mathrm z=0\;\;\Rightarrow\;\;\;15y=30\\\;\;\Rightarrow\;\;\;y=2\\\;\;\Rightarrow\;\;{\mathrm P}_2(0\mid2\mid0)\end{array}\\$ Z-Achse: $\\$ $\def\arraystretch{1.25} \begin{array}{l}x=y=0\;\;\Rightarrow\;\;\;10z=30\\\;\;\Rightarrow\;\;\;z=3\\\;\;\Rightarrow\;\;{\mathrm P}_3(0\mid0\mid3)\end{array}$

Punkte eintragen und nach $1$ . Möglichkeit die Ebene zeichnen.

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Aufstellung von Ebenengleichung

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?