Volumenberechnungen mit Integralen
In der Schule lernst du das Berechnen von Flächen mittels Integralen kennen. Das Gleiche funktioniert aber auch eine Dimension höher. In Abbildung 1 siehst du einen Quader in einem dreidimensionalen Koordinatensystem. Es gilt für die Koordinaten:
.
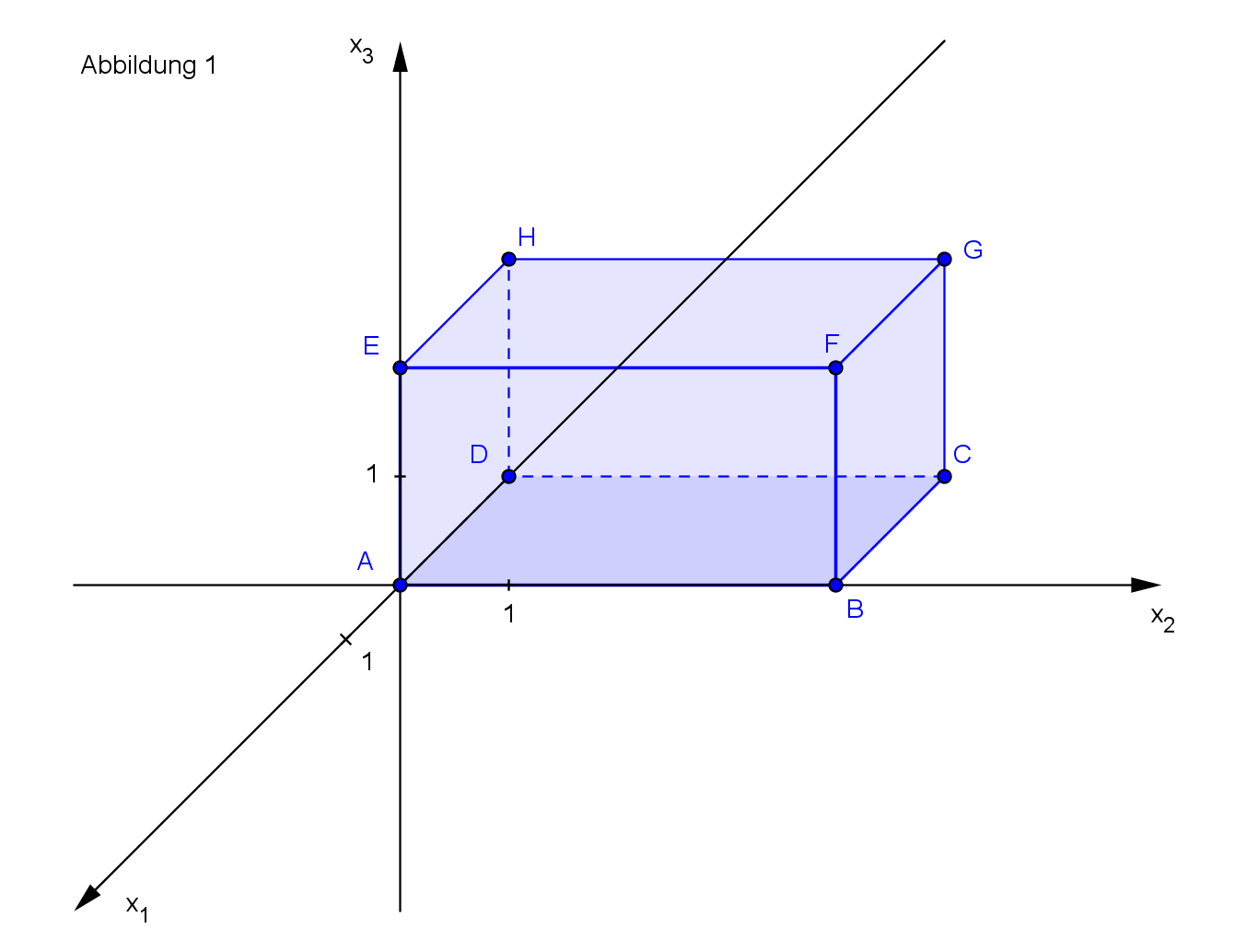
Berechne das Volumen des Quaders mit der Volumenformel.
Betrachte nun in Abbildung 2 die Vorderseite des Quaders. Die Seite ist der Graph der auf definierten Funktion .

Bestimme die Fläche der Quadervorderseite durch integrieren.
Nun wird das Bild "gedreht". In Abbildung 3 siehst du eine seitliche Ansicht des Quaders.

Die Vorstellung bei der Integration ist das schrittweise Ausfüllen der Fläche unter einem Graphen mit Strichen / Balken. Das Gleiche machst du jetzt mit der in die Zeichnung hineingehenden Fläche , um den Quader "auszufüllen".
Bestimme das Volumen des Quaders durch Integration mit dem Integranden .
Ausgehend vom Anfang ist die Volumenformel damit ein doppeltes Integral.
Die Volumenformel für einen Zylinder mit Höhe und Grundflächenradius lautet .
Erkläre, warum diese Formel richtig ist. (Hinweis: Überlege dir, wie der Zylinder nach und nach durch Strecken, Kreise, Flächen o. ä. ausgefüllt wird)
Betrachte jetzt die Volumenformel
Das Volumen welchen Körpers wird mit dieser Formel berechnet?
Zeige, dass die richtigen Ergebnisse liefert, indem du für und berechnest und mit dem Ergebnis der Volumenformel aus der Geometrie vergleichst.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
