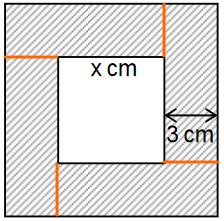
Zwei Quadrate liegen so ineinander, dass jede Seite des inneren Quadrats von der entsprechenden Seite des äußeren Quadrats den Abstand hat. Die Seiten der beiden Quadrate begrenzen eine Fläche mit dem Inhalt , die in der nicht maßstabsgetreuen Abbildung schraffiert dargestellt ist.
Jakob und Lukas sollen die Seitenlänge des inneren Quadrats bestimmen. Sie verwenden dazu unterschiedliche Ansätze:
Ansatz von Jakob:
Ansatz von Lukas:
Erkläre den Ansatz von Jakob in Worten. (1 BE)
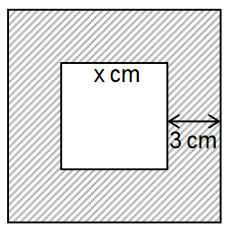
Veranschauliche den Ansatz von Lukas durch geeignete Eintragungen in die obige Abbildung. (1 BE)
Bestimme die Lösung der Gleichung über der Grundmenge . (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?