Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Aufgabe B1

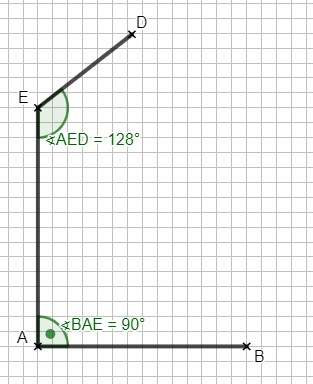
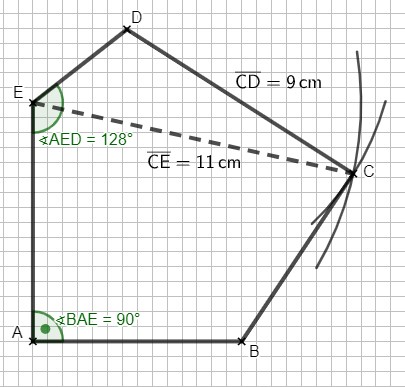
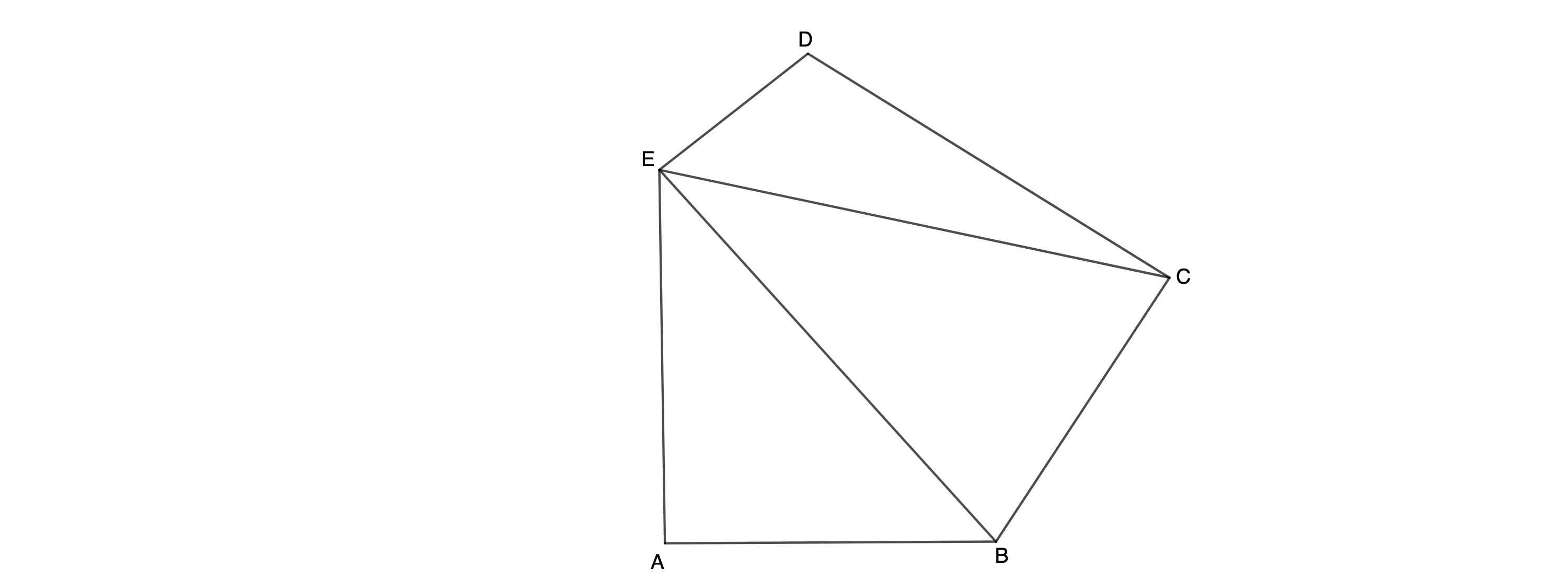
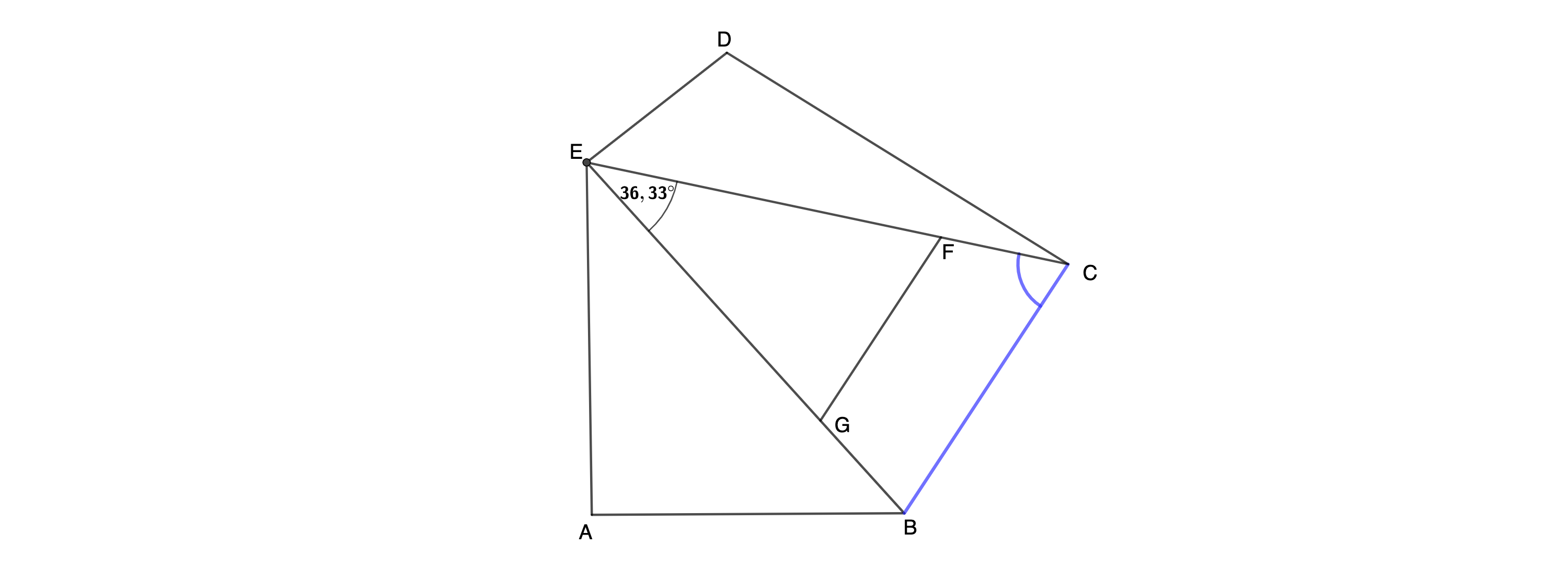
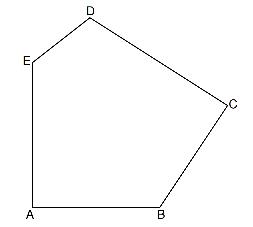
Die Skizze zeigt das Fünfeck $A B C D E$ .

Es gilt: $\overline{AB}= 7\;\text{cm}$ ; $\overline{AE}= 8\;\text{cm}$ ; $\overline{DE}= 4\;\text{cm}$ ; $\overline{CE}=11\;\text{cm}$ ; $\overline{CD}=9\;\text{cm}$ ;

$\sphericalangle{BAE}=90°$ ; $\sphericalangle{AED}=128°$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Zeichnen Sie das Fünfeck $A B C D E$ sowie die Strecken $[B E]$ und $[C E]$ .
Berechnen Sie sodann die Länge der Strecke $[B E]$ und das Maß des Winkels $A E B$ . (4 P)
$[$ Teilergebnisse: $\overline{BE}=10{,}63\;\text{cm}$ ; $\sphericalangle{AEB}=41{,}19°$ $]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pythagoras
Zeichnen des Fünfecks
Zeichne zuerst mit dem Geodreieck die Strecke $\left[AB\right]$ , den Winkel $\measuredangle BAE=90°$ und die Strecke $[A E]$ , und dann den Winkel $\measuredangle AED=128°$ und die Strecke $[D E]$ .
Punkt $C$ ist durch $\overline{CE}=11\mathrm{\ cm}$ und $\overline{CD}=9\mathrm{\ cm}$ mit dem Zirkel konstruierbar.
(Alternativ kannst du auch mit dem Kosinussatz z.B. den Winkel $\measuredangle EDC$ berechnen und einzeichnen.)
Länge von $[B E]$ , Winkel $\measuredangle AEB$
Berechne die Länge der Strecke $[B E]$ und das Maß des Winkels $\measuredangle AEB$
Mit dem Satz des Pythagoras gilt im Dreieck $A B E$ :
Skizze
$\overline{BE} =\sqrt{\overline{AB}^2+\overline{AE}^2};\ \ \ \ \ \overline{BE}=\sqrt{{7}^2+{8}^2}\ cm$
$\overline{BE}=\ 10{,}63\ cm$
Im gleichen Dreieck kann mit dem Tangens der Winkel $\measuredangle AEB$ berechnet werden:
$\displaystyle\tan\measuredangle\mathrm{AEB}=\frac{\overline{AB}}{\overline{AE}};\ \ \ \ \ \ \ \ \ \ \ \tan\measuredangle\mathrm{AEB}=\frac{7}{8}$
$\measuredangle\mathrm{AEB}=41{,}19^{\circ}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne die Strecken unter den vorgegebenen Winkeln.
Konstruiere den Punkt $C$ mithilfe des Zirkels und verbinde das Fünfeck.
Berechne die Länge von $[B E]$ und das Maß von $\sphericalangle{AEB}$ im Dreieck $A B E$ .

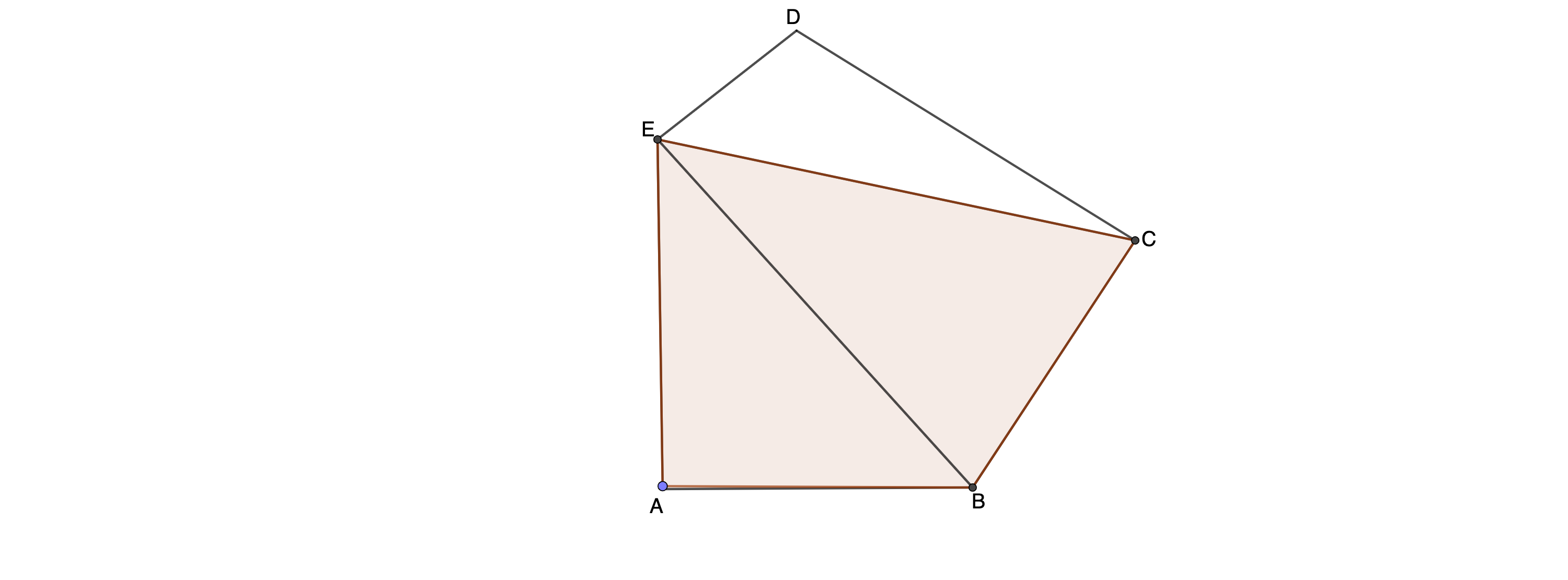
Ermitteln Sie durch Rechnung den Flächeninhalt des Vierecks $A B C E$ . (4 P)

$[$ Zwischenergebnis: $\sphericalangle{BEC}=36{,}33°]$

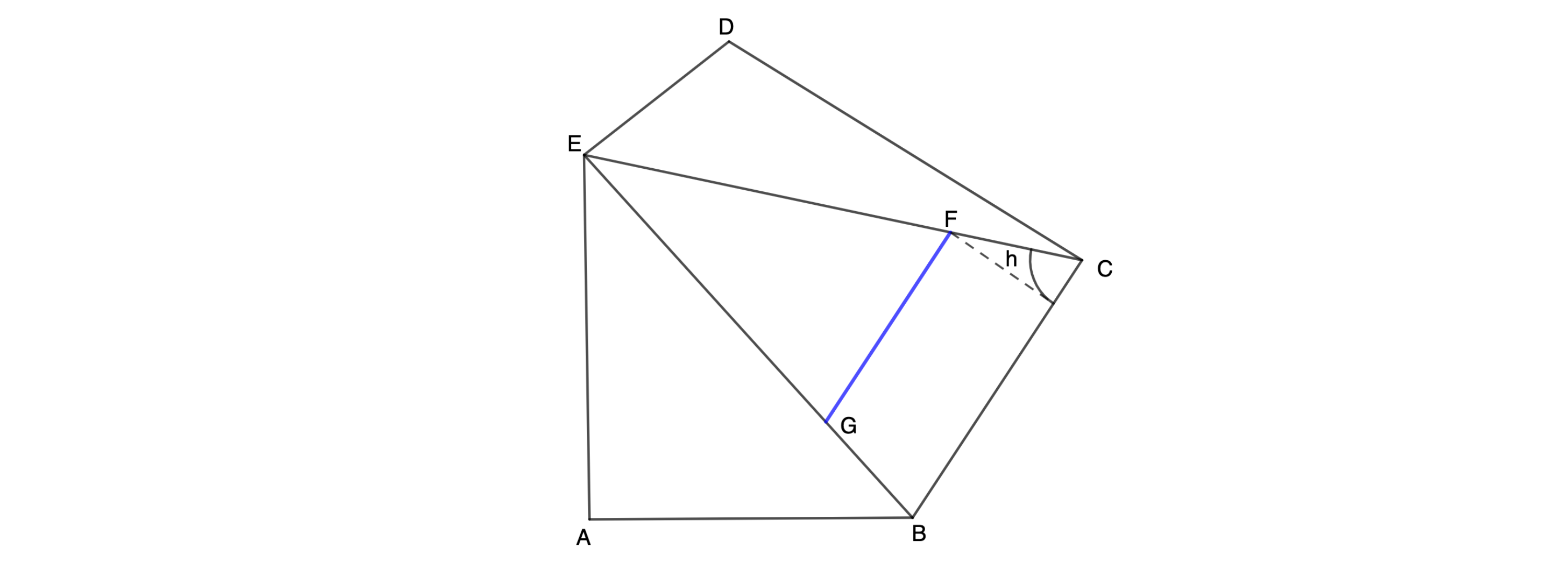
Zeigen Sie rechnerisch, dass für die Länge der Strecke $[B C]$ und das Maß des Winkels $E C B$ gilt: (2 P)
$\overline{BC}=6{,}75$ cm; $\sphericalangle{ECB}=68{,}90°$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Skizze
Berechnung der Länge von $[B C]$
Berechne die Strecke $B C$ mit Hilfe des Kosinussatzes.
$\overline{BC}^2=\overline{EB}^2+\overline{EC}^2-2\cdot\cos\sphericalangle{BEC}\cdot\overline{BE}\cdot\overline{CE}$
$\overline{BC}=\sqrt{\overline{EB}^2+\overline{EC}^2-2\cdot\cos\sphericalangle{BEC}\cdot\overline{BE}\cdot\overline{CE}}$
$\overline{BC}=\sqrt{\overline{EB}^2+\overline{EC}^2-2\cdot\cos\sphericalangle{BEC}\cdot\overline{BE}\cdot\overline{CE}}$
$\overline{BC}=\sqrt{11^2+10{,}63^2-2\cdot\cos36{,}33^{\circ}\cdot11\cdot10{,}63} \;\text{cm}$
$\overline{BC}=\sqrt{45{,}52}\,\text{cm}$
$\overline{BC}= 6{,}75\;\text{cm}$
Berechnung der Größe des Winkels $E C B$
Berechne den Winkel $E C B$ mit Hilfe des Sinussatzes.
$\dfrac{\sin36{,}33^\circ}{6{,}75\;\text{cm}}=\dfrac{\sin\sphericalangle{ECB}}{10{,}63\;\text{cm}}$
$\sin\sphericalangle{ECB}=\dfrac{\sin36{,}33^\circ\cdot10{,}63\;\text{cm}}{6{,}75\;\text{cm}}=0{,}933$
$\sphericalangle{ECB}\ =\ 68{,}90^\circ$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Länge von $[B C]$ mit dem Kosinussatz.
Verwende den Sinussatz für den Winkel $\sphericalangle{ECB}$ .
Die Punkte $F\in[CE]$ und $G\in[BE]$ legen die Strecke $[F G]$ fest, wobei gilt:
$[FG]\Vert[BC]$ und $\overline{CF}=3\;\text{cm}$ .
Ergänzen Sie die Strecke $[F G]$ in der Zeichnung zu 1a) und berechnen Sie den Flächeninhalt des Vierecks $B C F G$ . (4 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz
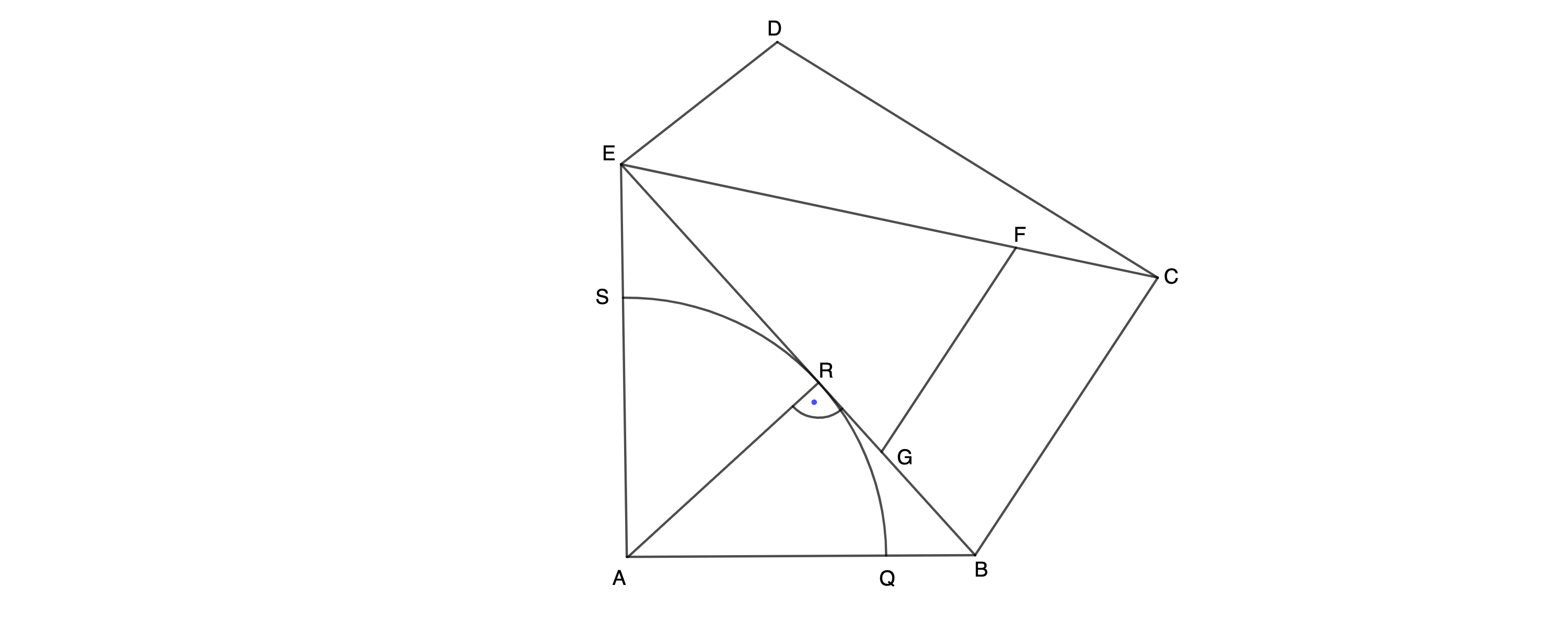
Skizze
Berechne den Flächeninhalt des Vierecks $B C F G$
Berechne zuerst mit Hilfe des Strahlensatzes die Länge der Strecke $[F G] .$
$\dfrac{\overline{FG}}{\overline{BC}}=\dfrac{\overline{EF}}{\overline{EC}}\ \ \Rightarrow\ \ \overline{FG}=\dfrac{\overline{BC}\cdot\overline{EF}}{\overline{EC}}$
$\overline{FG}=\dfrac{{6{,}75\;\text{cm}}\cdot{(11-3)\;\text{cm}}}{{11\;\text{cm}}}$
$\overline{FG}=4{,}91\;\text{cm}$
Höhe $h$ im Trapez $B C F G$
Berechne jetzt die Höhe $h$ mit dem Sinus:
$\dfrac{h}{3\;\text{cm}}=\sin68{,}90^\circ\Rightarrow\ h=3\;\text{cm}\cdot0{,}933$
$h=2{,}80\;\text{cm}$
Flächeninhalt des Trapezes
Das Viereck $B C F G$ ist ein Trapez. Die Formel zur Berechnung des Flächeninhaltes eines Trapezes lautet:
$A_{Trapez}= \dfrac{a+c}{2}\cdot{h}=\dfrac{\overline{BC}+\overline{FG}}{2}\cdot h$
$A_{BCFG}= \dfrac{6{,}75+4{,}91}{2}\cdot{2{,}80\;\text{cm}^2}$
$A_{BCFG}= 16{,}32\;\text{cm}^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne zuerst mit Hilfe des Strahlensatzes die Länge der Strecke $[F G] .$
Berechne dann die Höhe $h$ im Trapez $B C F G$ , sowie den Flächeninhalt.
Ein Kreis mit dem Mittelpunkt $A$ berührt die Strecke $[B E]$ im Punkt $R$ . Er schneidet die Strecke $[A B]$ im Punkt $Q$ und die Strecke $[A E]$ im Punkt $S$ .
Zeichnen Sie den Kreisbogen $\overset\frown{QS}$ und den Punkt $R$ in die Zeichnung zu 1a) ein.
Ermitteln Sie sodann rechnerisch den Flächeninhalt des Sektors, der von den Strecken $[A Q]$ und $[A S]$ sowie dem Kreisbogen $\overset\frown{QS}$ begrenzt wird. (3 P)
$[$ Zwischenergebnis: $\overline{AR}=5{,}27\;\text{cm}$ $]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreissektor
Skizze
Berechne den Flächeninhalt des Kreissektor $A Q S$ .
Um den Flächeninhalt des Kreissektors $A Q S$ zu berechnen, musst Du zuerst die Länge der Strecke $[A R]$ berechnen.
Der Winkel $AEB= 41{,}19^\circ$ .
$\dfrac{\overline{AR}}{\overline{AE}}=\sin\sphericalangle{AEB}\ \Rightarrow\overline{AR}=\overline{AE}\cdot\sin\sphericalangle{AEB}$ ; $\overline{AR}=8\;\text{cm}\cdot0{,}659$
$\overline{AR}= 5{,}27\;\text{cm}$
Berechne jetzt den Flächeninhalt des Kreissektor $A Q S$ .
$A_{Sektor}= \dfrac{\sphericalangle{BAE}}{{360^\circ}}\cdot\overline{AR^2}\cdot\large\pi$ ; $A_{Sektor}= \dfrac{90^\circ}{{360^\circ}}\cdot{27{,}77\;\text{cm}^2}\cdot\large\pi$
$A_{Sektor}=21{,}81\;\text{cm}^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Länge der Strecke $[A R]$ mit dem Sinus. Verwende hierzu, dass der Winkel $AEB= 41{,}19^\circ$ ist.
Bestimme mithilfe des Radius $[A R]$ den Flächeninhalt des Kreissektors.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B2
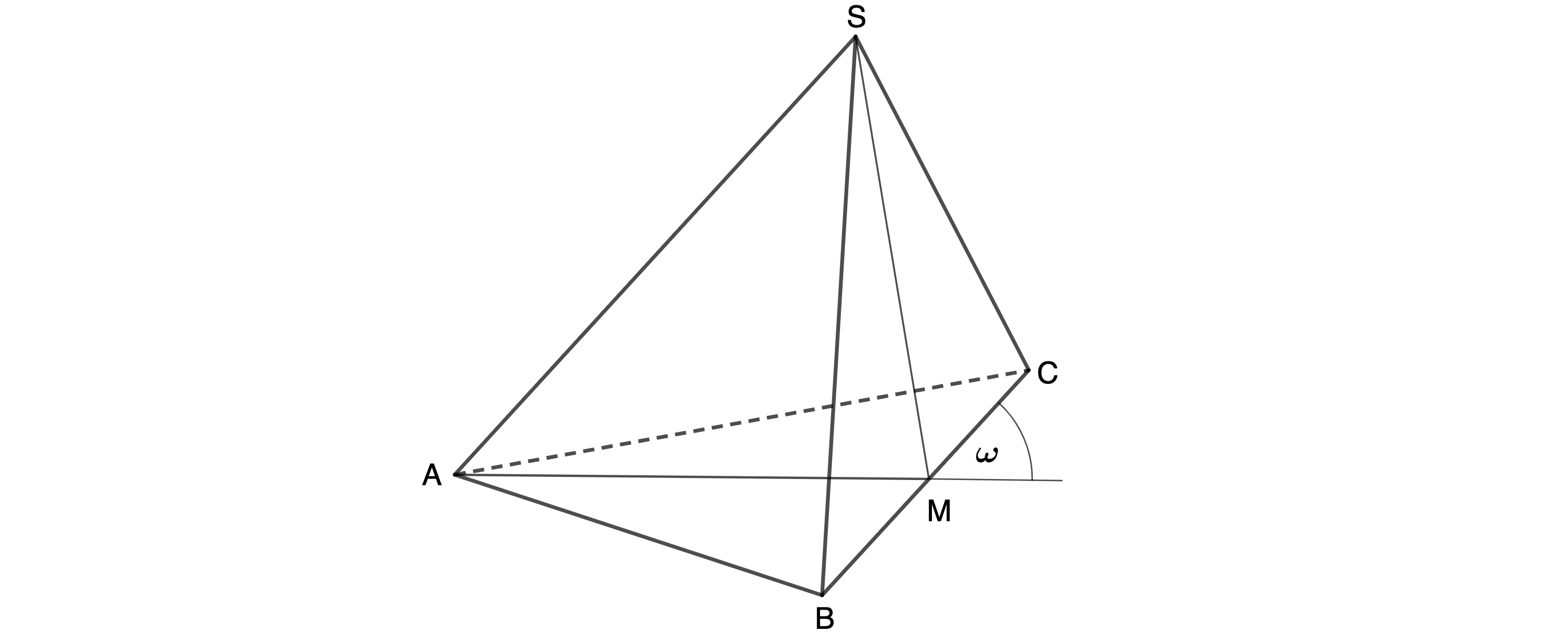
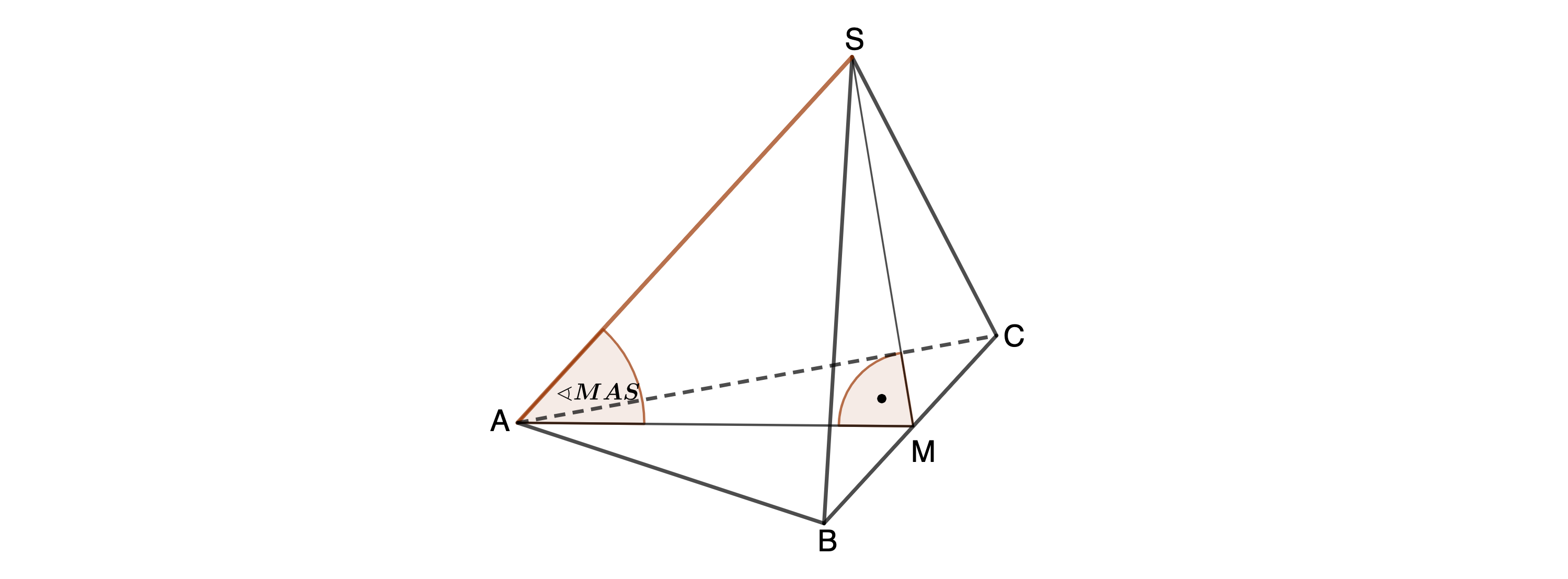
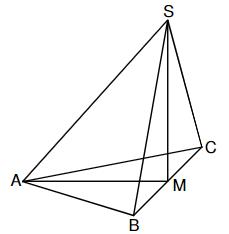
Die Skizze zeigt ein Schrägbild der Pyramide $A B C S$ mit der Höhe $[M S]$ , deren Grundfläche das gleichschenklige Dreieck $A B C$ ist. $M$ ist der Mittelpunkt der Basis $[B C]$ . Es gilt: $\overline{AM}=9$ cm; $\overline{BC}=12\;\text{cm}$ ; $\overline{MS}=10\;\text{cm}$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Zeichnen Sie das Schrägbild der Pyramide $A B C S$ , wobei die Strecke $[A M]$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $M$ liegen soll. Für die Zeichnung gilt: (2 P)
  $q = \dfrac{1}{2}$ ; $\omega= 45$ °.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
  Schrägbild zeichnen
  Zeichen zuerst die Schrägbildachse, die Strecke [ $A M$ ] liegt auf der Schrägbildachse. Trage die Strecke [ $B C$ ] in einem Winkel von $45^\circ$ zur Schrägbildachse an und vervollständige die Pyramide.
  Skizze
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere zuerst die Strecke $[A M]$ auf die Schrägbildachse.
  Zeichne die Strecke $[B C]$ in einem $45 °$ -Winkel dazu ein und vervollständige die Pyramide.
2. Berechnen Sie die Länge der Strecke $[A S]$ , das Maß des Winkels $M A S$ sowie das Volumen der Pyramide $A B C S$ . (3 P)
  $[$ Ergebnisse: $\overline{AS}=13{,}45$ ; $\sphericalangle{MAS}=48{,}01°$ ; $V_{ABCS}=180\;\text{cm}^3$ $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechtwinkliges Dreieck
  Berechne die Länge der Strecke $[A S]$ , das Maß des Winkels $M A S$ sowie das Volumen der Pyramide $A B C S$ .
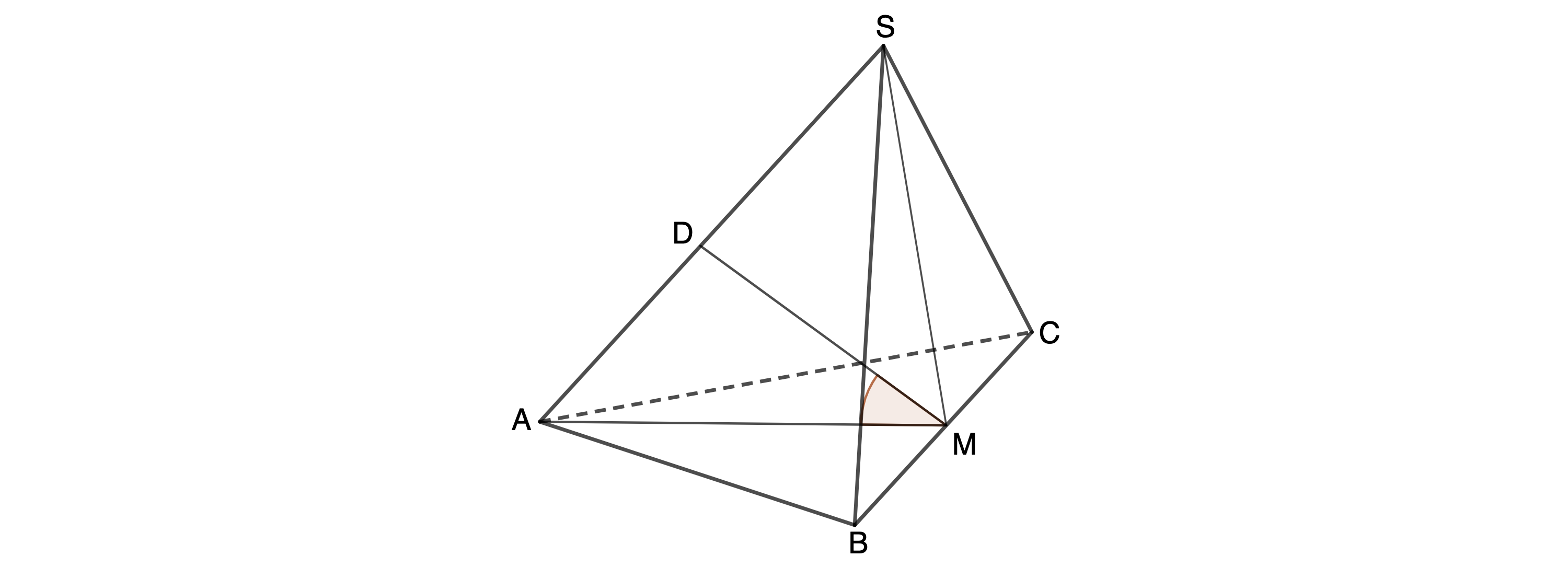
  Skizze des rechtwinkligen Dreiecks in der Pyramide
  Länge der Strecke $[A S]$
  Im rechtwinkligen Dreieck $A M S$ gilt mit dem Satz des Pythagoras:
  $\overline{AS}=\sqrt{\overline{AM^2}+\overline{MS^2}}=\sqrt{{9^2}+{10^2}}\;\text{cm}$
  $\overline{AS}=\sqrt{181}\;\text{cm}$
  $\overline{AS}= 13{,}45\;\text{cm}$
  Winkel $M A S$
  Mit dem Tangens gilt im rechtwinkligen Dreieck:
  $\tan\sphericalangle{MAS}=\dfrac{\overline{MS}}{\overline{MA}}\Rightarrow\tan\sphericalangle{MAS}=\dfrac{10\;\text{cm}}{9\;\text{cm}}$
  $\tan\sphericalangle{MAS}=1{,}1111$
  $\sphericalangle{MAS}=48{,}01^\circ$
  Volumen der Pyramide $A B C S$
  Mit der Formel für das Volumen einer Dreieckspyramide gilt:
  $V_{ABCS}=\dfrac{1}{3}\cdot{G}\cdot{h}$
  $V_{ABCS}=\dfrac{1}{3}\cdot{\dfrac{1}{2}\cdot\overline{BC}}\cdot\overline{AM}\cdot{\overline{MS}}\Rightarrow V_{ABCS}=\dfrac{1}{3}\cdot{\dfrac{1}{2}}\cdot{12}\cdot{9}\cdot{10}\;\text{cm}^3$
  $V_{ABCS}=180\;\text{cm}^3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Länge der Strecke $[A S]$ im Dreieck $A M S$ .
  Bestimme das Maß des Winkels $M A S$ mit dem Tangens im selben Dreieck.
  Berechne das Volumen der Pyramide. Achte darauf, dass das eine Pyramide mit dreieckiger Grundfläche ist.
3. Für den Punkt $D\in[AS]$ gilt: $\overline{AD}= 4\;\text{cm}$ .
  Zeichnen Sie die Strecke $[D M]$ in das Schrägbild zu 2a) ein und berechnen Sie das Maß des Winkels $D M A .$ (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
  Für den Punkt $D\in[AS]$ gilt: $\overline{AD}= 4\;\text{cm}$ .
  Zeichne die Strecke $[D M]$ in das Schrägbild zu 2a) ein und berechne das Maß des Winkels $D M A$ .
  Skizze
  Berechnung des Maßes des Winkels $D M A$
  Berechne zuerst die Länge der Strecke $[D M]$ .
  $\overline{DM}^2=\overline{AM}^2+\overline{AD}^2-2\cdot\cos\sphericalangle{MAS}\cdot\overline{AM}\cdot\overline{AD}$
  $\overline{DM}=\sqrt{{9}^2+{4}^2-2\cdot\cos48{,}01^\circ\cdot{9}\cdot{4}}\;\text{cm}$
  $\overline{DM}=\sqrt{81+16-{2}\cdot{9}\cdot{4}\cdot{0{,}669}}\;\text{cm}$
  $\overline{DM}=\sqrt{48{,}832}\;\text{cm}$
  $\overline{DM}=6{,}99\;\text{cm}$
  Berechne jetzt den Winkel $D M A$
  $\dfrac{\sin\sphericalangle{DMA}}{\overline{AD}}=\dfrac{\sin\sphericalangle{MAS}}{\overline{DM}}\Rightarrow\sin\sphericalangle{DMA}=\dfrac{\sin\sphericalangle{MAS}\cdot\overline{AD}}{\overline{DM}}$
  $\sin\sphericalangle{DMA}=\dfrac{{0{,}7433}\cdot{4\;\text{cm}}}{6{,}99\;\text{cm}}$
  $\sphericalangle{DMA}=25{,}17^\circ$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme das Maß des Winkels $D M A$ . Berechne hierzu zuerst die Länge der Strecke $[D M]$ .
4. Für Punkte $R_{n}$ auf der Strecke $[M S]$ gilt:
  $\overline{SR_n}= x\;\text{cm}$ , ( $x\in \mathbb{R}$ ; $0 \lt x \lt10$ ).
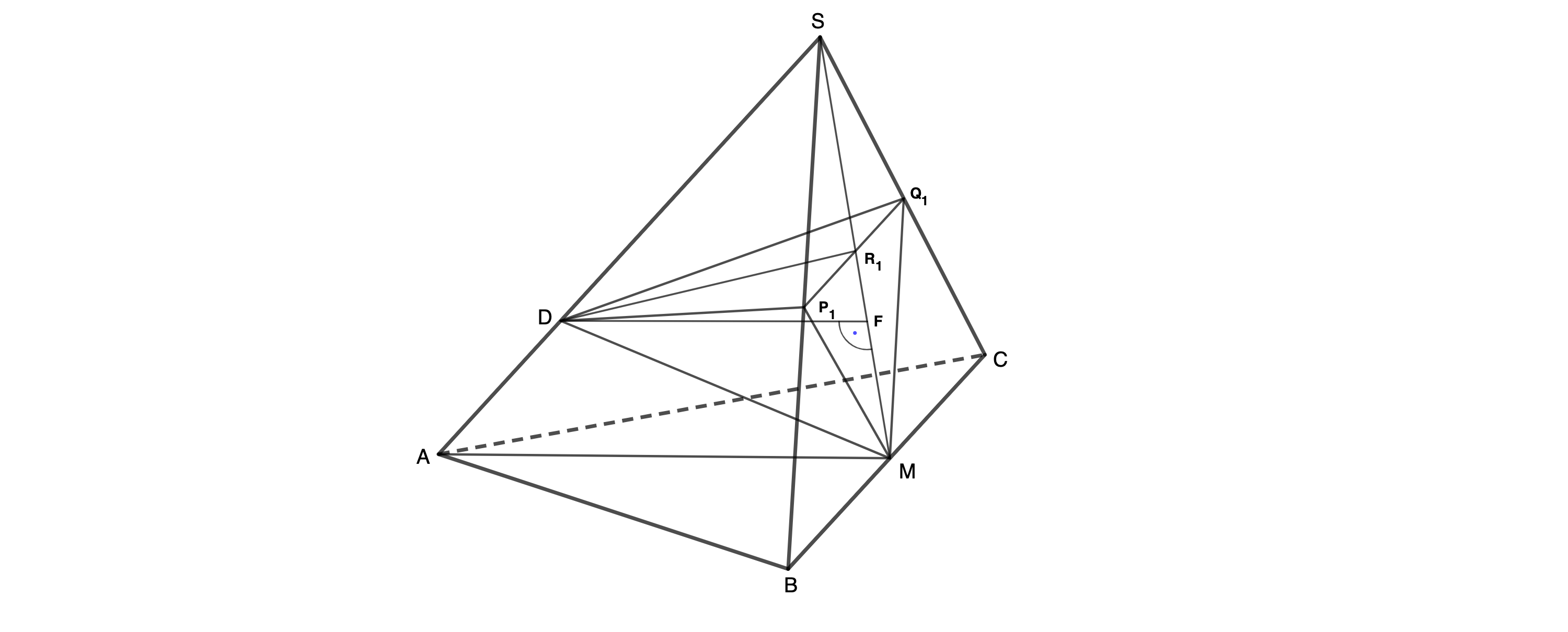
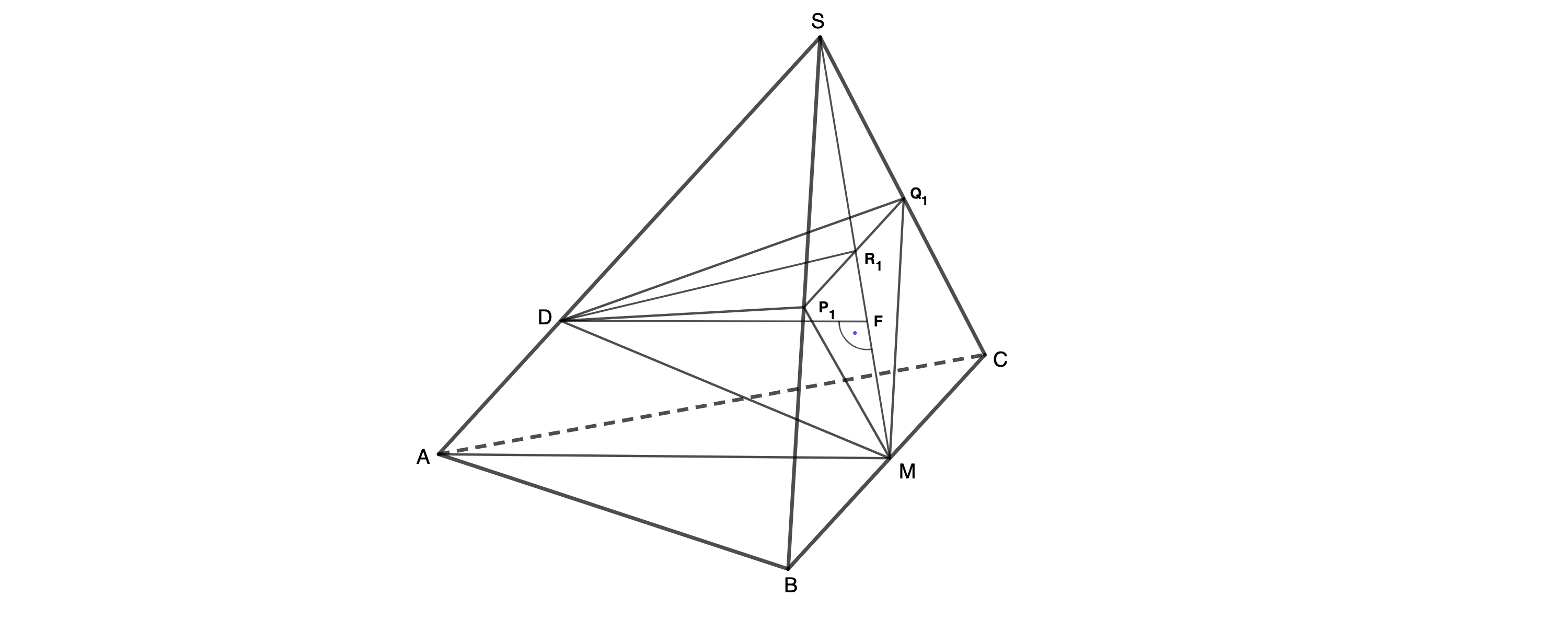
  Parallelen zur Strecke $[B C]$ durch die Punkte $R_{n}$ schneiden die Strecke $[B S]$ in den Punkten $P_{n}$ und die Strecke $[C S]$ in den Punkten $Q_{n}$ . Die Dreiecke $P_{n} M Q_{n}$ sind die Grundflächen von Pyramiden $P_{n} M Q_{n} D$ mit der Höhe $[D F]$ , wobei $F\in[MS]$ gilt.
  Zeichnen Sie die Pyramide $P_{1} M Q_{1} D$ und die Höhe $[D F]$ für $x = 5$ in das Schrägbild zu 2a) ein. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Skizze der Pyramide
  Für Punkte $R_{n}$ auf der Strecke $[M S]$ gilt:
  $\overline{SR_n}= x\;\text{cm}$ , ( $x\in \mathbb{R}$ ; $0 \lt x \lt10$ ).
  Parallelen zur Strecke $[B C]$ durch die Punkte $R_{n}$ schneiden die Strecke $[B S]$ in den Punkten $P_{n}$ und die Strecke $[C S]$ in den Punkten $Q_{n}$ . Die Dreiecke $P_{n} M Q_{n}$ sind die Grundflächen von Pyramiden $P_{n} M Q_{n} D$ mit der Höhe $[D F]$ , wobei $F\in[MS]$ gilt.
  Zeichne die Pyramide $P_{1} M Q_{1} D$ und die Höhe $[D F]$ für $x = 5$ in das Schrägbild zu 2a) ein.
  Skizze
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere die Punkte $R_{n}$ , $P_{n}$ und $Q_{n}$ für $x = 5$ in das Dreieck $B C S$ der Pyramide. Vervollständige diese Punkte zu einer Pyramide.
  Die Spitze der inneren Pyramide ist durch $D$ auf der Strecke $[A S]$ gegeben.
5. Zeigen Sie rechnerisch, dass für das Volumen $V$ der Pyramiden $P_{n} M Q_{n} D$ in Abhängigkeit von x gilt: $V(x)=(-1{,}26x^2+12{,}64x)\;\text{cm}^3$ . (4 P)
  $[$ Zwischenergebnis: $\overline{DF}=6{,}32\;\text{cm}$ $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Zeige rechnerisch, dass für das Volumen $V$ der Pyramiden $P_{n} M Q_{n} D$ in Abhängigkeit von x gilt: $V(x)=(-1{,}26x^2+12{,}64x)\;\text{cm}^3$ .
  Skizze
  Berechnung von $\overline{DF}$ (die Höhe)
  Mit dem Strahlensatz gilt:
  $\dfrac{\overline{DF}}{\overline{AM}}=\dfrac{\overline{AS}-\overline{AD}}{\overline{AS}}\ \Rightarrow\ \overline{DF}=\dfrac{\overline{AM}\cdot(\overline{AS}-\overline{AD})}{\overline{AS}}$
  $\overline{DF}=\dfrac{{9}\cdot({13{,}45}-{4})}{{13{,}45}}\;\text{cm}$
  $\overline{DF}=6{,}32\;\text{cm}$
  Berechnung des Volumens
  $V{(x)}=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot\overline{P_{n}Q_{n}}\cdot\overline{MR_{n}}\cdot\overline{DF}$
  Berechne $\ \overline{P_{n}Q_{n}}$ mithilfe des Strahlensatzes:
  $\dfrac{\overline{P_{n}Q_{n}}(x)}{12\;\text{cm}}=\dfrac{x\ cm}{10\;\text{cm}}\ \Rightarrow\overline{P_{n}Q_{n}}(x)= \dfrac{12 \cdot\ x}{10}\;\text{cm}$
  $\overline{P_{n}Q_{n}}(x)=1{,}2\cdot{x}\;\text{cm}$
  $V{(x)}=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot1{,}2\cdot{x}\cdot(10-x)\cdot6{,}32\;\text{cm}^3$
  $V{(x)}=0{,}2\cdot{x}\cdot(63{,}2-6{,}32x)\;\text{cm}^3$
  $V{(x)}=(-1{,}26x^2+12{,}64x)\;\text{cm}^3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Höhe der inneren Pyramide $\overline{DF}$ mit dem Strahlensatz.
  Bestimme das Volumen der inneren Pyramide mit der dreieckigen Grundfläche.
  Die Länge der Seite $P_{n} Q_{n}$ kann auch mit dem Strahlensatz berechnet werden.
6. Es gibt Pyramiden $P_{2} M Q_{2} D$ und $P_{3} M Q_{3} D$ , deren Volumen jeweils um $90 %$ kleiner ist als das Volumen der Pyramide $A B C S$ .
  Berechnen Sie die zugehörigen x-Werte. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
  Es gibt Pyramiden $P_{2} M Q_{2} D$ und $P_{3} M Q_{3} D$ , deren Volumen jeweils um $90 %$ kleiner ist als das Volumen der Pyramide $A B C S$ . Berechne die zugehörigen x-Werte.
  Bestimmung der Volumina
  Das Volumen der Pyramide $ABCS=180\;\text{cm}^3$
  Das Volumen der Pyramiden $P_{2} M Q_{2} D$ und $P_{3} M Q_{3} D$ ist also $180\;\text{cm}^3\cdot 0{,}1=18\;\text{cm}^3$ .
  Lösen nach $x$
  Löse die quadratische Gleichung (die mit dem Term aus Teilaufgabe (e) gegeben ist):
  $-1{,}26x^2+12{,}64x=180\cdot{0{,}1}$
  $-1{,}26x^2+12{,}64x-18=0$
  $x_{1{,}2}=\dfrac{-12{,}64\ \pm\ \sqrt{12{,}64^2\ -\ 4\cdot(-1{,}26)\cdot(-18)}}{2\cdot(-1{,}26)}$
  $x_{1}=1{,}72;\ \ x_{2}=8{,}31$
  $\mathbb{L}=\left\{1{,}72;\ 8{,}31\right\}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne, wie groß das Zehntel des Volumens von $A B C S$ ist.
  Setze diesen Wert gleich mit dem Term für das Volumen aus Teilaufgabe (e). -
  Löse diese quadratische Gleichung.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \large{A}_{BCE}$	$=$	$\displaystyle \dfrac12\cdot a\cdot b\cdot\sin\gamma$
	$=$	$\displaystyle \dfrac{1}{2}\cdot11\cdot10{,}63\cdot\sin36{,}33^\circ$
	$\approx ≈$	$\displaystyle 34{,}64\;\text{cm}^2$

Teil B

Aufgabe B1

Zeichnen des Fünfecks

Länge von [BE][BE][BE], Winkel ∡AEB\measuredangle AEB∡AEB

Hast du eine Frage oder Feedback?

Flächeninhalt des Vierecks

Hast du eine Frage oder Feedback?

Berechnung der Länge von [BC][BC][BC]

Berechnung der Größe des Winkels ECBECBECB

Hast du eine Frage oder Feedback?

Berechne den Flächeninhalt des Vierecks BCFGBCFGBCFG

Höhe hhh im Trapez BCFGBCFGBCFG

Flächeninhalt des Trapezes

Hast du eine Frage oder Feedback?

Berechne den Flächeninhalt des Kreissektor AQSAQSAQS.

Hast du eine Frage oder Feedback?

Aufgabe B2

Schrägbild zeichnen

Hast du eine Frage oder Feedback?

Länge der Strecke [AS][AS][AS]

Winkel MASMASMAS

Volumen der Pyramide ABCSABCSABCS

Hast du eine Frage oder Feedback?

Berechnung des Maßes des Winkels DMADMADMA

Hast du eine Frage oder Feedback?

Skizze der Pyramide

Hast du eine Frage oder Feedback?

Berechnung von DF‾\overline{DF}DF (die Höhe)

Berechnung des Volumens

Hast du eine Frage oder Feedback?

Bestimmung der Volumina

Lösen nach xxx

Hast du eine Frage oder Feedback?

Länge von $[B E]$ , Winkel $\measuredangle AEB$

Berechnung der Länge von $[B C]$

Berechnung der Größe des Winkels $E C B$

Berechne den Flächeninhalt des Vierecks $B C F G$

Höhe $h$ im Trapez $B C F G$

Berechne den Flächeninhalt des Kreissektor $A Q S$ .

Länge der Strecke $[A S]$

Winkel $M A S$

Volumen der Pyramide $A B C S$

Berechnung des Maßes des Winkels $D M A$

Berechnung von $\overline{DF}$ (die Höhe)

Lösen nach $x$