Inhalt des Kurses

In diesem Kurs lernst du, wie man Brüche addiert und subtrahiert.

Vorkenntnisse

Du solltest wissen, was Brüche sind und wie man erweitert und kürzt.

Kursdauer

Dieser Kurs dauert ca. 30-35 Minuten.

Brüche erweitern - ein Beispiel

Erweitere den Bruch $\frac{3}{4}\backslash frac\{3\}\{4\}$ auf Zwölftel.

Brüche kürzen - ein Beispiel

Kürze den Bruch $\frac{24}{36}\backslash frac\{24\}\{36\}$ so weit wie möglich.

Solltest du nochmal ausführlich das Thema "Brüche kürzen und erweitern" wiederholen wollen, klicke hier. Oder du übst passende Aufgaben zum Erweitern oder Kürzen.

Happy Birthday

Jan hat Geburtstag, es gibt Zitronenkuchen

Wenn wir uns diesen genauer ansehen, liegen dort $22$ Stücke. Da der Kuchen in $88$ gleich große Teile geschnitten wurde, ist jedes Stück $\frac{1}{8}\backslash frac\{1\}\{8\}$ Blech groß.

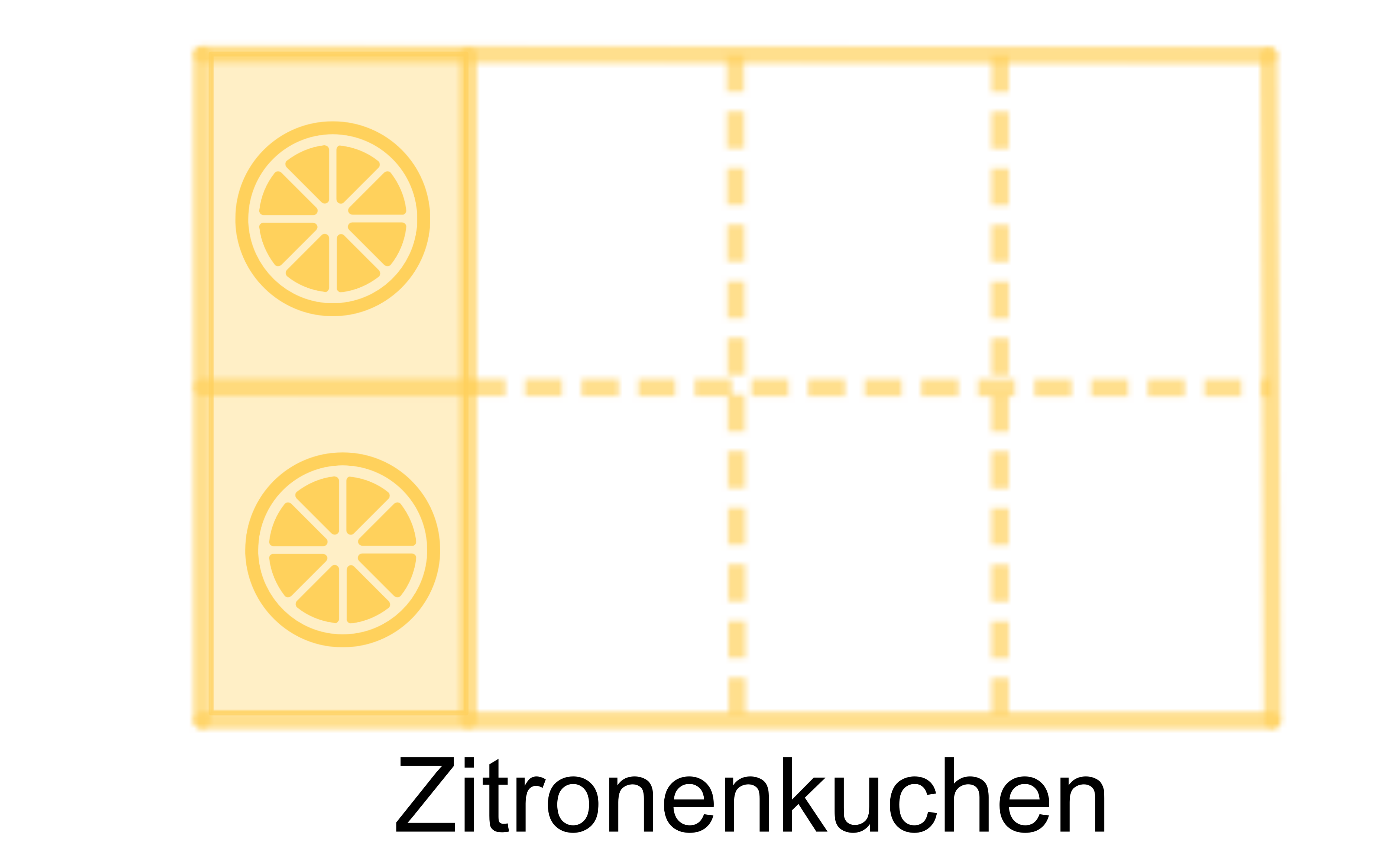
Insgesamt sind also $\frac{1}{8}+\frac{1}{8}\backslash frac\{1\}\{8\}+\backslash frac\{1\}\{8\}$ Bleche Zitronenkuchen noch da. Diese sind zusammen $\frac{2}{8}\backslash frac\{2\}\{8\}$ Bleche groß,

Wir sehen also, dass bei der Addition gleichnamiger Brüche die Zähler addiert werden, während der Nenner gleich bleibt.

Schokolade

Da so wenig vom Zitronenkuchen übrig ist, kauft Jan Schokolade für einen Marmorkuchen. Seine Freunde Tim & Tom zerteilen die Schokolade in $1212$ gleich große Stücke.

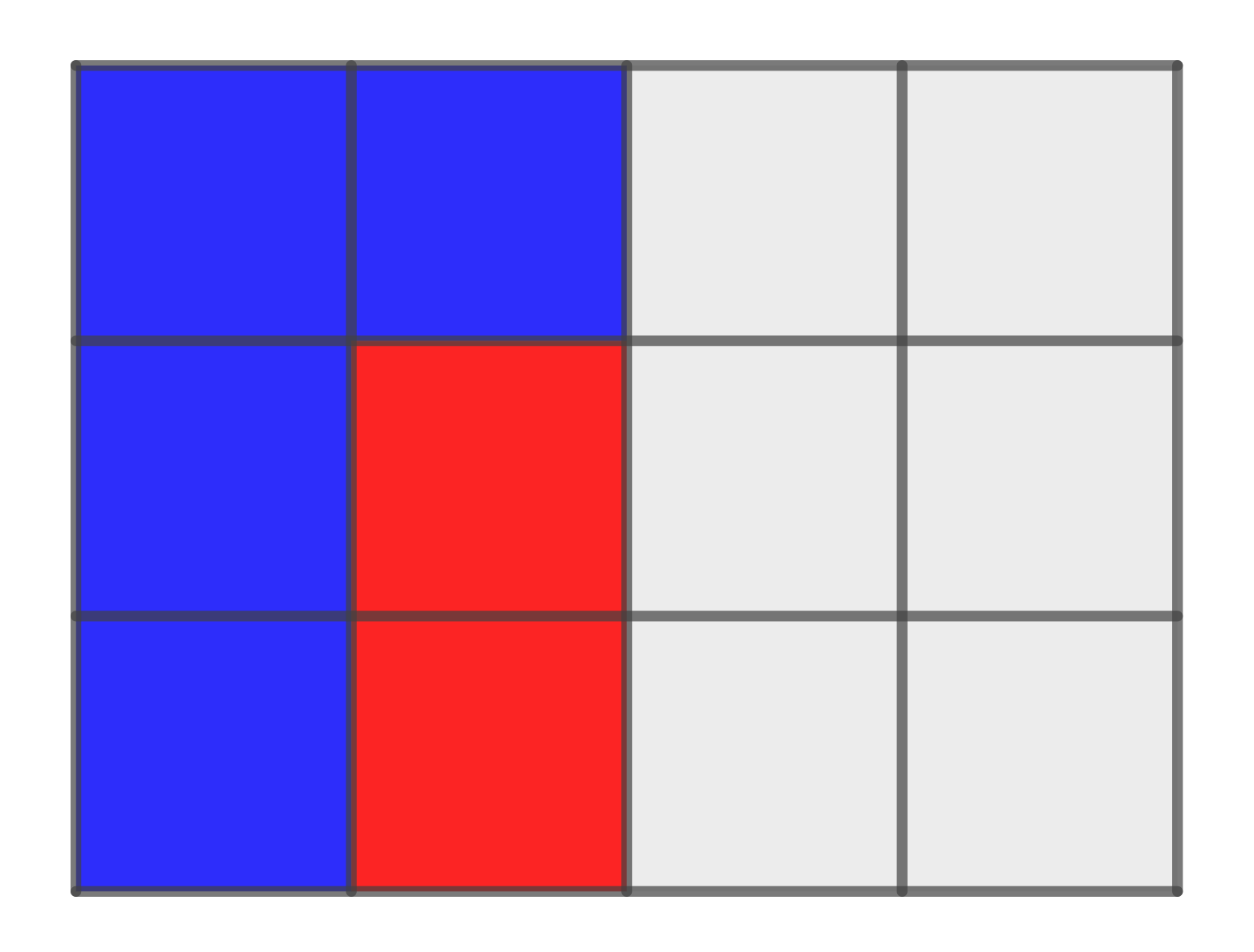
Wie viele Stücke essen Tim (blau) & Tom (rot)?

Welcher Bruchteil der Schokoladentafel bleibt nun für den Kuchen übrig?

Wie auch in der Grafik zu sehen, bleiben $12-6=612-6=6$ Stücke übrig, also der Bruchteil $\frac{6}{12}\backslash frac\{6\}\{12\}$. Dahinter steht die Rechnung

Wir sehen also, dass bei der Subtraktion gleichnamiger Brüche die Zähler subtrahiert werden, während der Nenner gleich bleibt.

Übungsaufgabe

Nach der Party

Nach der Party ist nur noch wenig übrig: ein Stück Marmor- und zwei Stücke Zitronenkuchen. Doch werden Jans Eltern noch satt?

Brüche mit unterschiedlichen Nennern müssen erst auf einen gemeinsamen Nenner gebracht werden. Dafür muss der Bruch auf ein gemeinsames Vielfaches der Nenner erweitert werden.

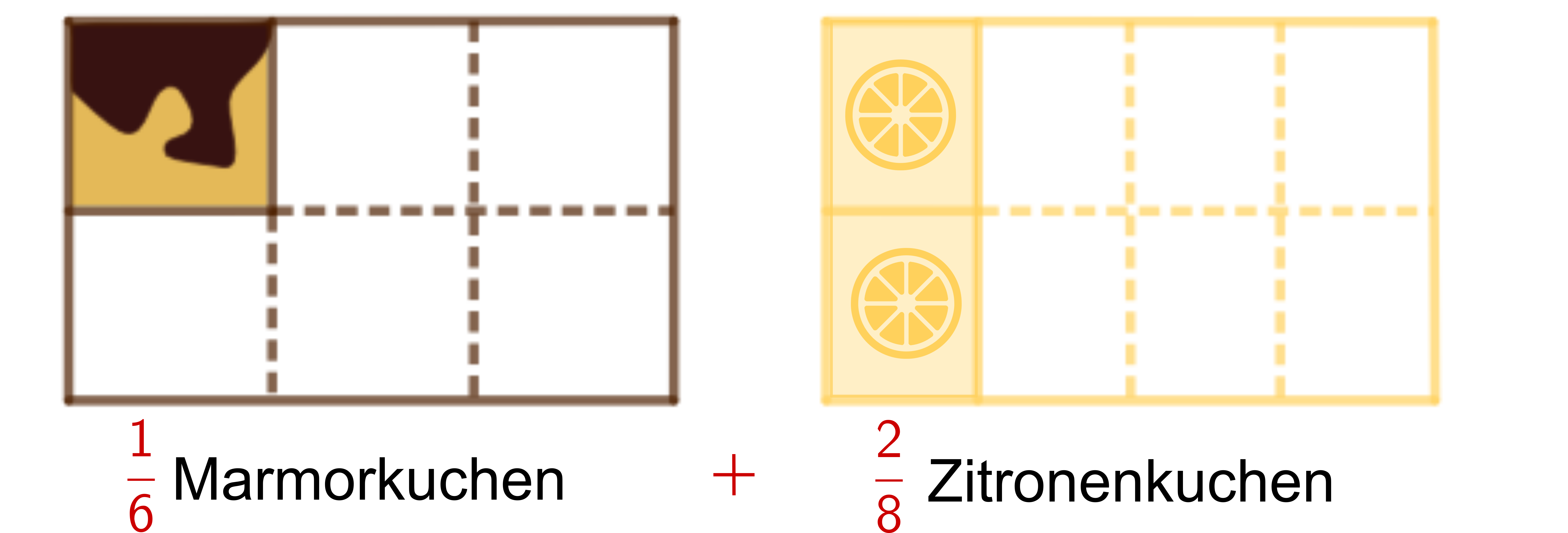
Wir teilen die Kuchen in gleich große Stücke. Um das zu machen, brauchen wir ein gemeinsames Vielfaches der Nenner 6 und 8, also beispielsweise 24.

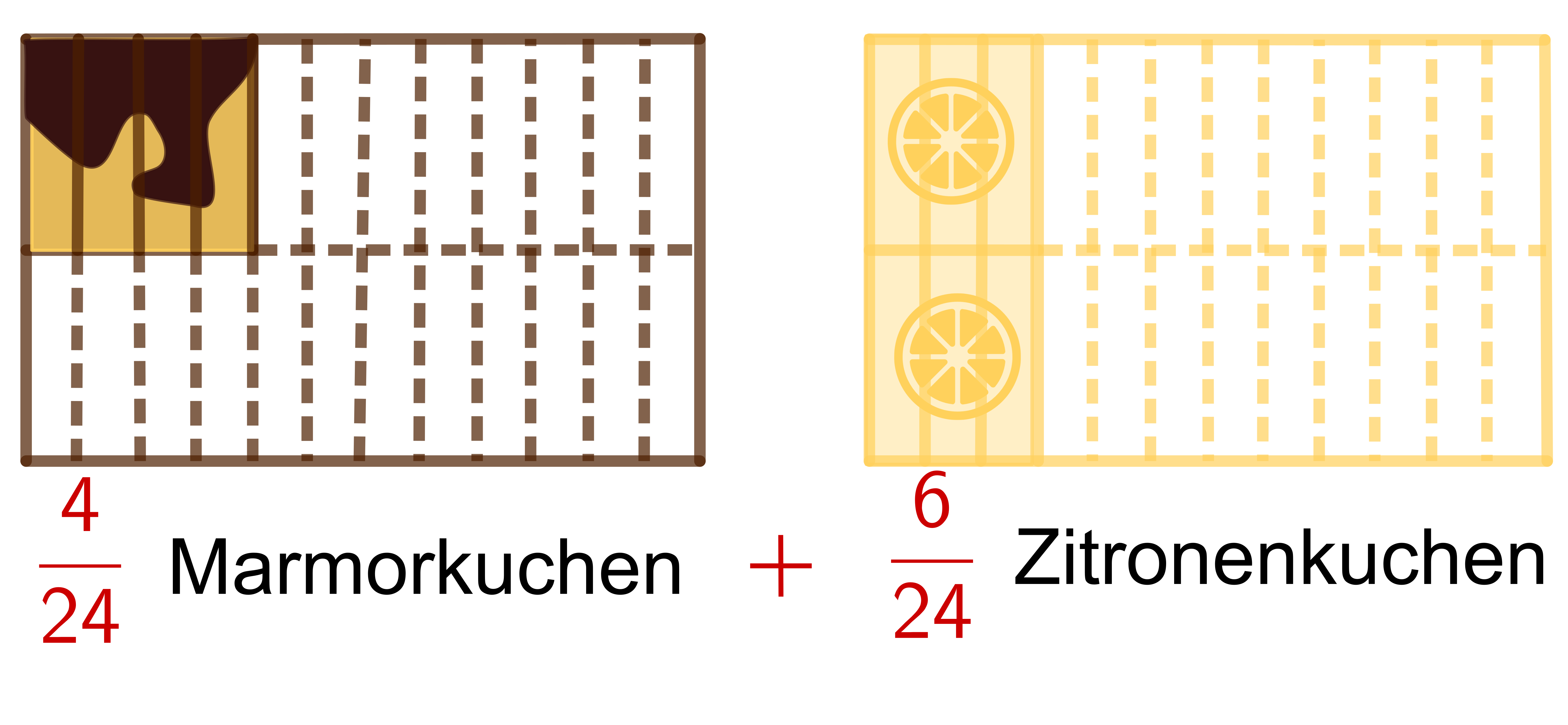
Nun haben wir gleich große Kuchenstücke, die wir problemlos in ein Blech zusammensetzen und abzählen können.

Übungsaufgaben:

Bilde die Summe aus $\frac{1}{3}\backslash frac\{1\}\{3\}$ und $\frac{1}{2}\backslash frac\{1\}\{2\}$.

Subtrahiere $\frac{1}{3}\backslash frac\{1\}\{3\}$ von $\frac{1}{2}\backslash frac\{1\}\{2\}$