Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Lagebeziehung Punkt-Dreieck (Inzidenz)

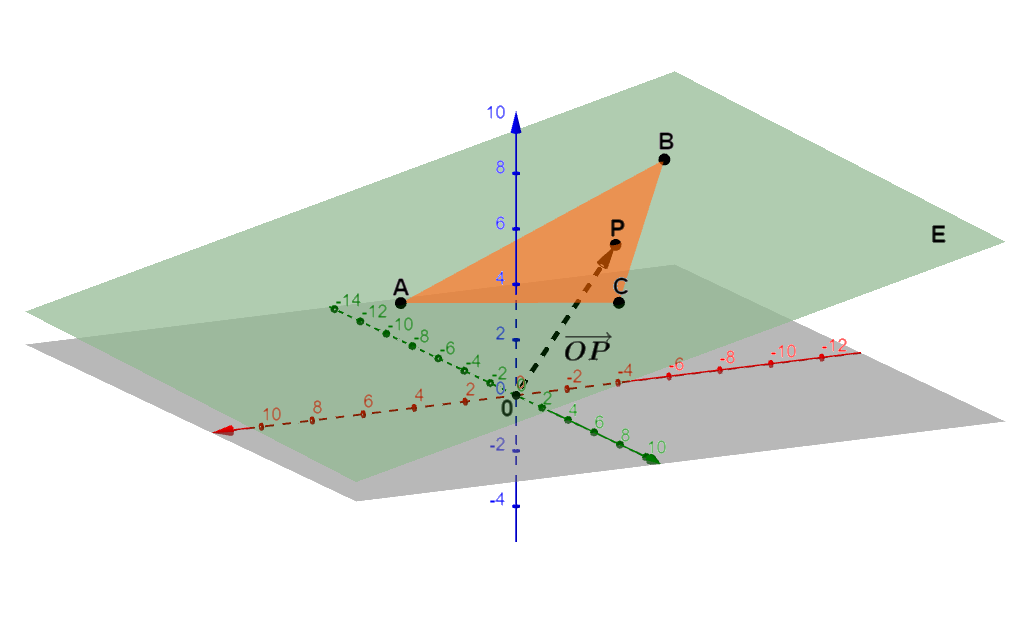
Aus drei Punkten AA, BB und CC, die nicht auf einer Geraden liegen, kann ein Dreieck im Raum gebildet werden.

Die drei Punkte liegen in einer Ebene EABCE_{ABC}.

EABC:  X⃗=OA→+r⋅AB→+s⋅AC→E_{ABC}:\;\vec X=\overrightarrow{OA}+r\cdot \overrightarrow{AB} +s\cdot \overrightarrow{AC}

Wann liegt ein beliebiger Punkt PP im Dreieck?

Der Punkt PP liegt dann im Dreieck, wenn drei Bedingungen erfüllt sind:

I.    P∈EABC\mathrm{I.}\;\;P\in E_{ABC}

II.    0≤r,s≤1\mathrm{II.}\;\;0\leq r,s\leq 1

III.  0≤r+s≤1\mathrm{III.}\;0\leq r+s\leq 1

Punkt im Dreieck

Vorgehensweise

Von einem Dreieck sind die Punkte AA, BB und CC gegeben und ein weiterer Punkt PP. Erstelle mit den 33 Punkten die Parameterform der Ebenengleichung.

EABC:  X⃗=OA→+r⋅AB→+s⋅AC→\displaystyle E_{ABC}:\;\vec X=\overrightarrow{OA}+r\cdot \overrightarrow{AB} +s\cdot \overrightarrow{AC}

Führe eine Punktprobe durch:

Setze für X⃗\vec X den Vektor OP→\overrightarrow{OP} ein:

OP→=OA→+r⋅AB→+s⋅AC→\displaystyle \overrightarrow{OP}=\overrightarrow{OA}+r\cdot\overrightarrow{AB}+s\cdot\overrightarrow{AC}

Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.

  • Fall 1: Das Gleichungssystem hat eine Lösung, d.h. es gibt Werte für die Parameter rr und ss. Dann ist die Bedingung I.  P∈EABC\mathrm{I.}\;P\in E_{ABC} ist erfüllt, der Punkt PP liegt in der Ebene EABCE_{ABC}.

  • Fall 1 a): Die berechneten Parameterwerte erfüllen auch die oben genannten Bedingungen II.\mathrm{II.} und III.\mathrm{III.} Dann liegt der Punkt PP im Dreieck.

  • Fall 1 b): Eine (oder beide) der Bedingungen II.\mathrm{II.} oder III.\mathrm{III.} ist nicht erfüllt. Dann liegt der Punkt zwar in der Ebene durch AA, BB und CC, aber nicht im Dreieck.

  • Fall 2: Das Gleichungssystem hat keine Lösung. Dann liegt der Punkt PP nicht in der Ebene EABCE_{ABC} und auch nicht im Dreieck.

Beispiel der Punkt P liegt im Dreieck

Gegeben sind die Punkte A(1∣2∣2)A(1|2|2), B(3∣1∣4)B(3|1|4) und C(−2∣1∣1)C(-2|1|1) und der Punkt P(0∣54∣2)P(0|\frac{5}{4}|2). Liegt der Punkt PP in dem Dreieck ABCABC?

Erstelle mit den 33 Punkten die Parameterform der Ebenengleichung.

EABC:  X⃗=(122)+r⋅(2−12)+s⋅(−3−1−1)E_{ABC}:\;\vec X=\begin{pmatrix}1 \\ 2 \\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ -1 \\ -1 \end{pmatrix}

Führe eine Punktprobe durch. Setze für X⃗\vec X den Vektor OP→\overrightarrow{OP} ein:

(0542)=(122)+r⋅(2−12)+s⋅(−3−1−1)  ⇒  (−1−340)=r⋅(2−12)+s⋅(−3−1−1)\begin{pmatrix}0 \\ \frac{5}{4} \\ 2 \end{pmatrix}=\begin{pmatrix}1 \\ 2 \\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ -1 \\ -1 \end{pmatrix}\;\Rightarrow\;\begin{pmatrix}-1 \\ -\frac{3}{4} \\ 0 \end{pmatrix}=r\cdot \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ -1 \\ -1 \end{pmatrix}

Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.

(I):    −1=2⋅r−3⋅s(II):−34=−1⋅r−1⋅s(III):0=2⋅r−1⋅s\def\arraystretch{1.25} \begin{array}{rrrrrcrr}&\mathrm{(I)}:&\;\;&-1&=&2\cdot r&-&3\cdot s\\&\mathrm{(II)}:& &-\frac{3}{4}&=&-1\cdot r&-&1 \cdot s\\&\mathrm{(III)}:& &0&=&2\cdot r&-&1 \cdot s\end{array}

Dieses Gleichungssystem kannst du z.B. mit dem Additionsverfahren lösen.

Rechne z.B. (I)−(III):  −1=−2s  ⇒  s=12 \mathrm{(I)}-\mathrm{(III)}:\;-1=-2s\;\Rightarrow\;s=\dfrac{1}{2}

Aus Gleichung (III)  \mathrm{(III)}\;folgt: 0=2⋅r−12  ⇒  r=14 0=2\cdot r-\dfrac{1}{2}\;\Rightarrow\;r=\dfrac{1}{4}

Probe in Gleichung (II):  −34=−14−12=−34  ✓ \mathrm{(II)}:\;-\dfrac{3}{4}=-\dfrac{1}{4}-\dfrac{1}{2}=-\dfrac{3}{4}\;\checkmark

Du hast bei der Lösung des Gleichungssystems die Werte r=14r=\dfrac{1}{4} und s=12s=\dfrac{1}{2} erhalten.

Das Gleichungssystem hat eine Lösung, d.h. die Bedingung I.  P∈EABC\mathrm{I.}\;P\in E_{ABC} ist erfüllt. Der Punkt PP liegt in der Ebene EABCE_{ABC}. Die beiden Parameter müssen die Bedingungen II.\mathrm{II.} und III.\mathrm{III.} erfüllen, damit der Punkt PP im Dreieck liegt.

II.    0≤r,s≤1\displaystyle \mathrm{II.}\;\;0\leq r,s\leq 1

Die Bedingung II. \mathrm{II.} ist erfüllt. Beide Parameterwerte sind größer gleich 00 und kleiner gleich 11.

Die Bedingung III.\mathrm{III.} ist auch erfüllt.

III.  0≤14+12≤1  ⇒  0≤34≤1  ✓\displaystyle \mathrm{III.}\;0\leq \dfrac{1}{4}+\dfrac{1}{2}\leq 1\;\Rightarrow\;0\leq \dfrac{3}{4}\leq 1\;\checkmark

Ergebnis: Der Punkt PP liegt im Dreieck.

Beispiel der Punkt P liegt nicht im Dreieck

Gegeben sind die Punkte A(1∣2∣2)A(1|2|2), B(3∣1∣4)B(3|1|4) und C(−2∣1∣1)C(-2|1|1) und der Punkt P(−14∣34∣94)P(-\frac{1}{4}|\frac{3}{4}|\frac{9}{4}). Liegt der Punkt PP in dem Dreieck ABCABC?

Erstelle mit diesen 33 Punkten die Parameterform der Ebenengleichung.

EABC:  X⃗=(122)+r⋅(2−12)+s⋅(−3−1−1)\displaystyle E_{ABC}:\;\vec X=\begin{pmatrix}1 \\ 2 \\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ -1 \\ -1 \end{pmatrix}

Führe eine Punktprobe durch. Setze für X⃗\vec X den Vektor OP→\overrightarrow{OP} ein:

(−143494)=(122)+r⋅(2−12)+s⋅(−3−1−1)  ⇒  (−54−5414)=r⋅(2−12)+s⋅(−3−1−1)\displaystyle \begin{pmatrix}-\frac{1}{4} \\[1ex] \frac{3}{4} \\[1ex] \frac{9}{4} \end{pmatrix}=\begin{pmatrix}1 \\ 2 \\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ -1 \\ -1 \end{pmatrix}\;\Rightarrow\;\begin{pmatrix}-\frac{5}{4} \\[1ex] -\frac{5}{4} \\[1ex] \frac{1}{4} \end{pmatrix}=r\cdot \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ -1 \\ -1 \end{pmatrix}

Du hast ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten erhalten.

(I):    −54=2⋅r−3⋅s(II):−54=−1⋅r−1⋅s(III):14=2⋅r−1⋅s\def\arraystretch{1.25} \begin{array}{rrrrrcrr}&\mathrm{(I)}:&\;\;&-\frac{5}{4}&=&2\cdot r&-&3\cdot s\\&\mathrm{(II)}:& &-\frac{5}{4}&=&-1\cdot r&-&1 \cdot s\\&\mathrm{(III)}:& &\frac{1}{4}&=&2\cdot r&-&1 \cdot s\end{array}

Dieses Gleichungssystem kannst du z.B. mit dem Additionsverfahren lösen.

Rechne z.B. (I)−(III):  −64=−2s  ⇒  s=34 \mathrm{(I)}-\mathrm{(III)}:\;-\dfrac{6}{4}=-2s\;\Rightarrow\;s=\dfrac{3}{4}

Aus Gleichung (III)  \mathrm{(III)}\;folgt: 14=2⋅r−34  ⇒  r=12 \dfrac{1}{4}=2\cdot r-\dfrac{3}{4}\;\Rightarrow\;r=\dfrac{1}{2}

Probe in Gleichung (II):  −54=−12−34=−54  ✓ \mathrm{(II)}:\;-\dfrac{5}{4}=-\dfrac{1}{2}-\dfrac{3}{4}=-\dfrac{5}{4}\;\checkmark

Du hast bei der Lösung des Gleichungssystems die Werte r=12r=\dfrac{1}{2} und s=34s=\dfrac{3}{4} erhalten.

Das Gleichungssystem hat eine Lösung, d.h. die Bedingung I.  P∈EABC\mathrm{I.}\;P\in E_{ABC} ist erfüllt. Der Punkt PP liegt in der Ebene EABCE_{ABC}. Die beiden Parameter müssen die Bedingungen II.\mathrm{II.} und III.\mathrm{III.} erfüllen, damit der Punkt PP im Dreieck liegt.

II.    0≤r,s≤1\displaystyle \mathrm{II.}\;\;0\leq r,s\leq 1

Die Bedingung II. \mathrm{II.} ist erfüllt. Beide Parameterwerte sind größer gleich 00 und kleiner gleich 11.

Die Bedingung III.\mathrm{III.} ist nicht erfüllt.

III.  0≤12+34≤1  ⇒  r+s=54\displaystyle \mathrm{III.}\;0\leq \dfrac{1}{2}+\dfrac{3}{4}\leq 1\;\Rightarrow\;r+s=\dfrac{5}{4}

und somit ist 54≥1\frac{5}{4}\ge1.

Ergebnis: Der Punkt PP liegt zwar in der Ebene EABCE_{ABC}, in der sich das Dreieck befindet, aber nicht im Dreieck.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?