1 Was werden wir lernen?
Dieser Kurs beschäftigt sich mit der Ableitung von Funktionen.
Genauer gesagt, soll die Ableitung stückweise eingeführt und ihre Eigenschaften mit Übungsaufgaben ausführlich untersucht werden.

2 Lernziele
Am Ende dieses Kurses...
... kennst du die Begriffe "mittlere Änderungsrate" und "momentane (lokale) Änderungsrate" und deren Unterschied zueinander.
... kannst du mittlere Änderungsraten berechnen und momentane Änderungsraten annähern.
... kannst du das Bilden der Ableitung aus einem Grenzwertprozess in eigenen Worten beschreiben.

3 Wo stehen wir gerade?
Wir untersuchen Funktionen, die eine große Vielfalt von Eigenschaften besitzen: Achsenschnittpunkte, Symmetrie usw. und heute lernen wir eine weitere, sehr wichtige Eigenschaft kennen.
Hierzu eine Situation, die du sicherlich schon aus deinem Alltag kennst:
Ein Auto beschleunigt aus dem Stand los und legt immer schneller werdend eine Strecke zurück.
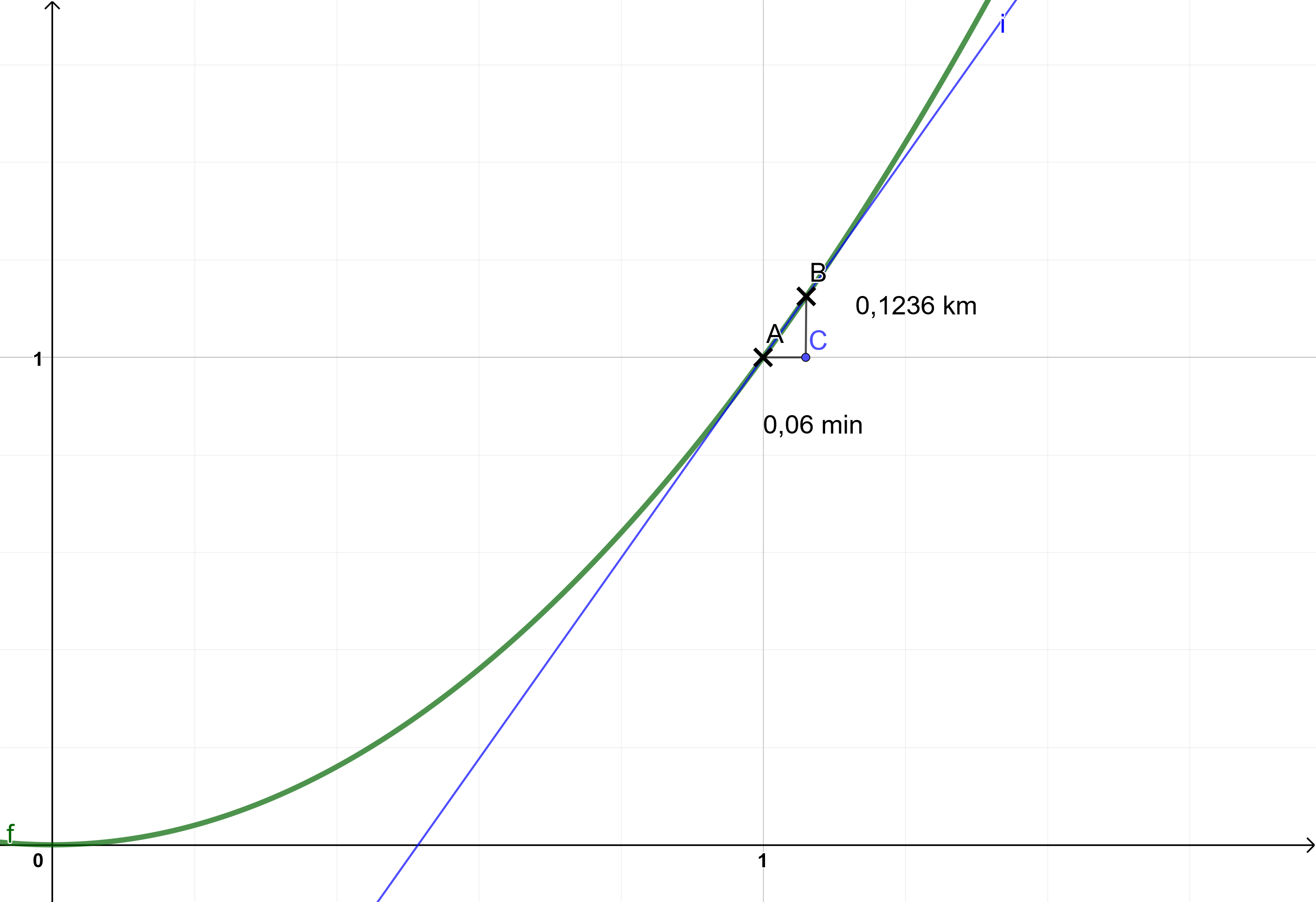
Der Graph rechts zeigt eine Funktion, die angibt, wie viele Kilometer (auf der y-Achse) das Auto nach Minuten (auf der x-Achse) zurücklegt.
Der Funktionsterm lautet
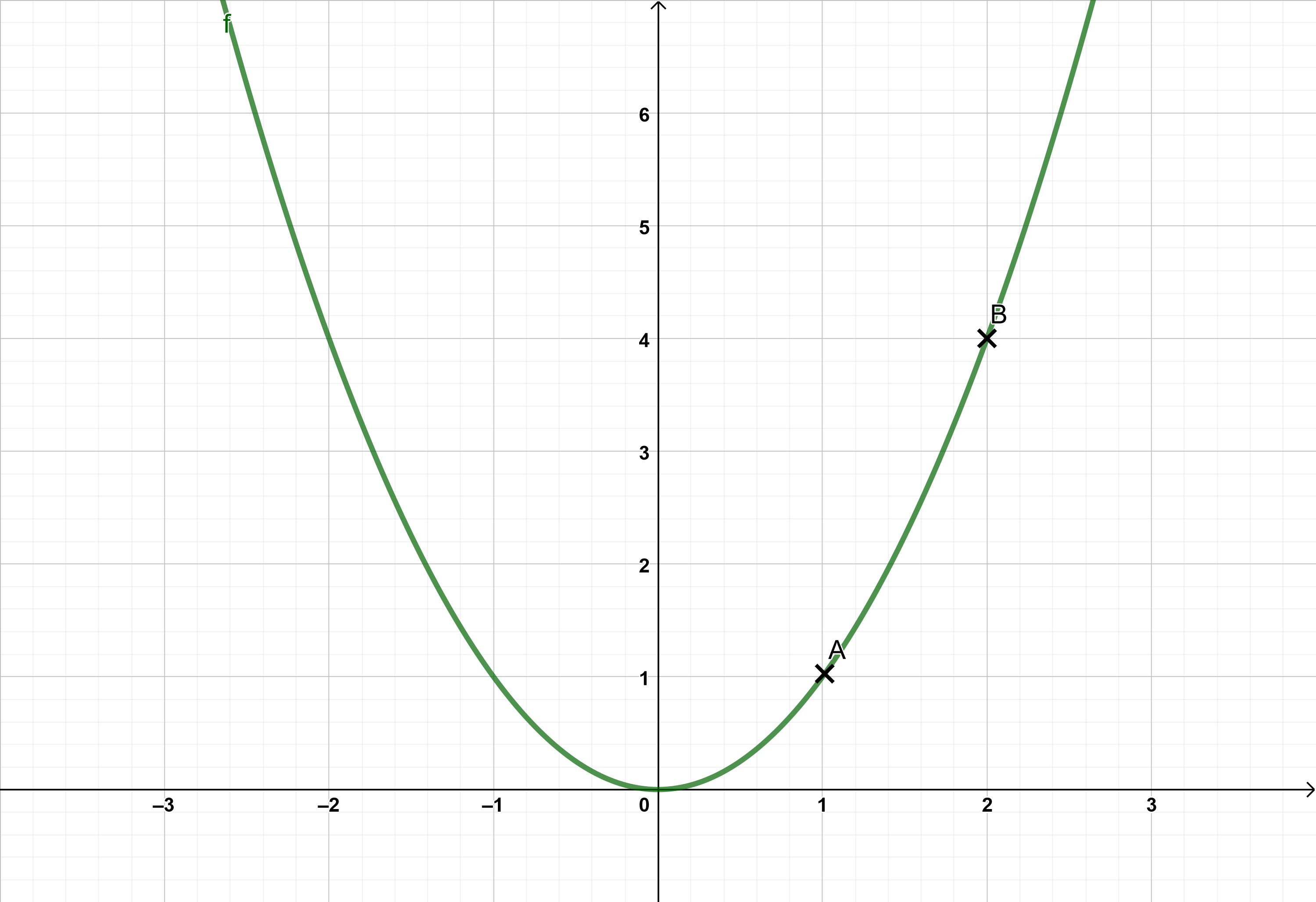
Man kann anhand des Graphen ablesen, dass am Punkt A gilt: (Das Auto hat nach einer Minute einen Kilometer zurückgelegt.) oder auch am Punkt B gilt: (Nach zwei Minuten wurden 4 Kilometer gefahren.). Aber: Wie schnell fährt das Auto eigentlich?
4 Die mittlere Änderungsrate
Die Geschwindigkeit lesen wir in unserem Auto am Tacho ab. Jetzt ist das ein bisschen anders, doch mit einer kleinen Überlegung können wir mit unserer Funktion herausfinden, wie schnell wir sind.
Eine Geschwindigkeit, beispielsweise gibt an, dass man pro Stunde zurücklegt. Also eine bestimmte Strecke, die in einer festgelegten Zeit gefahren wird, führt auf eine Geschwindigkeit.
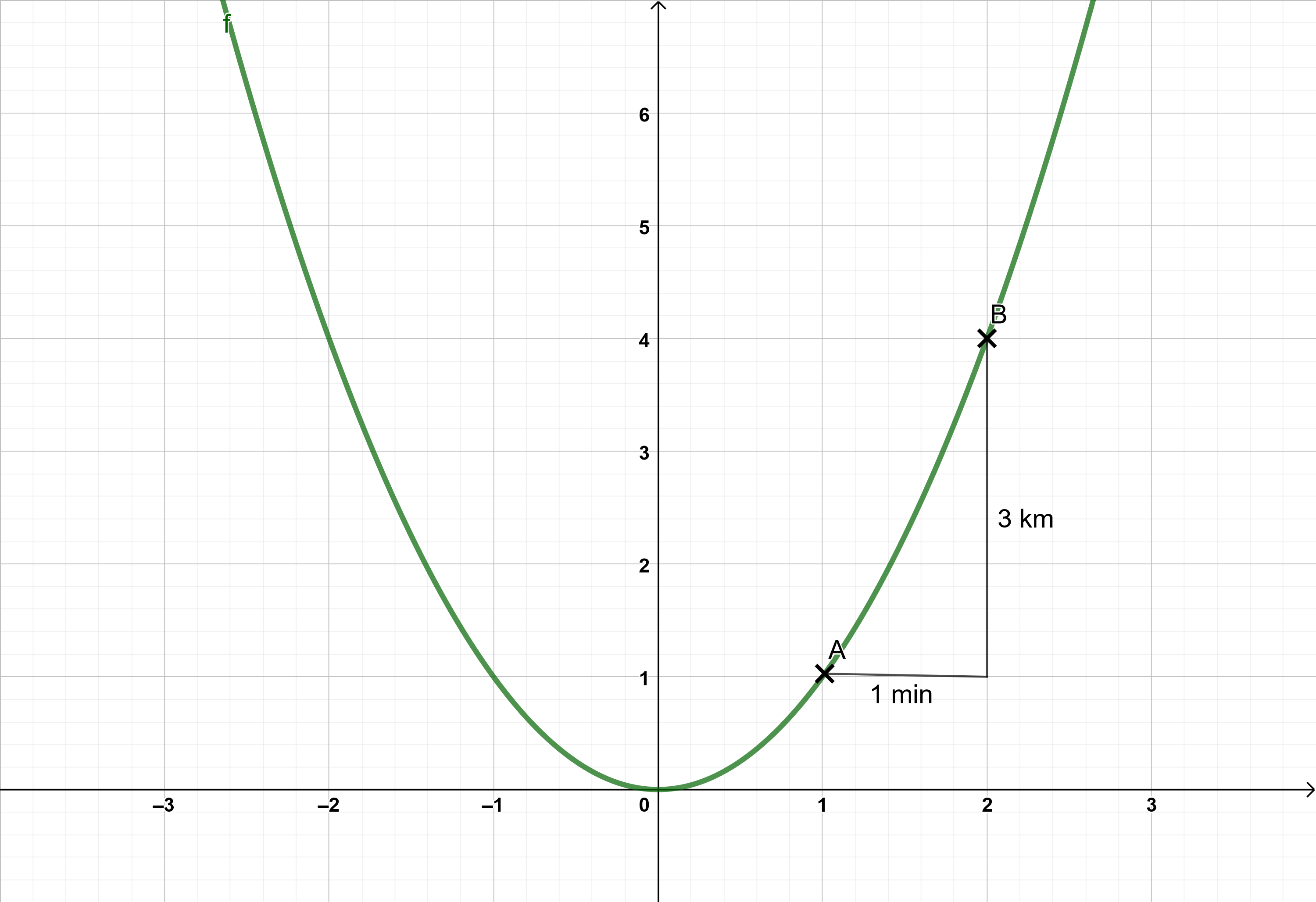
Möchte ich also wissen, wie schnell ich durchschnittlich von Punkt A nach Punkt B gefahren bin, lese ich ab, dass in in einer Minute gefahren bin und erhalte
als meine Geschwindigkeit.
5 Die mittlere Änderungsrate
Hier wurde ein bisschen geschummelt. Denn eigentlich wissen wir, dass das Auto beschleunigt und dabei immer schneller wird. Die Geschwindigkeit müsste in jedem Moment eigentlich größer werden, wie kann sie dann eine Minute lang gleich sein?
Wir haben uns gerade der Einfachheit halber vorgestellt, wir würden zwischen A und B gleich schnell fahren.
Damit haben wir uns eine Art Durchschnittslinie in unseren Graphen gebastelt, um an der Linie ein Steigungsdreieck anzulegen.
Diese Gerade, die durch A und B verläuft, heißt Sekante.
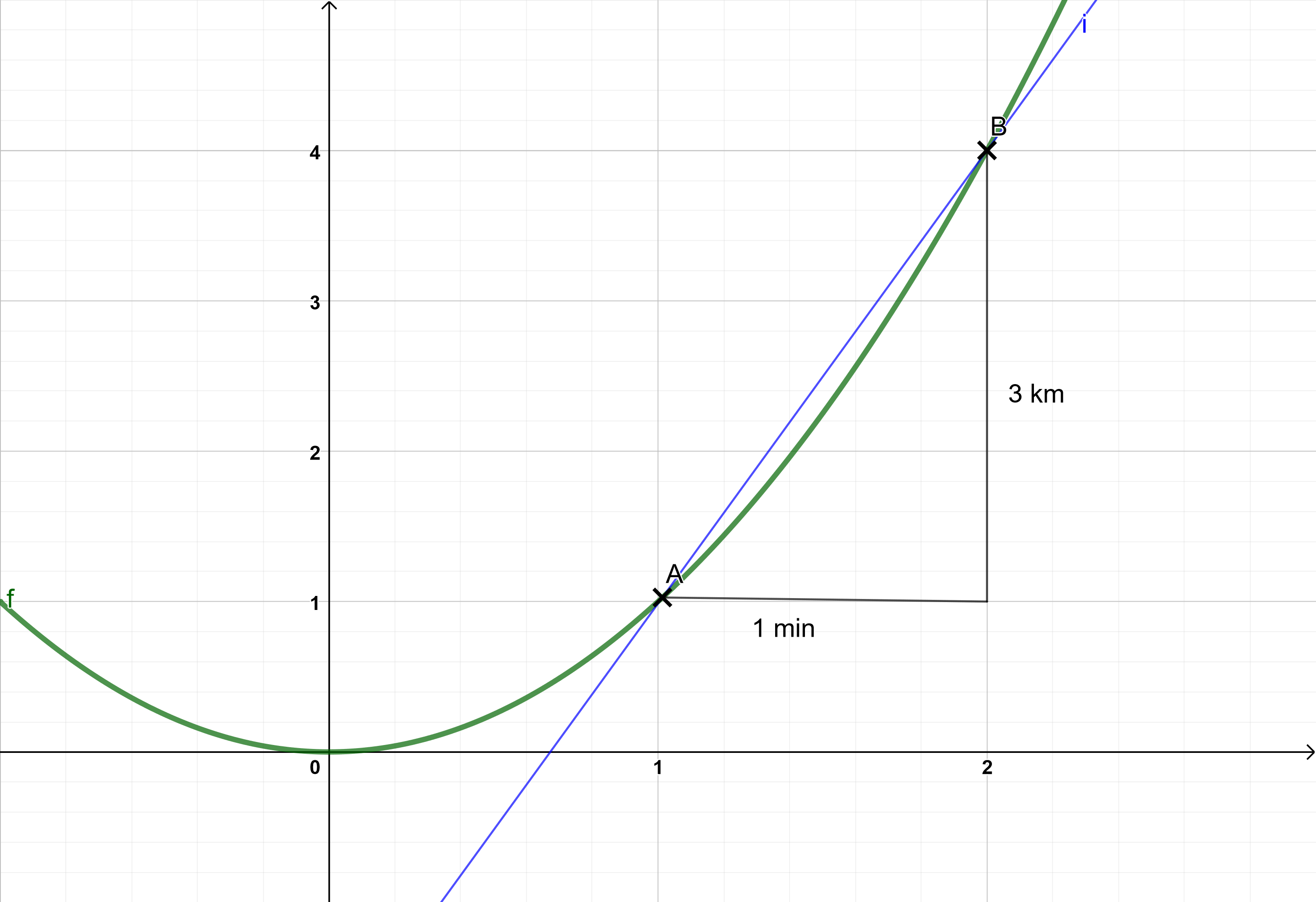
6 Die mittlere Änderungsrate - Sekante
Eine Sekante ist eine Gerade, die durch zwei Punkte einer Funktion schneidend verläuft. Im Applet unten kannst du die Punkte und entlang des blauen Graphen bewegen, um die rote Sekante zu verschieben.
Das gestrichelte Steigungsdreieck zeigt die zurückgelegte Strecke innerhalb einer festgelegten Zeit auf der x-Achse. Rechts daneben wird die mittlere Änderungsrate, also die Durchschnittsgeschwindigkeit über das Verhältnis "Strecke pro Zeit" berechnet.
Probiere dich aus!
7 Die mittlere Änderungsrate - Sekante
Übungsaufgabe
Welche Durchschnittsgeschwindigkeit liegt zwischen und vor?
Beobachte den Wert für , während du von beginnend immer weiter in Richtung bewegst.
Warum wird kein Ergebnis angezeigt, wenn und aufeinander liegen?
8 Eine Annäherung...
Die letzte Frage erscheint etwas komisch. Wie kann mathematisch kein klares Ergebnis herauskommen, wenn es doch eigentlich eine Geschwindigkeit gibt in jedem Moment? Der Tacho im Auto zeigt nämlich keine "Durchschnittsgeschwindigkeiten", sondern eigentlich momentane Geschwindigkeiten.
Versuchen wir doch einmal, die Momentangeschwindigkeit zur Zeit anzunähern.
Rücken wir den Punkt B doch einmal ganz nahe an A heran.
Die mittlere Änderungsrate würde hier
ergeben.
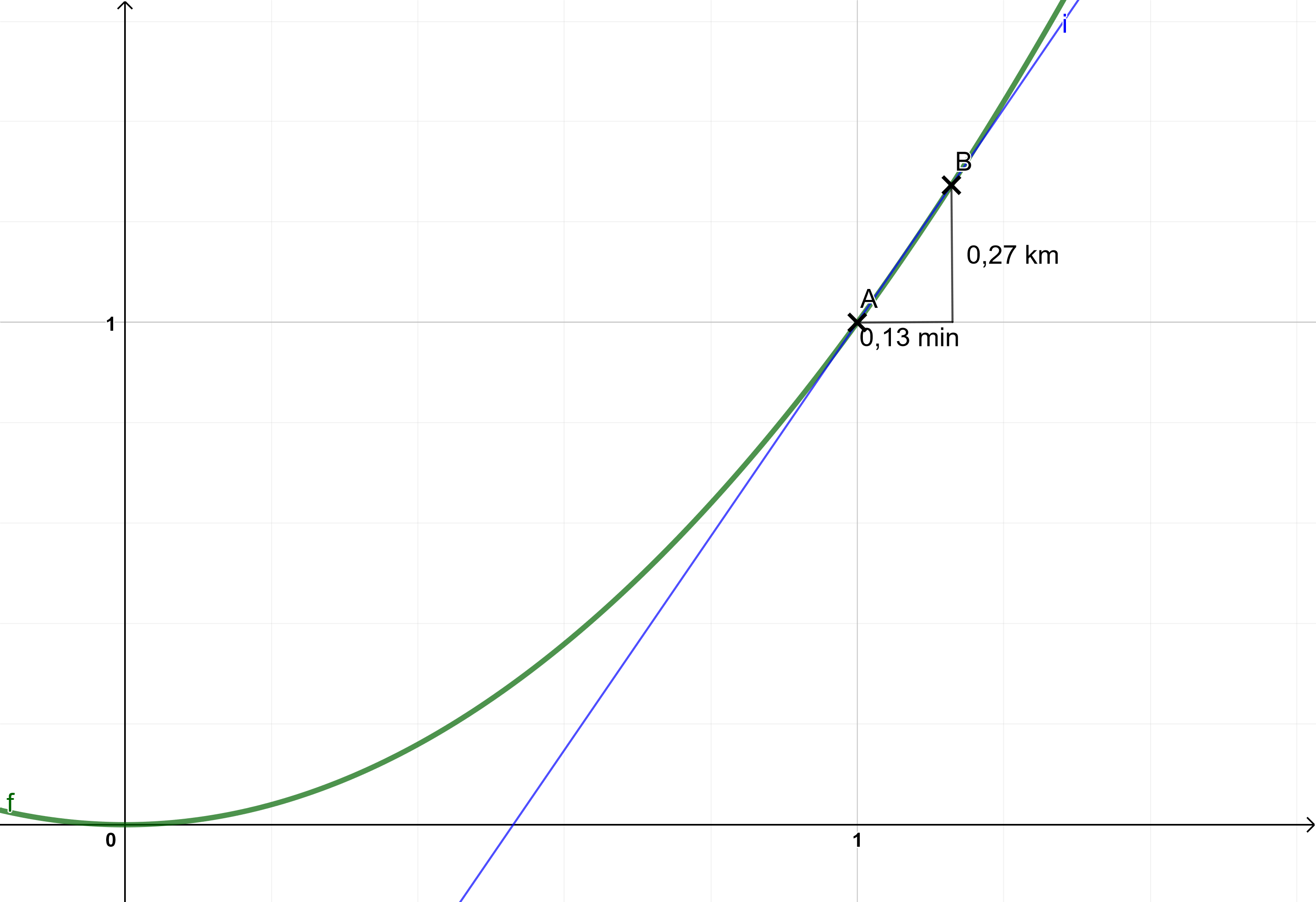
Wir wiederholen das für einen noch näheren Punkt B:
Die mittlere Änderungsrate auf dem noch kleineren Bereich zeigt viel besser, was einer Momentangeschwindigkeit entsprechen würde:
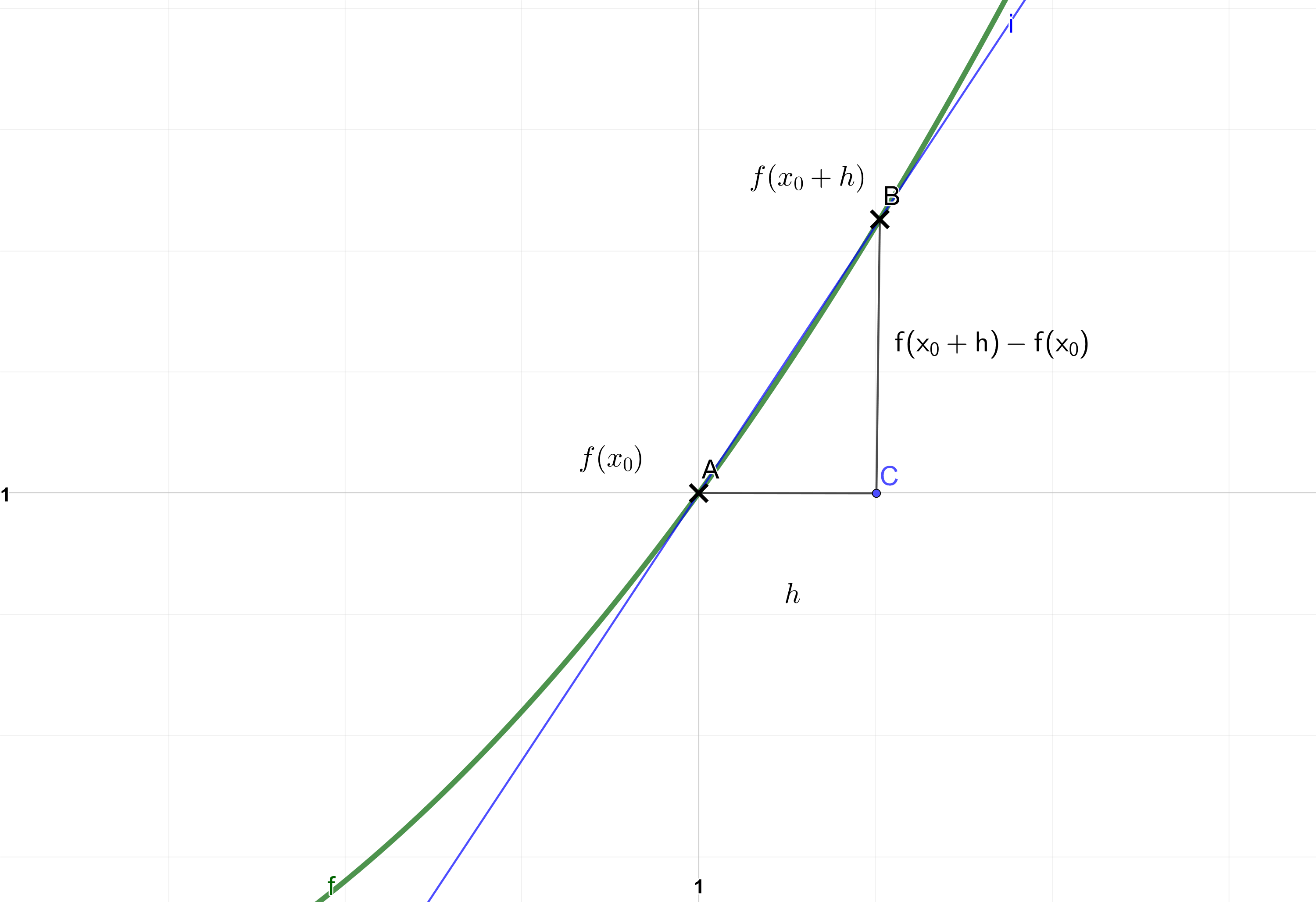
Geometrisch ist die Sekante durch zwei Punkte auf dem Funktionsgraph festgelegt. Nähern wir den einen Punkt nun beliebig nahe zum anderen hin, erhalten wir eine Gerade, die den Funktionsgraphen nur in einem Punkt berührt - eine Tangente.
Also nähern wir eine momentane Änderungsrate von einer mittleren Änderungsrate her.
Übungsaufgabe
Mithilfe der Formel für die mittlere Änderungsrate kann von der Funktion nun eine Momentangeschwindigkeit für "nahe" angenähert werden.
Bestimme den Wert für bei .
Wiederhole diese Berechnung für .
Äußere eine Vermutung, welchem Wert sich dieser Prozess annähert.
9 Die momentane Änderungsrate - Ganz mathematisch!
Trotz dass es so scheint, als würden beide Zahlen fast sein, stellt sich ein Wert von rund ein. Die Annäherung von Punkt B an Punkt A, ist, was man mathematisch ein Grenzwertprozess nennt.
Die mittlere Änderungsrate auf einem sehr sehr kleinen Bereich, der nur breit ist, lässt sich berechnen durch:
bezeichnet den Funktionswert an der Stelle , in dem wir uns die momentane Änderungsrate anschauen möchten.
ist der Funktionswert an der Stelle, die weiter rechts liegt. Die Differenz der beiden Funktionswerte ist wichtig für das Verhältnis, wie oben formuliert.
Da man für die tatsächliche momentane Änderungsrate in Punkt A, Punkt B komplett zu A laufen lassen müsste, muss dieser Abstand verschwindend klein werden. Mathematisch wird das formuliert durch den "limes" oder auch anders: "Grenzwert":
Um damit formal eine Ableitung zu berechnen, verwende die h-Methode.
10 Änderungsraten und Ableitung - Eine Übersicht
Mittlere Änderungsrate | Momentane Änderungsrate | |
|---|---|---|
Bedeutung | Gibt einen durchschnittlichen Wert für die Steigung auf einem festen Bereich (Intervall) an. | Gibt den Wert einer Steigung genau an einer Stelle an. |
Formel |
Die momentane Änderungsrate an einer Stelle wird auch bezeichnet mit:
Hier wird auch bezeichnet als Ableitung der Funktion in der Stelle .
Die Ableitung ist eine neue Funktion, die an der jeder Stelle als Funktionswerte die Steigung von besitzt.
11 Ausblick
Die Steigung ist eine interessante Eigenschaft, die zum Objekt der Ableitung führt. Diese Ableitung muss nicht jedes Mal formal mit einem Grenzwert berechnet werden, sondern kann mit Ableitungsregeln bestimmt werden.
12 Ende
Danke fürs Mitmachen!
Hinterlasse doch gerne dein Feedback zu diesem Inhalt!
