Teil 2, Analysis 1 - lernen mit Serlo!

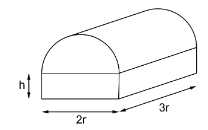
Ein Tiergarten plant den Bau eines Tropenhauses, in dem ein künstliches Ökosystem mit Lebensbedingungen für tropische Pflanzen-und Tierarten geschaffen werden soll. Das Tropenhaus soll die Form eines Quaders mit aufgesetztem Halbzylinder bekommen. Der Radius des Halbzylinders wird mit $r$ bezeichnet.

Der Quader hat die Breite $2 r$ , die Länge $3 r$ und die Höhe $h$ (siehe Skizze).

Um möglichst ideale klimatische Bedingungen zu schaffen, sollen die Außenwände des Tropenhauses und das Dach aus Glas bestehen. Hierfür sind $1000 m^{2}$ Glas vorgesehen.

Die Maßzahl des Volumens des Tropenhauses in Abhängigkeit vom Radius $r$ des Halb-zylinders lässt sich durch die Funktionswerte der Funktion $V : r \mapsto V (r)$ beschreiben.

Aus den Baurichtlinien geht hervor, dass der Radius $r$ des Halbzylinders maximal $8,5 m$ betragen darf. Der Tiergartenbetreiber fordert hierfür mindestens $4 m$ .

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

Tropenhaus aus Abiturprüfung FOS Bayern 2022 Analysis I Teil 2 Aufgabe 3

Stellen Sie eine Gleichung der Funktion $V$ auf. Bestimmen Sie dazu vorab die Maßzahl $A$ des Flächeninhalts der insgesamt zu verglasenden Oberfläche des Tropenhauses in Abhängigkeit des Radius des Halbzylinders und der Höhe des Quaders. (6 BE)

(Mögliche Ergebnisse: $A (r, h) = 10 r h + 4 π r^{2}$ und $V (r) = 600 r - 0,9 π r^{3}$ )

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

Volumen von Quader und Halbzylinder

Der Quader, der den unteren Teil des Tropenhauses bildet, hat das Volumen

Allgemeiner Term
	↓
$V_{Q}$	$=$	$l \cdot b \cdot h$
	↓	Anpassung auf die Situation (Angaben aus Text und Skizze).
$V_{Q}$	$=$	$2 r \cdot 3 r \cdot h$
	↓	Vereinfache.
$V_{Q}$	$=$	$6 r^{2} h$

Der halbe Zylinder, der das Dach des Tropenhauses bildet, hat das Volumen

Allgemeiner Term: Hälfte vom Zylindervolumen
	↓
$V_{H Z}$	$=$	$\frac{1}{2} \cdot V_{Z}$
$V_{H Z}$	$=$	$\frac{1}{2} \cdot r^{2} π \cdot h$
	↓	Anpassung auf die Situation (Angaben aus Text und Skizze).
$V_{H Z}$	$=$	$\frac{1}{2} \cdot r^{2} π \cdot 3 r$
$V_{H Z}$	$=$	$1,5 r^{3} π$

Hauptbedingung durch Zusammensetzen der Teilkörper

Durch Addition der Volumina ergibt sich das Gesamtvolumen des Tropenhauses. Da dieses maximal sein soll, bildet es die Hauptbedingung oder Zielfunktion des Extremwertproblems:

$V_{G e s a m t}$	$=$	$V_{Q} + V_{H Z}$
	$=$	$6 r^{2} h + 1,5 r^{3} π$

Um das Volumen nur in Abhängigkeit vom Radius auszudrücken, wie es in der Aufgabe verlangt ist, bedarf es noch einer Nebenbedingung, um $h$ zu eliminieren.

Oberflächeninhalt des Tropenhauses

Aus der Angabe geht hervor, dass $1000 m^{2}$ Glas für alle Außenwände verwendet werden sollen (über die Sinnhaftigkeit, dass diese Angabe bereits fix ist, obwohl Radius und Höhe noch nicht feststehen, lässt sich streiten).

Für den Oberflächeninhalt gilt:

$A_{T r o p e n h a u s}$	$=$	$r e c h t e c k i g e S e i t e n w ä n d e d e s Q u a d e r s + 2 \cdot Halbkreis bei Dach + \frac{1}{2} \cdot Mantelfläche des Zylinders, der das Dach bildet.$
	↓	Mit den Formeln von Rechteck, Kreis und Mantelfläche des Zylinders ergibt sich in der Situation:
$A_{T r o p e n h a u s}$	$=$	$2 r \cdot h \cdot 2 + 3 r \cdot h \cdot 2 + 2 \cdot \frac{1}{2} \cdot r^{2} π + \frac{1}{2} \cdot 2 r π \cdot 3 r$
	↓	Vereinfache.
$A_{T r o p e n h a u s}$	$=$	$10 r h + 4 π r^{2}$

(Diese Gleichung ist als Kontrollergebnis angegeben.)

Aufgrund der oben erwähnten Glasmenge, die verbaut werden soll, ergibt sich die Gleichung $1000 = 10 r h + 4 π r^{2}$ als Nebenbedingung.

Angabe der Zielfunktion in Abhängigkeit von r

Forme nun die Nebenbedingung nach $h$ um und setze sie in die Hauptbedingung ein.

$1000$	$=$	$10 r h + 4 π r^{2}$	$- 4 π r^{2}$
$1000 - 4 π r^{2}$	$=$	$10 h r$	$: 10 r$
$\frac{1000 - 4 π r^{2}}{10 r}$	$=$	$h$

Setze $h$ in die Hauptbedingung ein:

$V$	$=$	$6 r^{2} \cdot h + 1,5 r^{3} π$
	↓	Ersetze durch den linken Teil der obigen Gleichung
	$=$	$6 r^{2} \cdot \frac{1000 - 4 π r^{2}}{10 r} + 1,5 r^{3} π$
	↓	Vereinfache.
	$=$	$600 r - 2,4 π r^{3} + 1,5 π r^{3}$
	↓	Fasse zusammen.
	$=$	$600 r - 0,9 π r^{3}$

Als Funktion $V : r \mapsto V (r)$ ergibt sich also:

$V (r) = 600 r - 0,9 π r^{3}$

(Dieser Term ist als Kontrollergebnis gegeben.)

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Um den Pflanzen und Tieren möglichst viel Lebensraum zur Verfügung zu stellen, soll das Tropenhaus maximalen Rauminhalt besitzen.
Bestimmen Sie den Radius $r$ so, dass die Maßzahl des Volumens des Tropenhauses den absolut größten Wert annimmt und geben Sie diesen maximalen Wert an. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen. (7 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Definitionsmenge von V
Aus dem Angabentext kannst du entnehmen, dass der Radius mindestens $4 m$ und maximal $8,5 m$ groß sein soll. Du musst also zur Angabe der Definitionsmenge keine Überlegungen/Berechnungen durchführen und erhältst direkt:
$D = [4; 8,5]$
Beachte, dass es aufgrund der eingeschlossenen Intervallgrenzen Randextrema gibt.
Kandidaten für Extremstellen mithilfe der 1. Ableitung
Bilde die 1. Ableitung $V^{'} (r)$ :
$V^{'} (r) = 600 - 2,7 π r^{2}$
Bestimme die Nullstellen der 1. Ableitung:
$V^{'} (r)$ $=$ $0$
$600 - 2,7 π r^{2}$ $=$ $0$ $+ 2,7 π r^{2}$
$600$ $=$ $2,7 π r^{2}$ $: (2,7 π)$
$70,74$ $\approx$ $r^{2}$
↓
Beim Radizieren (Wurzelziehen) ergeben sich zwei Lösungen.
$r_{1}$ $\approx$ $8,41$
$r_{2}$ $\approx$ $- 8,41$
Da $r_{2} \notin D$ muss diese potentielle Extremstelle nicht weiter untersucht werden.
Art der Extremstelle
Du kannst die Art der Extremstelle zum Beispiel mithilfe der 2. Ableitung bestimmen. Alternativ geht es auch über eine Monotonietabelle.
$V^{''} (r) = - 5,4 π r$
Setze $r_{1} = 8,41$ in $V^{''}$ ein. Du benötigst nur das Vorzeichen der Lösung, nicht den genauen Wert.
$V^{''} (8,41) = - 5,4 π \cdot 8,41 < 0 \Rightarrow$ Hochpunkt/Maximum vom Graphen von $V$
Zugehöriges Volumen
Setze deine gefundene Extremstelle in den Term von $V$ ein, um das zugehörige Volumen in Abhängigkeit vom gefundenen Radius zu berechnen:
$V (8,41) = 600 \cdot 8,41 - 0,9 \cdot π \cdot {(8,41)}^{3} \approx 3364,18$
Randextrema
Da die Ränder des Definitionsbereichs selbst in der Definitionsmenge enthalten sind, musst du überprüfen, ob das Volumen dort größer ist als beim gerade berechneten Maximum (suche nach dem globalen Maximum im Definitionsbereich).
$V (4) \approx 2219,04 < V (8,41)$ und
$V (8,5) \approx 3363,60 < V (8,41)$ und somit absolutes Maximum bei $(8,41 | 3364,18)$ .
Antwort im Sachkontext
Unter Beachtung der vorhandenen Menge an Glasplatten entsteht das größte Volumen $3364,18 m^{3}$ , wenn der Radius $8,41 m$ beträgt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verwende in jedem Fall das angegebene Endergebnis $V (r) = 600 r - 0,9 π r^{3}$ zur weiteren Rechnung.
Bestimme den Definitionsbereich von $r$ aus dem Angabentext. Er ist wichtig für die berechneten Extremstellen und für eventuelle Randextrema.
Bestimme z. B. mithilfe von 1. und 2. Ableitung die Kandidaten für Extremstellen und ihre Art.
Bestimme das zugehörige Volumen beim Hochpunkt.
Untersuche die Volumina an den Rändern des Definitionsbereichs (Randextrema).
Formuliere einen Antwortsatz mit dem absolut größten Volumen.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$V^{'} (r)$	$=$	$0$
$600 - 2,7 π r^{2}$	$=$	$0$	$+ 2,7 π r^{2}$
$600$	$=$	$2,7 π r^{2}$	$: (2,7 π)$
$70,74$	$\approx$	$r^{2}$
	↓	Beim Radizieren (Wurzelziehen) ergeben sich zwei Lösungen.
$r_{1}$	$\approx$	$8,41$
$r_{2}$	$\approx$	$- 8,41$

Volumen von Quader und Halbzylinder

Hauptbedingung durch Zusammensetzen der Teilkörper

Oberflächeninhalt des Tropenhauses

Angabe der Zielfunktion in Abhängigkeit von r

Hast du eine Frage oder Feedback?

Definitionsmenge von V

Kandidaten für Extremstellen mithilfe der 1. Ableitung

Art der Extremstelle

Zugehöriges Volumen

Randextrema

Antwort im Sachkontext

Hast du eine Frage oder Feedback?