Teil 2, Analysis 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellungen zum Ausdrucken findest du hier als PDF.
- 1
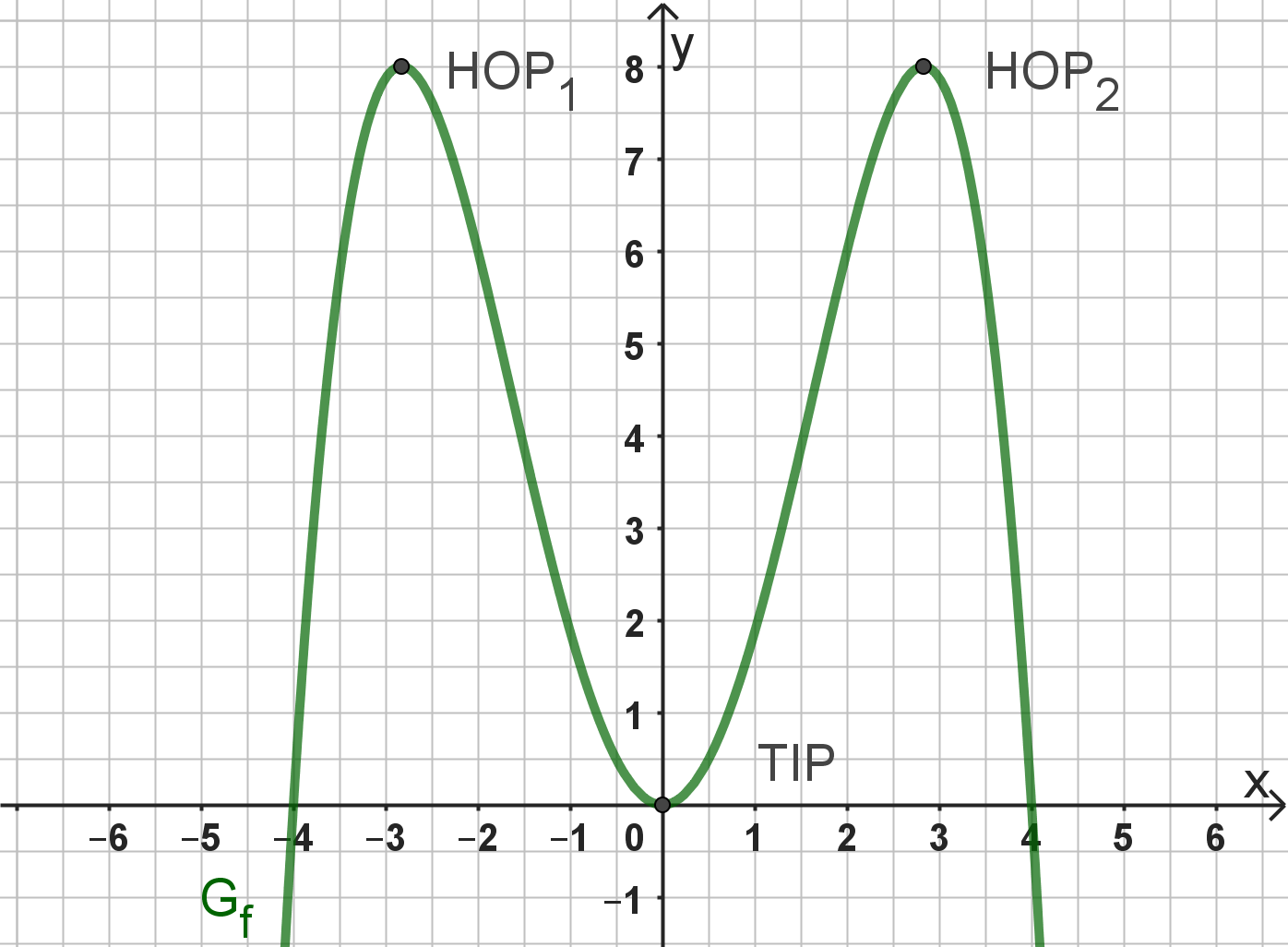
Gegeben ist die Funktion mit der Definitionsmenge . Der Graph der Funktion in einem kartesischen Koordinatensystem wird mit bezeichnet.
Ermitteln Sie die maximalen Monotonieintervalle der Funktion sowie die Art und die Koordinaten der relativen Extrempunkte von . Geben Sie die Wertemenge an. (9 BE)
Berechnen Sie die Wendestelle des Graphen von und entscheiden Sie begründet, ob es sich dabei um Stellen mit maximaler positiver bzw. maximaler negativer Steigung von handelt oder nicht. (6 BE)
Gegeben ist die Funktion mit der Definitionsmenge . Zeigen Sie rechnerisch, dass die Gerade Tangente an den Graphen an der Stelle ist. (2 BE)
Zeichnen Sie unter Verwendung bisheriger Ergebnisse und weiterer geeigneter Funktionswerte den Graphen für in ein kartesisches Koordinatensystem. Maßstab für beide Achsen: . (4 BE)
- 2
Während das Bundesamt für Naturschutz seit Jahren die Ausbreitung von Wölfen in Deutschland fördert, fordern u.a. Weidetierhalter und Jäger zunehmend eine Aufhebung des Abschussverbots von Wölfen. Um über die eventuelle Aufhebung dieses Verbots zu entscheiden, soll die Entwicklung der Anzahl der Wolfsrudel in Deutschland modelliert werden. Die Entwicklung seit dem Jahr lässt sich näherungsweise durch die Funktion mit der Funktionsgleichung mit und darstellen. Der Funktionswert von gibt die Anzahl der Wolfsrudel in Deutschland zum Zeitpunkt an. Dabei steht für die seit Ende des Jahres vergangene Zeit in Jahren. Ende des Jahres wurden Wolfsrudel in Deutschland gezählt, Ende lag die Zahl der Wolfsrudel bereits bei .
Bestimmen Sie die Werte der Parameter und der Funktion . Runden Sie ganzzahlig und auf drei Nachkommastellen.
Im Folgenden gilt
Das Bundesamt für Naturschutz geht davon aus, dass Deutschland maximal Lebensraum für Rudel bieten kann. Berechnen Sie, in welchem Jahr die Anzahl der Wolfsrudel laut dem Modell voraussichtlich diesen Wert erreicht.
Geben Sie die Funktionsgleichung der Funktion in der Form an und folgern Sie daraus die prozentuale Zunahme der Anzahl der Wolfsrudel pro Jahr. Runden Sie auf drei Nachkommastellen.
- 3
Ein Tiergarten plant den Bau eines Tropenhauses, in dem ein künstliches Ökosystem mit Lebensbedingungen für tropische Pflanzen-und Tierarten geschaffen werden soll. Das Tropenhaus soll die Form eines Quaders mit aufgesetztem Halbzylinder bekommen. Der Radius des Halbzylinders wird mit bezeichnet.
Der Quader hat die Breite , die Länge und die Höhe (siehe Skizze).
Um möglichst ideale klimatische Bedingungen zu schaffen, sollen die Außenwände des Tropenhauses und das Dach aus Glas bestehen. Hierfür sind Glas vorgesehen.
Die Maßzahl des Volumens des Tropenhauses in Abhängigkeit vom Radius des Halb-zylinders lässt sich durch die Funktionswerte der Funktion beschreiben.
Aus den Baurichtlinien geht hervor, dass der Radius des Halbzylinders maximal betragen darf. Der Tiergartenbetreiber fordert hierfür mindestens .
Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.
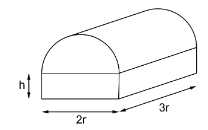
Stellen Sie eine Gleichung der Funktion auf. Bestimmen Sie dazu vorab die Maßzahl des Flächeninhalts der insgesamt zu verglasenden Oberfläche des Tropenhauses in Abhängigkeit des Radius des Halbzylinders und der Höhe des Quaders. (6 BE)
(Mögliche Ergebnisse: und )
Um den Pflanzen und Tieren möglichst viel Lebensraum zur Verfügung zu stellen, soll das Tropenhaus maximalen Rauminhalt besitzen.
Bestimmen Sie den Radius so, dass die Maßzahl des Volumens des Tropenhauses den absolut größten Wert annimmt und geben Sie diesen maximalen Wert an. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen. (7 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?