1 Übersicht
In diesem Kurs lernst du, wie du aus einer Vierfeldertafel ein Baumdiagramm aufstellen kannst. Dabei gibt es immer zwei mögliche Baumdiagramme zu einer Vierfeldertafel.
Das brauchst du:
Du weißt, was ein Baumdiagramm ist
Du weißt, was eine Vierfeldertafel ist
Du weißt, was Wahrscheinlichkeiten sind und was die Mengenverknüpfung macht
Du kennst die Pfadregeln
2 Ausgangssituation
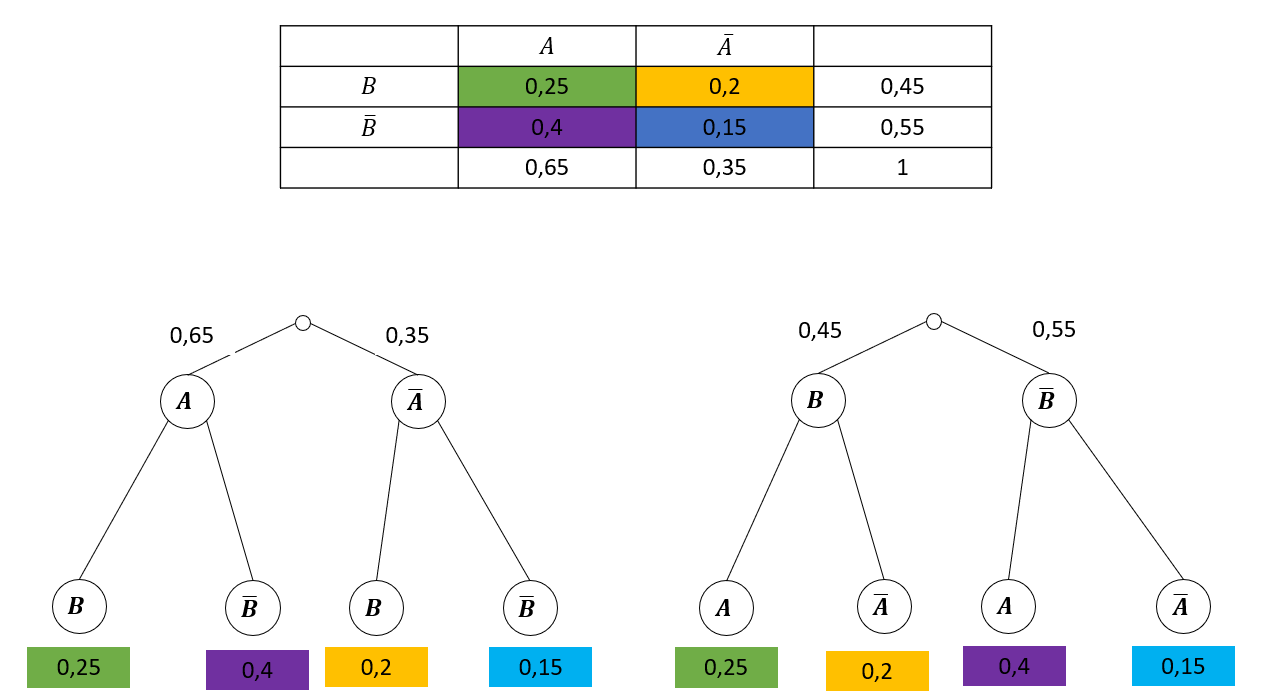
Du hast eine vollständig ausgefüllte Vierfeldertafel vorgegeben und möchtest sie in ein Baumdiagramm umwandeln, zum Beispiel so:
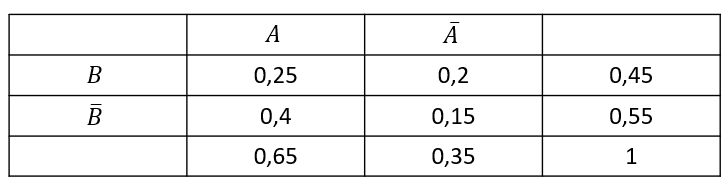
Zur Erinnerung: Außen im Spalten- und Zeilenkopf findest du die Merkmale, hier A und B sowie ihre Gegenereignisse. Alle anderen Felder enthalten Wahrscheinlichkeiten bestimmter Ereignisse.
In der linken, oberen Ecke ist zum Beispiel die Wahrscheinlichkeit, dass A und B beide eintreten/zutreffen. In der untersten Zeile und rechten Spalte findest du neben der Gesamtwahrscheinlichkeit von 100% (=1) auch die Wahrscheinlichkeiten von und .

3 Schritt 1: Baum skizzieren
Es gibt immer zwei mögliche Bäume zu einer Vierfeldertafel. Sie unterscheiden sich darin, welches Merkmal auf der 1. Stufe des Baumes steht. Für die Merkmale A und B sieht das zum Beispiel so aus:
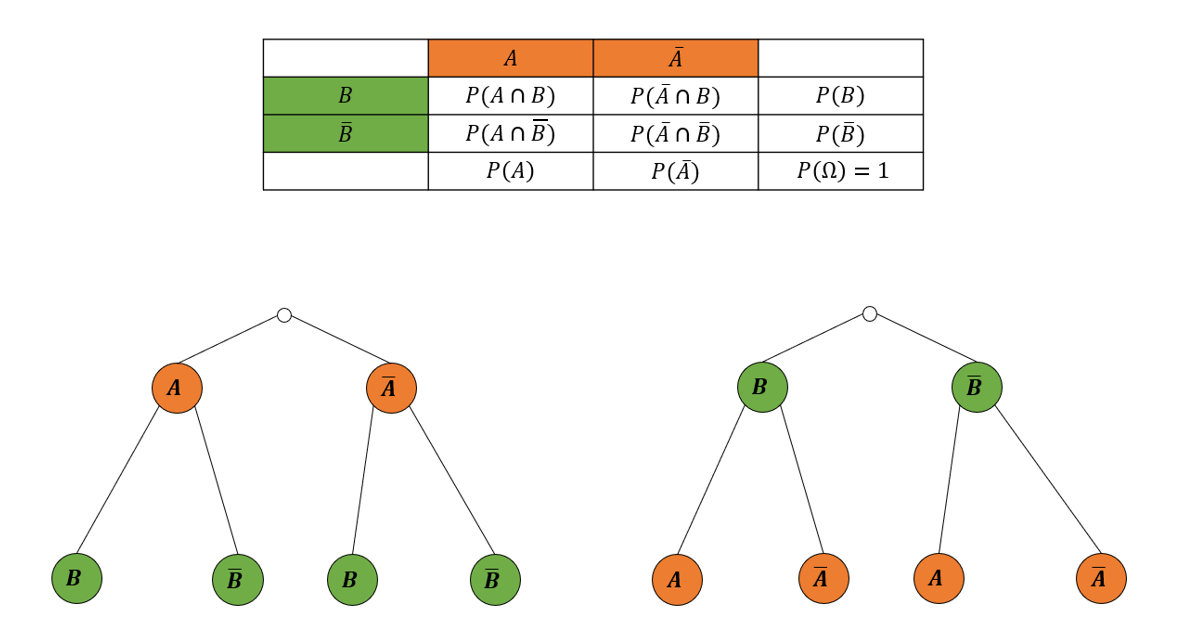
Meistens ist nur ein Baum gefragt. In diesem Kurs wirst du aber beide Beispiele mit verfolgen, um die Unterschiede am Ende vergleichen zu können.
4 Schritt 2: Wahrscheinlichkeiten der Merkmale
In der untersten Zeile und rechten Spalte findest du, wie zuvor schon erwähnt, die Wahrscheinlichkeiten und , also die Wahrscheinlichkeiten der einzelnen Merkmale.
Diese kannst du in die erste Stufe des Baums übertragen.
Die Wahrscheinlichkeiten in der rechten Spalte gehören in unserem Beispiel dabei zum rechten Baum, in dem B auf der ersten Stufe steht.
Die Wahrscheinlichkeiten in der unteren Zeile gehören zum linken Baum, in dem A auf der ersten Stufe steht.
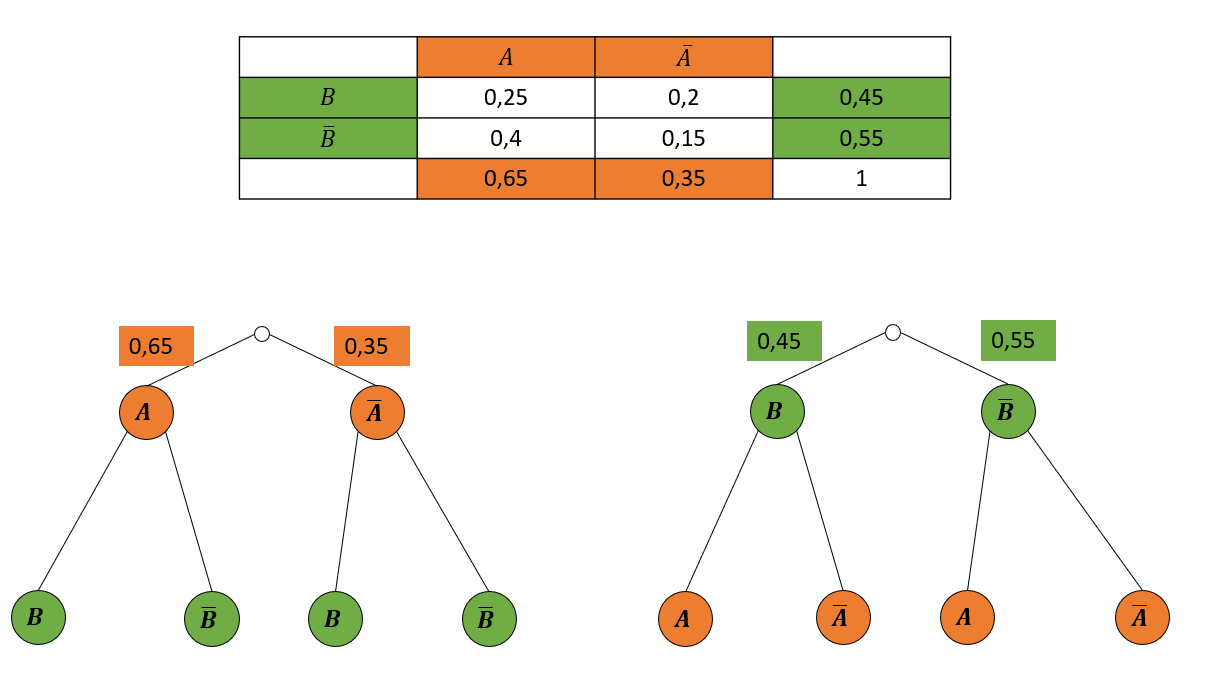
Die Wahrscheinlichkeit auf der 2. Stufe kann nicht aus der Vierfeldertafel übertragen werden. Mehr dazu lernst du später.
5 Schritt 3: Wahrscheinlichkeiten der Pfade
Unter dem Pfad kannst du die Wahrscheinlichkeiten der jeweiligen Schnittmengen angeben. Bei beiden Bäumen ist zum Beispiel ganz links , dann geht es aber mit unterschiedlichen Ereignissen weiter.
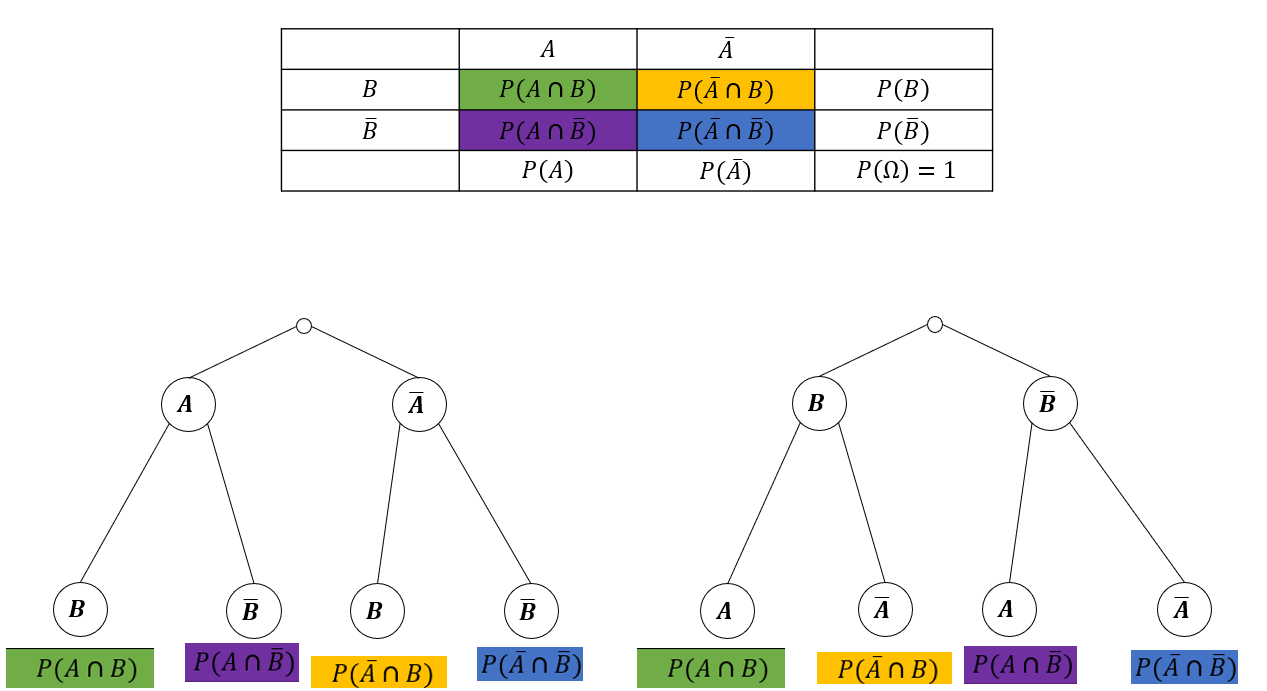
Im Beispiel sieht das dann so aus:
6 Schritt 4: Pfadregeln anwenden
Um die Wahrscheinlichkeiten auf der 2. Stufe zu ermitteln, muss die 1. Pfadregel rückwärts angewendet werden. Die Wahrscheinlichkeit am Ende des Pfades wird durch die Wahrscheinlichkeit auf der 1. Stufe geteilt.
Zum Beispiel:
Für die andere Wahrscheinlichkeit kann dann auch verwendet werden, dass die Summe aller Pfadwahrscheinlichkeiten für alle Pfade, die von einem Knoten ausgehen, 1 sein muss.
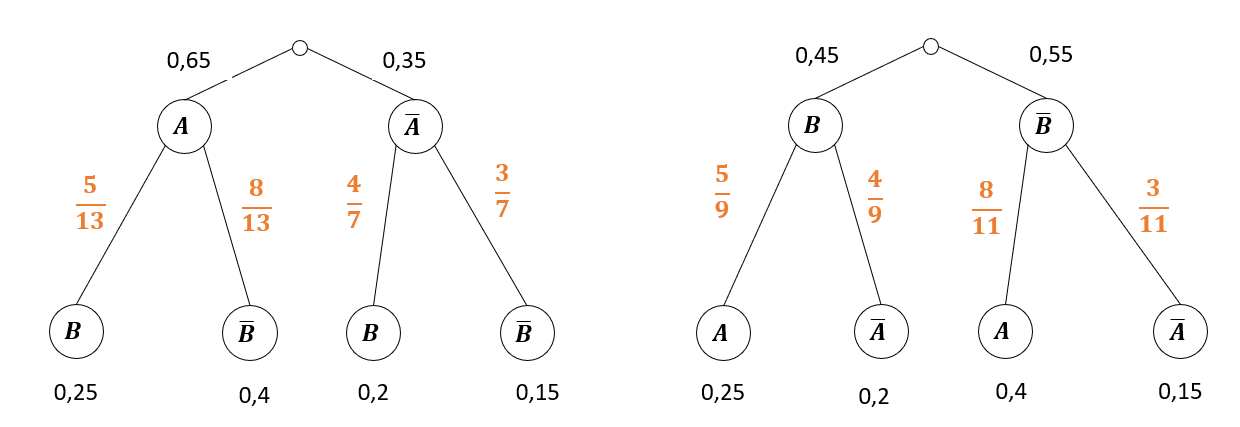
Beide Bäume sind für unterschiedliche Fragestellungen relevant.
Die Frage "Mit welcher Wahrscheinlichkeit tritt B ein, wenn zuvor A nicht eingetreten ist?" lässt sich mit dem linken Baum (leichter) beantworten. Hier ist A auf der ersten Stufe des Baums.
Die Frage "Mit welcher Wahrscheinlichkeit tritt A nicht ein, wenn B zuvor schon eingetreten ist?" lässt sich mit dem rechten Baum (leichter) beantworten. Hier ist nämlich B auf der ersten Stufe.
7 Jetzt bist du dran!
Laden
