Teil 2, Stochastik 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellungen zum Ausdrucken findest du hier
- 1
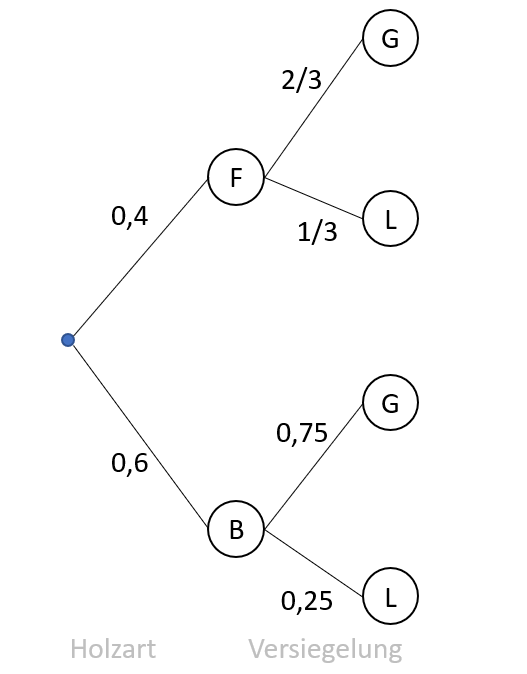
Ein Schreiner hat sich auf die Herstellung maßangefertigter Möbel spezialisiert. Er fertigt seine Möbel aus Fichten- oder Buchenholz und bietet sie mit gewachster (G) oder lackierter (L) Oberfläche an.
Erfahrungsgemäß entscheiden sich 40% seiner Kunden für Möbel aus Fichtenholz (F). Jeder dritte Kunde, der Möbel aus Fichtenholz in Auftrag gibt, bestellt diese mit lackierter Oberfläche. Unter den Kunden, die sich für die Holzart Buche (B) entscheiden, beträgt der Anteil derer, die ihre Möbel mit gewachster Oberfläche bestellen, 75%.
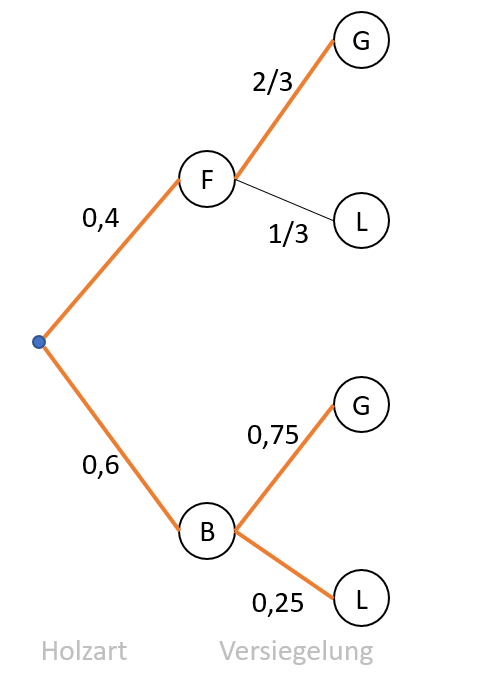
Berechnen Sie unter Verwendung eines Baumdiagramms den prozentualen Anteil von gewachsten Möbeln am Verkauf.
Berechnen Sie
- 2
Für eine Zufallsgröße X ist die zugehörige Wahrscheinlichkeitsverteilung mit durch folgende Tabelle vollständig gegeben:
x
1
2
3
4
5
6
P(X=x)
a
b-a
0,2
b
0,08
0,02
Bestimmen Sie die Werte für die Parameter a und b, wenn gilt. (Teilergebnis: )
Die Lieferzeiten für die Möbel des Schreiners aus 1.0 sind abhängig von verschiedenen Faktoren, wie z.B. Auftragslage und Bestellumfang. Der Schreiner hat sich über die Jahre hinweg die Lieferzeiten ab Auftragseingang notiert, um möglichst genaue Angaben zu den Lieferzeiten machen zu können.
Die unter 2.0 aufgeführte Wahrscheinlichkeitsverteilung mit den unter 2.1 (letzte Teilaufgabe) bestimmten Werten für a und b beschreibt die Lieferzeit für die Möbel innerhalb der letzten Jahre. Die Zufallsgröße X gibt die Lieferzeit ab Bestelldatum in vollen Wochen an. Lieferzeiten von mehr als sechs Wochen kamen bisher nicht vor.
Interpretieren Sie den Erwartungswert von X im Sachzusammenhang und ermitteln Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
: "Die Lieferzeit beträgt höchstens vier Wochen."
: "Bei genau drei von neun Bestellungen erfolgt die Lieferung der Möbel innerhalb einer Woche."
: "Bei zehn nacheinander eingegangen Bestellungen erfolgt nur bei der letzten die Lieferung der Möbel erst in der sechsten Woche, alle anderen erfolgen früher.
- 3
Gegen eine Gebühr liefert der Schreiner die gekauften Möbel an seine Kunden aus. Von insgesamt 200 Kunden stammen 80 aus einem Umkreis von 50 km (U) um den Standort der Schreinerei. 128 Kunden nehmen den Lieferservice nicht in Anspruch ().
Um die Auslieferungen besser planen zu können, hat der Schreiner in der folgenden Tabelle die Anzahl der zu beliefernden Kunden (L) - also insgesamt 72 - je nach Bestellumfang und Lieferort dargestellt.
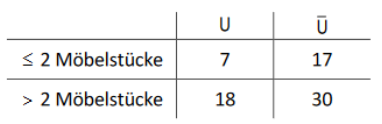
Ergänzen Sie die folgende Vierfeldertafel mithilfe der obigen Angaben.
Bestimmen Sie außerdem die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Kunde mehr als 50 km von der Schreinerei entfernt wohnt und seine Möbel selbst abholt.
200
Beschreiben Sie mit eigenen Worten jeweils die Bedeutung der bedingten Wahrscheinlichkeiten bzw im Sachzusammenhang (ohne sie zu berechnen) und interpretieren Sie die hier geltende Beziehung im Sinne der vorliegenden Thematik.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?