Nachtermin Teil B - lernen mit Serlo!

Aufgabe B4

Der Punkt $A (0 | - 4)$ legt mit den Pfeilen $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ und $\vec{A D_{n}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ für

$φ \in [0^{\circ}; 90^{\circ}]$ Parallelogramme $A B C_{n} D_{n}$ fest.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Berechnen Sie die Koordinaten der Pfeile $\vec{A D_{1}}$ für $φ = 30^{\circ}$ und $\vec{A D_{2}}$ für $φ = 60^{\circ}$ .
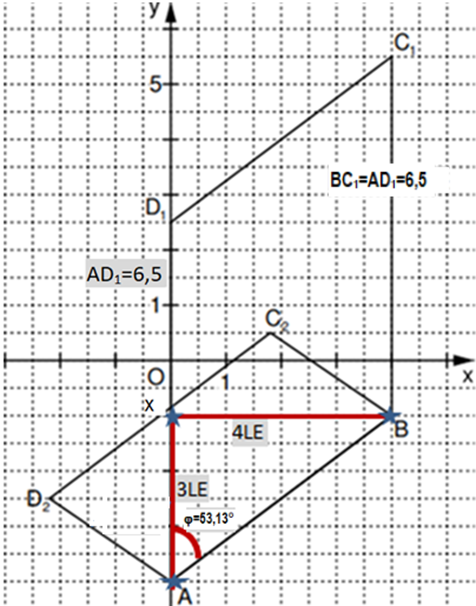
Zeichnen Sie sodann die Parallelogramme $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$ in ein Koordinatensystem ein. (4 P)
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 3 \leq x \leq 5; - 4 \leq y \leq 6$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorrechnung
geg.: $A (0 | - 4)$ , Vektor $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ ; $\vec{A D_{n}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ für $φ \in [0 °; 90 °]$
ges.: Parallelogramme $A B C_{n} D_{n}$ : $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$
Ansatz und Rechnung:
Benutze dabei $\sin 30^{\circ} = \frac{1}{2} = 0,5$ und $\sin 60^{\circ} = \sqrt{\frac{3}{4}} \approx 0,87$
1. Berechnung $\vec{A D_{1}} (für φ = 30 °)$ und $\vec{A D_{2}} (für φ = 60 °)$ :
$\vec{A D_{1}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin 30 ° \\ 9 - 10 \cdot \sin^{2} 30 ° \end{array}) = (\begin{array}{c} 3 - 6 \cdot 0,5 \\ 9 - 10 \cdot {0,5}^{2} \end{array}) = (\begin{array}{c} 3 - 3 \\ 9 - 10 \cdot 0,25 \end{array}) = (\begin{array}{c} 0 \\ 9 - 2,5 \end{array}) = (\begin{array}{c} 0 \\ 6,5 \end{array})$
$\vec{A D_{2}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin 60 ° \\ 9 - 10 \cdot \sin^{2} 60 ° \end{array}) = (\begin{array}{c} 3 - 6 \cdot 0,87 \\ 9 - 10 \cdot {0,87}^{2} \end{array}) = (\begin{array}{c} 3 - 5,2 \\ 9 - 10 \cdot 0,75 \end{array}) = (\begin{array}{c} - 2,2 \\ 9 - 7,5 \end{array}) = (\begin{array}{c} - 2,2 \\ 1,5 \end{array})$
2. Zeichnung: $L E = 1 c m$ ; mit $x : - 3 ≦ x ≦ 5$ und $y : - 4 ≦ y ≦ 6$ ,
mit $A (0 | - 4)$ , $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ , $\vec{A D_{1}} = (\begin{array}{c} 0 \\ 6,5 \end{array})$ und $\vec{A D_{2}} = (\begin{array}{c} - 2,2 \\ 1,5 \end{array})$ Parallelogramme $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$ zeichnen:
Parallelogramme $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnung der Vektoren $\vec{A D_{1}} (für φ = 30 °)$ und
Berechnen Sie das Maß des Winkels $B A D_{1}$ . (1,5 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie, Tangens
geg.: Strecke $X A = 3 L E$ , $X B = 4 L E$
ges.: $∢ B A D_{1}$ , siehe Zeichnung Aufgabe 4a
Ansatz und Rechnung:
$∢ B A D_{1} ≙ ∢ B A X = \tan \frac{𝐆 𝐊}{𝐀 𝐊} = \frac{4}{3} = 1, 3$
$\Rightarrow ∢ 𝐁 𝐀 𝐃_{𝟏} = 𝟓𝟑,𝟏𝟑 °$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Winkel $B A D_{1}$ ist derselbe wie der Winkel $B A X$ mit $X (0 | - 1)$ .
Berechne den Tangens dieses Winkels.
Zeigen Sie rechnerisch, dass für die Koordinaten der Punkte $C_{n}$ in Abhängigkeit
von $φ$ gilt: $C_{n} (7 - 6 \cdot \sin φ | 8 - 10 \cdot \sin^{2} φ)$ . (1,5 P)

geg.: $A (0 | - 4)$ , $O (0 | 0)$ $\Rightarrow$ $\vec{O A} = (\begin{array}{c} 0 - 0 \\ - 4 - 0 \end{array}) = (\begin{array}{c} 0 \\ - 4 \end{array})$ ; $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ ;
$\vec{A D_{n}} = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ $= \vec{B C_{n}}$
ges.: Koordinaten der Punkte $C_{n} (φ)$
Ansatz und Rechnung:
Berechnung mithilfe Vektoraddition $\vec{O C_{n}} = \vec{O A} \oplus︎ \vec{A B} \oplus︎ \vec{B C_{n}}$ mit $φ \in [0 °; 90 °]$
$\Rightarrow \vec{O C_{n}} (φ) = (\begin{array}{c} 0 \\ - 4 \end{array}) \oplus︎ (\begin{array}{c} 4 \\ 3 \end{array}) \oplus︎ (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ mit $φ \in [0 °; 90 °]$
$\Rightarrow \vec{𝐎 𝐂_{𝐧}} (𝛗) = (\begin{array}{c} 𝟕 - 𝟔 \cdot \sin 𝛗 \\ 𝟖 - 𝟏𝟎 \cdot \sin^{𝟐} 𝛗 \end{array})$
somit ist $𝐂_{𝐧} (𝟕 - 𝟔 \cdot \sin 𝛗 | 𝟖 - 𝟏𝟎 \cdot \sin^{𝟐} 𝛗)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnung Vektor $\vec{O C_{n}} (φ)$ und damit die Koordinaten von $C_{n} (φ)$
Der Punkt $C_{3}$ des Parallelogramms $A B C_{3} D_{3}$ liegt auf der $x$ -Achse.
Berechnen Sie die $x$ -Koordinate des Punktes $C_{3}$ . (2,5 P)

geg.: $𝐂_{𝐧} (𝟕 - 𝟔 \cdot 𝐬 𝐢 𝐧 𝛗 | 𝟖 - 𝟏𝟎 \cdot 𝐬 𝐢 𝐧^{𝟐} 𝛗)$
ges.: $x$ für $C_{3}$ auf der $x$ -Achse
Ansatz und Rechnung:
wenn $C_{3}$ auf der $x$ -Achse liegt, dann ist die $y$ -Koordinate $= 0$
$\Rightarrow y : 8 - 10 \cdot \sin^{2} φ = 0 mit φ \in [0 °; 90 °]$
$8 = 10 \cdot \sin^{2} φ | : 10$
$\frac{8}{10} = \sin^{2} φ | \sqrt{}$
$\sqrt{0,8} = \sqrt{\sin^{2} φ} \Rightarrow 0,8944 = \sin φ \Rightarrow φ ≙ 63,43 °$
Berechnung der $x$ -Koordinate durch Einsetzen von $\sin φ = 0,8944$ :
$\Rightarrow 𝐱_{𝐂_{𝟑}} = 77 - 6 \cdot 0,8944 = 7 - 5,37 = 𝟏,𝟔𝟑$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Punkte auf der $x$ -Achse haben die y-Koordinate Null. Berechne daraus $\sin φ$ und damit $x$ .
Das Parallelogramm $A B C_{4} D_{4}$ ist ein Rechteck.
Berechnen Sie den zugehörigen Wert für $φ$ . (3,5 P)

geg.: $A (0 | - 4)$ ; $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ ; $\vec{A D_{n}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$
ges.: $φ$ unter der Bedingung, dass $A B C_{4} D_{4}$ Rechteck ist
Ansatz und Rechnung:
Bedingung für $A B C_{4} D_{4}$ ≙ Rechteck $\Rightarrow$ Skalarprodukt $\vec{A B} ⊙ \vec{A D_{n}} = 0$ :
$(\begin{array}{c} 4 \\ 3 \end{array}) ⊙ (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array}) = 0$ mit $φ \in [0 °; 90 °]$
Formel für Berechnung Skalarprodukt: $\vec{a} ⊙ \vec{b} = (\begin{array}{c} a_{x} \\ a_{y} \end{array}) ⊙ (\begin{array}{c} b_{x} \\ b_{y} \end{array}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y}$
$\Rightarrow 𝟒 \cdot (𝟑 - 𝟔 \cdot \sin 𝛗) + 𝟑 \cdot (𝟗 - 𝟏𝟎 \cdot \sin^{𝟐} 𝛗) = 𝟎 |$ ausmultiplizieren
$12 - 24 \cdot \sin φ + 27 - 30 \cdot \sin^{2} φ = 0 |$ zusammenfassen
$39 - 24 \cdot \sin φ - 30 \cdot \sin^{2} φ = 0 |$ :30
$1,3 - 0,8 \cdot \sin φ - \sin^{2} φ = 0 |$ umschreiben in quadratische Gleichung
$- \sin^{𝟐} 𝛗 - 𝟎,𝟖 \cdot \sin 𝛗 + 𝟏,𝟑 = 𝟎$
Lösung mithilfe der a-b-c-Formel:
1. Berechnung der Determinante $D$ mit $a = - 1$ ; $b = - 0,8$ ; $c = 1,3$
$\Rightarrow 𝐃 = 𝐛^{𝟐} - 𝟒 \cdot 𝐚 \cdot 𝐜 = (- 0,8)^{2} - 4 \cdot (- 1) \cdot (1,3) = 0,64 + 5,2 = 5,84$
$\Rightarrow D > 0 \leftrightarrow$ 2 Lösungen
2. $D$ in a-b-c-Formel einsetzen:
$\Rightarrow \sin 𝛗_{𝟏,𝟐} = \frac{- b \pm \sqrt{D}}{2 a} = \frac{- (- 0,8) \pm \sqrt{5,84}}{2 \cdot (- 1)} = \frac{𝟎,𝟖 \pm 𝟐,𝟒𝟏𝟔𝟔}{- 𝟐}$
$\to \sin φ_{1} = \frac{0,8 + 2,4166}{- 2} = \frac{3,2166}{- 2} = - 1,6083$ nicht definiert!
$\to \sin 𝛗_{𝟐} = \frac{𝟎,𝟖 - 𝟐,𝟒𝟏𝟔𝟔}{- 𝟐} = \frac{- 𝟏,𝟔𝟏𝟔𝟔}{- 𝟐} = 𝟎,𝟖𝟎𝟖𝟑$
$\Rightarrow 𝛗_{𝟐} = 𝟓𝟑,𝟗𝟑 ° \to φ \in [0 °; 90 °]$
$\Rightarrow 𝕃 = [𝟓𝟑,𝟗𝟑 °]$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnung Skalarprodukt mit $\vec{A B}$ und $\vec{A D_{n}} (φ)$ ,
Lösung der trigonometrischen Gleichung mit a-b-c-Formel
Begründen Sie, weshalb für die y-Koordinate aller Punkte $C_{n}$ gilt: $y_{C_{n}} \geq - 2$ . (1,5 P)

geg.: $\vec{O C_{n}} (φ) = (\begin{array}{c} 7 - 6 \cdot \sin φ \\ 8 - 10 \cdot \sin^{2} φ \end{array})$
ges.: Nachweis, dass für $y -$ Koordinate aller Punkte $C_{n}$ gilt: $\begin{array}{l} 𝐲_{𝐜_{𝐧}} ≧ - 𝟐 \end{array}$
Ansatz und Rechnung:
$𝐲_{𝐂_{𝐧}} = 𝟖 - 𝟏𝟎 \cdot \underset{⏟}{\sin^{𝟐} 𝛗} ≧ - 𝟐$
$\underset{⏟}{\sin^{2} φ ≦ 1}$
$10 \cdot 1 ≦ 10$
$\Rightarrow 𝐲_{𝐜_{𝐧}} ≧ 𝟖 - 𝟏𝟎 ≧ - 𝟐$ q.e.d.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Benutze, dass $\sin^{2} φ \leq 1$ ist.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Aufgabe B4

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?