🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.

Die freie Lernplattform

Aufgaben zur Konstruktion von Dreiecken

1
Trage die Punkte $A (2 | - 1)$ und $B (6 | - 1)$ in ein Koordinatensystem (1 LE = 1 cm) ein.
a) Gib 3 Möglichkeiten für die Koordinaten des Punktes $C$ an, so dass das Dreieck $A B C$ einen Flächeninhalt von $4 {cm}^{2}$ hat.
b) Gib auch die Koordinaten eines Punktes $D$ an, so dass das Dreieck einen doppelt so großen Flächeninhalt wie das Dreieck $A B C$ hat.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
Teilaufgabe a)
Trage zuerst die Punkte $A (2 | - 1)$ und $B (6 | - 1)$ in Koordinatensystem ein. Verbinde die beiden Punkte, um eine Seite des Dreiecks $A B C$ einzuzeichnen.
Danach sollst du einen Punkt $C$ finden, sodass das Dreieck $A B C$ einen Flächeninhalt von $4 {cm}^{2}$ hat.
Wenn du $[A B]$ als Grundseite wählst und $h$ die Höhe des Dreiecks ist, berechnest du den Flächeninhalt des Dreiecks $A_{Δ}$ über:
$A_{Δ} = \frac{1}{2} \cdot A B \cdot h$
Berechne $h$ , indem du die Werte für $A B$ und $A_{Δ}$ einsetzt und nach $h$ auflöst:
$A_{Δ}$ soll $4 {cm}^{2}$ sein.
Die Seitenlänge $A B$ kannst du aus dem Koordinatensystem ablesen.
$\Rightarrow A B = 4 cm$
$A_{Δ}$ $=$ $\frac{1}{2} \cdot A B \cdot h$
↓
Setze $A B = 2 cm$ und $A_{Δ} = 4 {cm}^{2}$ ein.
$4 {cm}^{2}$ $=$ $\frac{1}{2} \cdot 4 cm \cdot h$
$4 {cm}^{2}$ $=$ $2 cm \cdot h$ $: 2 cm$
$2 cm$ $=$ $h$
Das Dreieck benötigt also eine Höhe von $2 cm$ . Zeichne 3 verschiedene Varianten eines Dreiecks mit der Höhe ein.
Teilaufgabe b)
In Teilaufgabe b) sollst du einen Punkt D angeben, sodass das Dreieck ABD einen doppelt so großen Flächeninhalt wie das Dreieck ABC hat. Das Dreieck ABD soll also folgenden Flächeninhalt $A_{Δ}^{'}$ haben:
$A_{Δ}^{'} = 2 \cdot A_{Δ} = 2 \cdot 4 {cm}^{2} = 8 {cm}^{2}$
Nun nutzt du wieder die Flächeninhaltsformel für Dreiecke. Auch hier kannst du $A B$ als Grundseite wählen. Bestimme die Höhe $h^{'}$ so , dass das Dreieck $A B D$ einen Flächeninhalt von $8 {cm}^{2}$ hat.
$A_{Δ}^{'}$ $=$ $\frac{1}{2} \cdot A B \cdot h^{'}$
↓
Setze $A B = 4 cm$ und $A_{Δ}^{'} = 8 {cm}^{2}$ ein.
$8 {cm}^{2}$ $=$ $\frac{1}{2} \cdot 4 cm \cdot h^{'}$
$8 {cm}^{2}$ $=$ $2 cm \cdot h^{'}$ $: 2 cm$
$4 cm$ $=$ $h^{'}$
Das Dreieck $A B D$ mit der Grundseite $A B$ muss also eine Höhe $h^{'} = 4 cm$ besitzen. Zeichne einen Punkt $D$ ein, der diese Bedingung erfüllt.
2
Entscheide, ob man aus folgenden Angaben eindeutig Dreiecke konstruieren kann.
Und wenn ja, konstruiere das Dreieck.
1. $c = 5 c m; α = 50^{\circ}; β = 60^{\circ}$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
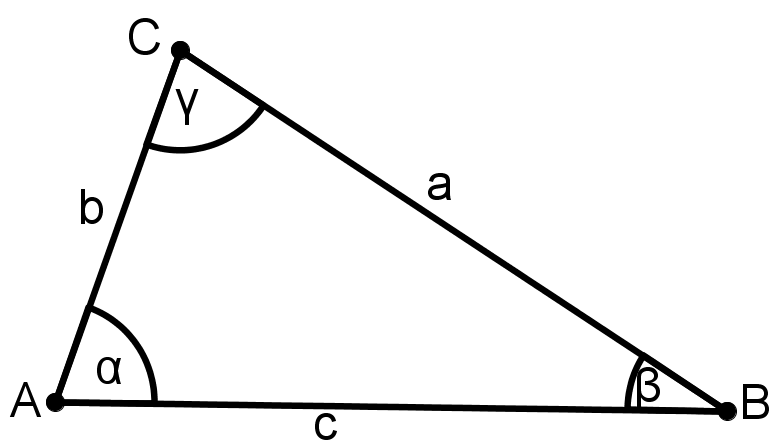
  Benenne ein beliebiges Dreieck
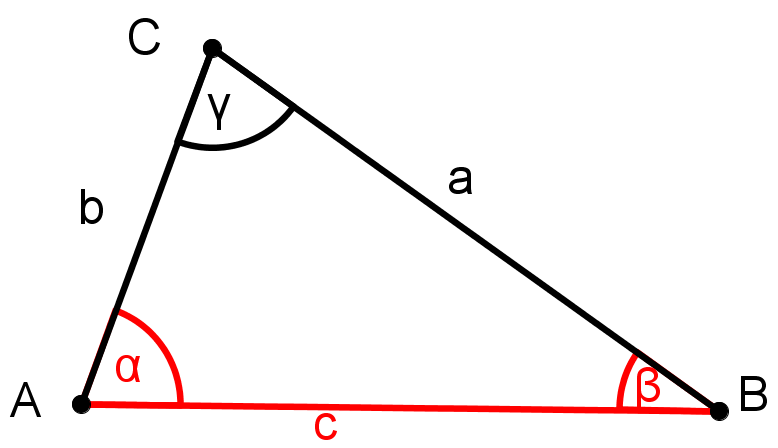
  Markiere die bekannten Größen. Man sieht in der Skizze, dass das Dreieck die Voraussetzung des WSW-Satzes erfüllt. Deshalb ist es eindeutig konstruierbar.
  Dreieck konstruieren
  Hier findest du das Applet zur Konstruktion mithilfe des WSW-Satzes.
  Zeichne eine Gerade und auf ihr irgendwo den Punkt A ein.
  Zeichne einen Kreis um A, dessen Radius genauso groß ist wie die Länge der Seite c.
  Der Schnittpunkt des Kreises mit der Geraden ist der Punkt B.
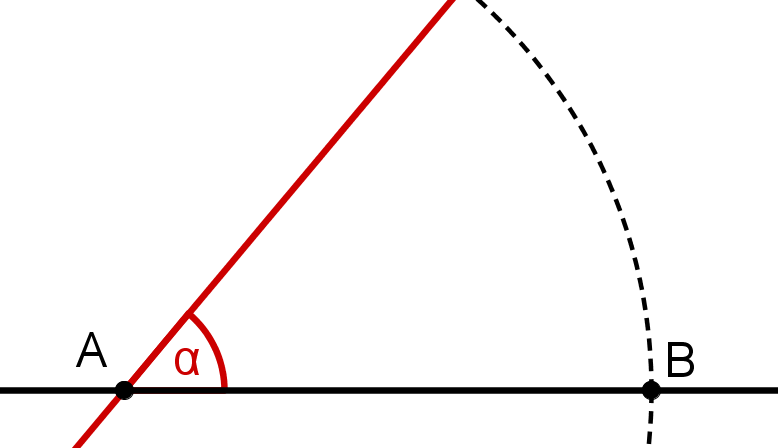
  Zeichne an A einen 50° Winkel.
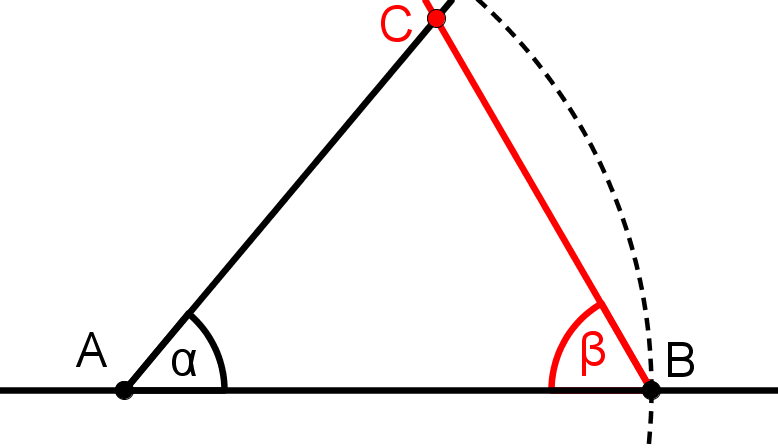
  Zeichne an B einen 60° Winkel.
  Der Schnittpunkt der beiden Schenkel ist der Punkt C des Dreiecks.
  Somit hat man das Dreieck eindeutig konstruiert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $a = 3 c m; b = 5 c m; γ = 30^{\circ}$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck
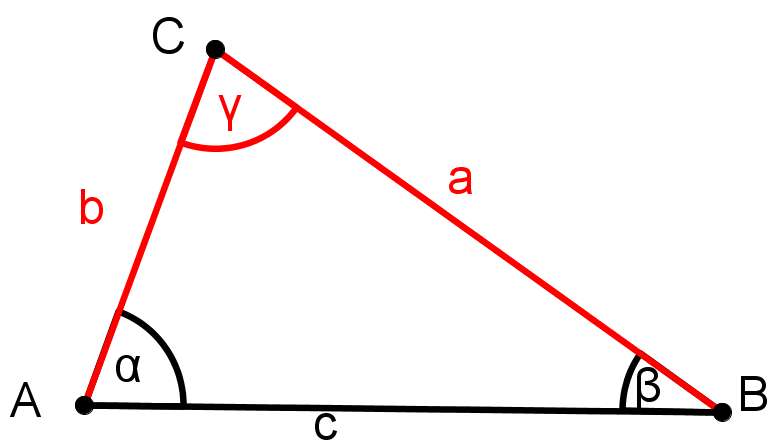
  Markiere die bekannten Größen.
  Man sieht in der Skizze, dass das Dreieck die Voraussetzung des SWS-Satzes erfüllt.
  Deshalb ist es eindeutig konstruierbar.
  Dreieck konstruieren
  Hier findest du ein Applet zur Konstruktion mithilfe des SWS-Satzes.
  Zeichne eine Gerade und auf ihr irgendwo den Punkt C ein.
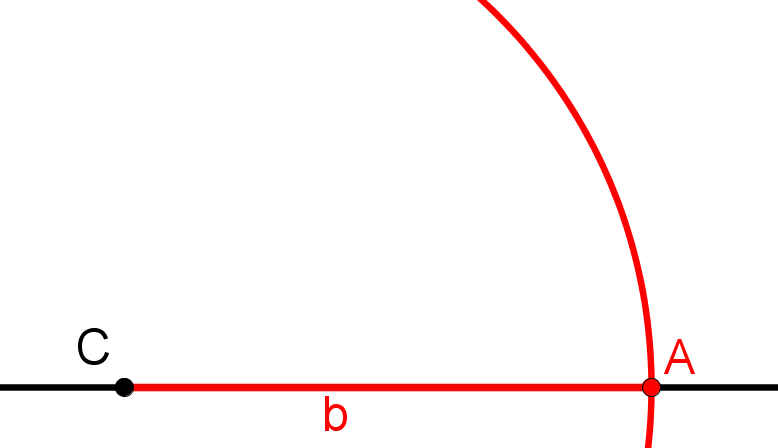
  Zeichne einen Kreis um C, dessen Radius genauso groß ist wie die Länge der Seite b.
  Der Schnittpunkt des Kreises mit der Geraden ist der Punkt A.
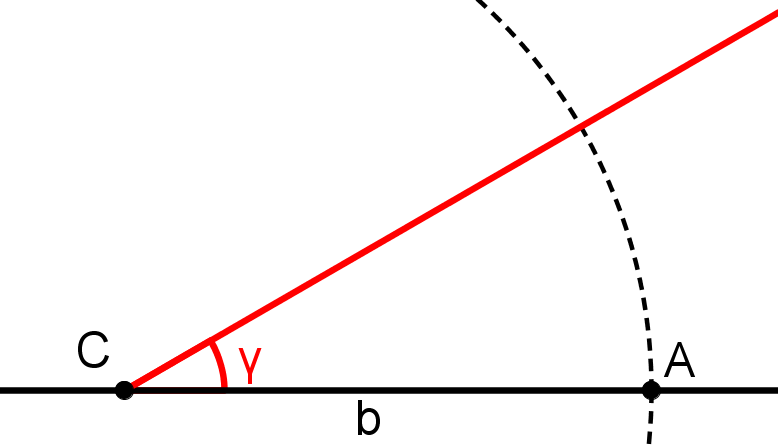
  Konstruiere an C einen 30° Winkel .
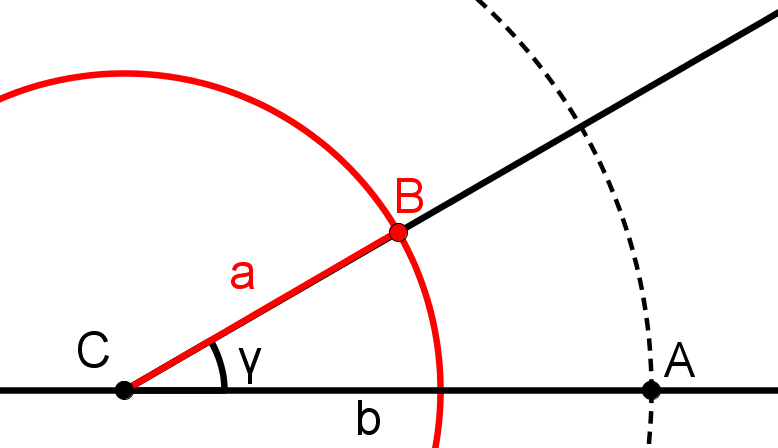
  Zeichne um C einen Kreis, dessen Radius so groß ist wie die Seite a.
  Der Schnittpunkt des Kreises mit dem eben konstruierten Schenkel ist der Punkt B.
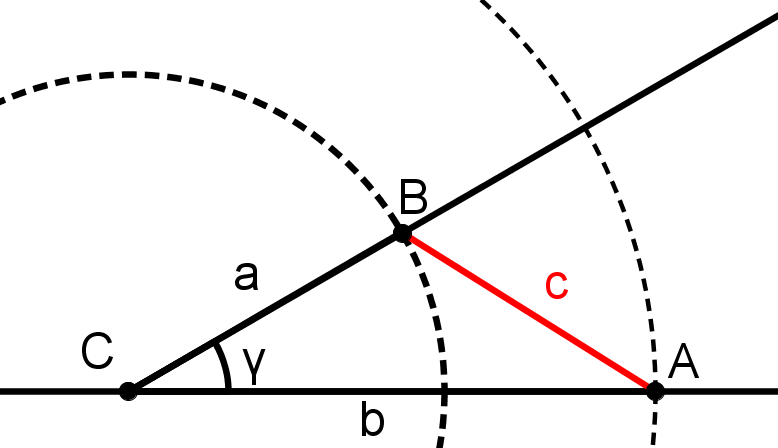
  Verbinde die Punkte A und B. Diese Strecke ist die Seite c.
  Das Dreieck ABC ist das gesuchte Dreieck.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $a = 5 cm; b = 4 cm; α = 45^{\circ}$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck und markiere die bekannten Größen.
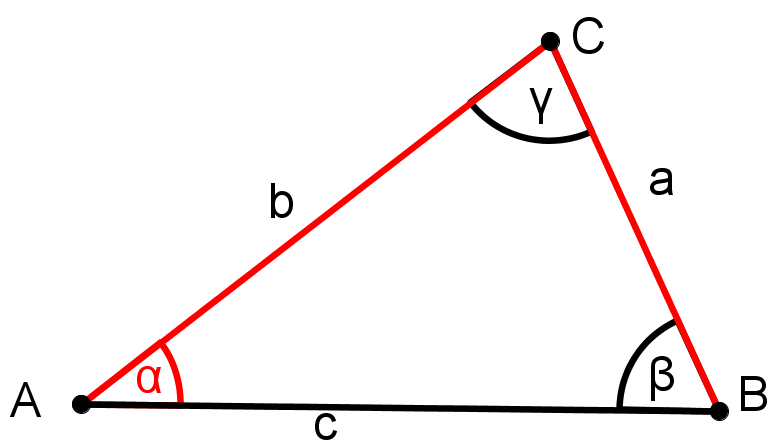
  Laut Skizze kommt nur der SsW-Satz in Frage. Es muss also noch überprüft werden, ob die Seite, die dem gegebenen Winkel gegenüberliegt größer ist als die andere Seite.
  Laut Angabe ist $a > b$ , weshalb die Voraussetzung des SsW-Satzes erfüllt ist.
  Deshalb ist es eindeutig konstruierbar.
  (VORSICHT: Würde man nur die Skizze betrachten, wäre $a < b$ )
  Dreieck konstruieren
  Hier findest du ein Applet zur Konstruktion mithilfe des SsW-Satzes.
  Zeichne einen Strahl von einem Punkt $A$ aus und konstruiere einen Winkel von $45^{\circ}$ mit dem Scheitel bei $A$ .
  Der Punkt $C$ liegt auf dem zweiten Schenkel des Winkels $4$ cm von $A$ entfernt.
  Zeichne einen Kreis um $C$ mit dem Radius $5$ cm. Der Schnittpunkt dieses Kreises mit dem Strahl von $A$ aus ist der Punkt $B .$
  Die Strecke AB ist die Seite c.
  Verbinde den Punkt $B$ mit dem Punkt $C$ . Diese Strecke ist die Seite $a$ .
  Das Dreieck $A B C$ ist das gesuchte Dreieck
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $a = 3 c m; b = 4 c m; c = 8 c m$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck
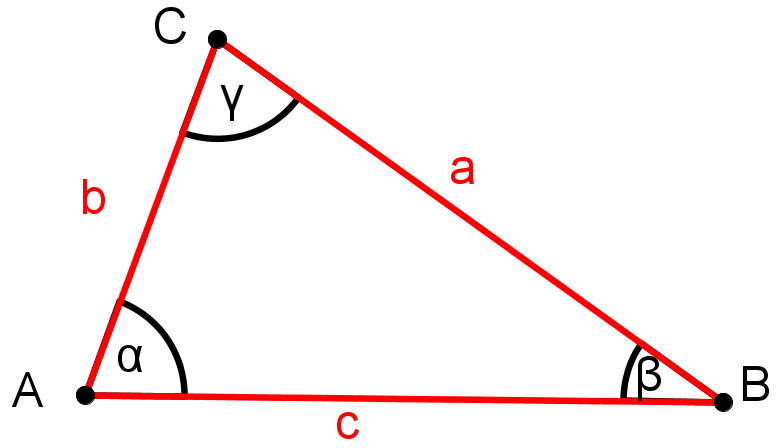
  Markiere die bekannten Größen.
  Man sieht in der Skizze, dass das Dreieck die Voraussetzung des SSS-Satzes erfüllt.
  Deshalb wäre es eindeutig konstruierbar.
  ABER:
  Artikel zum Thema
  Dreiecksungleichung überprüfen
  $a = 3 c m$
  $b = 4 c m$
  $a + b = 3 c m + 4 c m = 7 c m$
  aber:
  $c = 8 c m$
  $\to c > a + b$
  Da die Seite c größer als die Summe der anderen beiden Seiten ist, existiert dieses Dreieck nicht!
  Versucht man das Dreieck dennoch zu konstruieren (ohne die Dreiecksungleichung beachtet zu haben), stellt man fest, dass sich die Kreise die den Seiten a und b entsprechen nicht schneiden, es also kein Punkt C gibt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.