Vervollständige die Wertetabellen so, dass x und y zueinander …
… direkt proportional sind
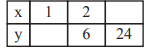
Zwei Größen sind dann direkt proportional zueinander, wenn die eine Größe aus der anderen hervorgeht, indem man sie mit immer dem gleichen Faktor multipliziert.
In der zweiten Werte Spalte der Tabelle sind die Werte für x und y beide gegeben. Wir suchen also einen Faktor z, mit dessen Hilfe sich der Wert für x aus dem Wert von y errechnen lässt. Dazu können wir folgende Formel verenden:
y = z⋅x ↓ Einsetzen der Werte für x und y
6 = z⋅2 ↓ auflösen nach z
z = 3 Damit haben wir den Faktor bestimmt und können die fehlenden Werte für die anderen Spalten berechnen.
1. Werte Spalte
y = z⋅x ↓ Einsetzen der bekannten Werte
y = 3⋅1 y = 3 y=3 ist der fehlende Wert in der ersten Werte Spalte.
3. Werte Spalte
y = z⋅x ↓ Einsetzen der bekannten Werte
24 = 3⋅x ↓ Auflösen nach x
x = 8 x=8 ist der fehlende Wert in der dritten Werte Spalte.
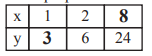
Vollständige Tabelle
Hast du eine Frage oder Feedback?
Wende die Bedingung für direkte Proportionalität an
… indirekt proportional sind
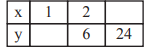
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Proportionalitäten
Zwei Größen sind dann indirekt proportional, wenn das Produkt zweier Größen immer konstant ist.
In der zweiten Werte Spalte der Tabelle sind die Werte für x und y beide gegeben. Wir suchen also einen Wert z, mit dessen Hilfe sich der Wert für x aus dem Wert von y errechnen lässt. Dazu können wir folgende Formel verenden:
z = x⋅y ↓ Einsetzen der bekannten Werte
z = 2⋅6 z = 12 Damit haben wir den Wert bestimmt und können die fehlenden Werte für die anderen Spalten berechnen.
1. Werte Spalte
z = x⋅y ↓ Einsetzen der bekannten Werte
12 = 1⋅y y = 12 y=12 ist der fehlende Wert in der ersten Werte Spalte.
3. Werte Spalte
z = x⋅y ↓ Einsetzen der bekannten Werte
12 = x⋅24 x = 0,5 x=0,5 ist der fehlende Wert in der dritten Werte Spalte.
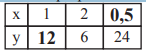
Vollständige Tabelle
Hast du eine Frage oder Feedback?
Wende die Bedingung für indirekte Proportionalität an
