Die Parabel verläuft durch die Punkte und . Sie hat eine Gleichung der Form mit und . Die Gerade hat die Gleichung mit .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeigen Sie durch Berechnung der Werte für b und c, dass die Parabel p die Gleichung hat.
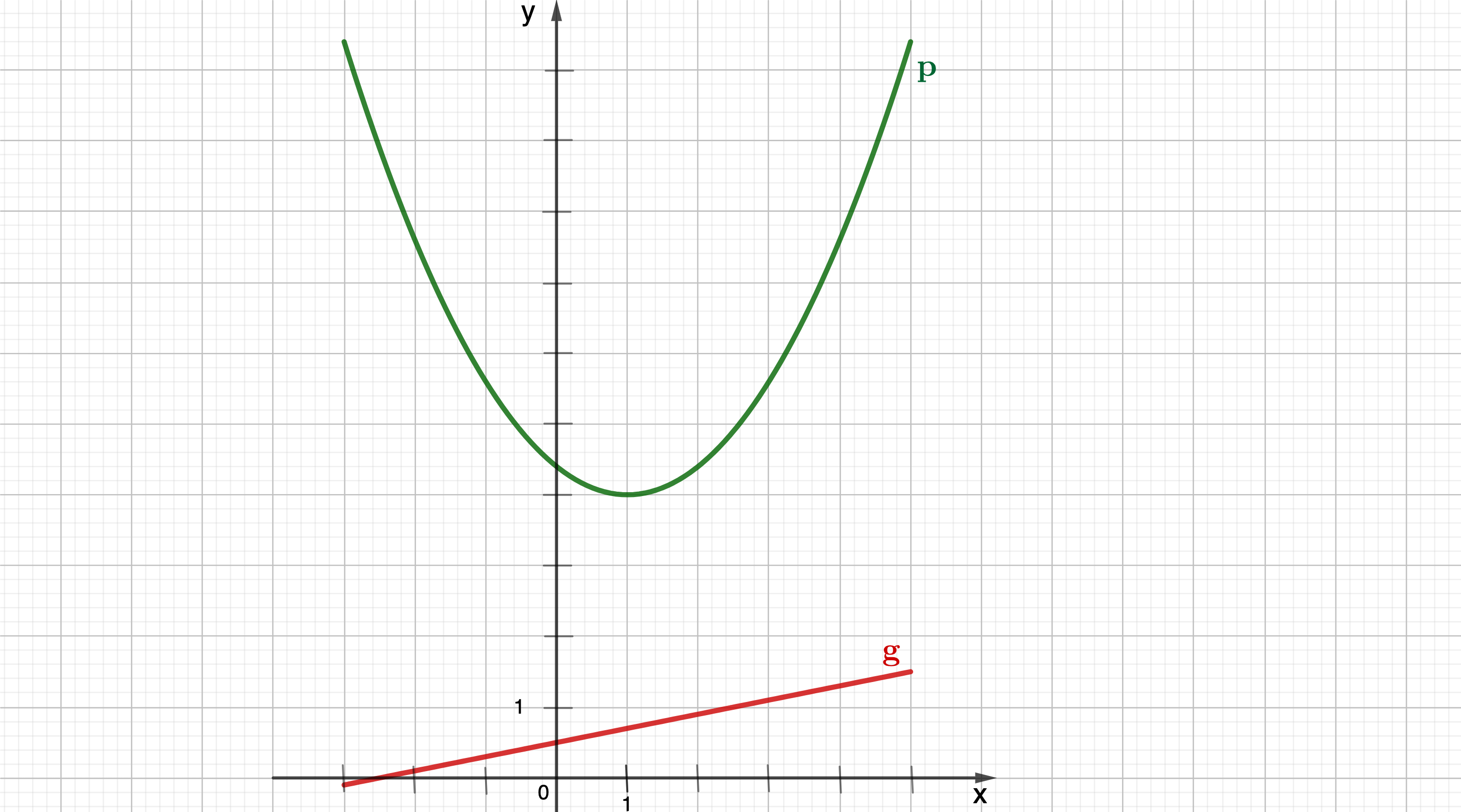
Zeichnen Sie sodann die Gerade g sowie die Parabel p für in ein Koordinatensystem ein.
Für die Zeichnung: Längeneinheit 1 cm;
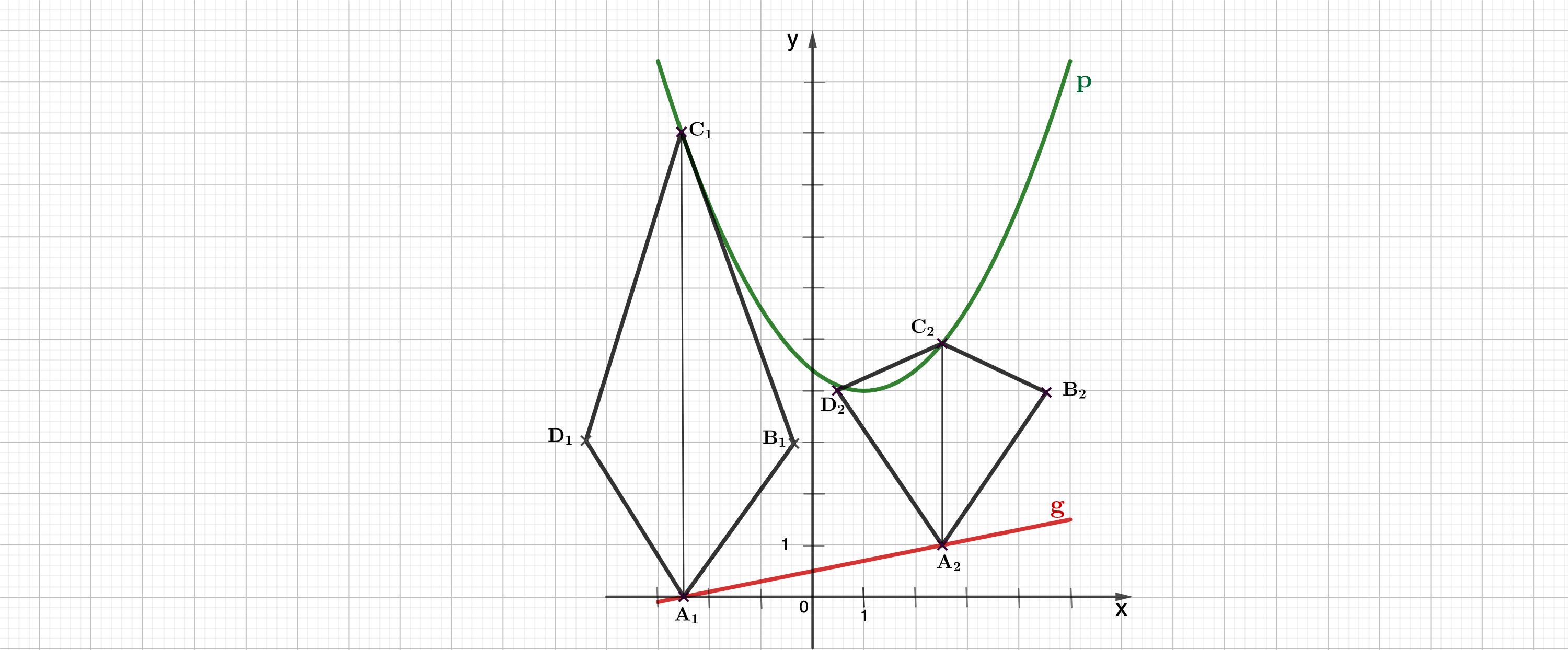
Punkte und sind zusammen mit Punkten auf der Geraden g und Punkten auf der Parabel p die Eckpunkte von Drachenvierecken mit den Geraden als Symmetrieachse.
Es gilt: .
Zeichnen Sie das Drachenviereck für und das Drachenviereck für in das Koordinatensystem zu Teilaufgabe (a) ein.
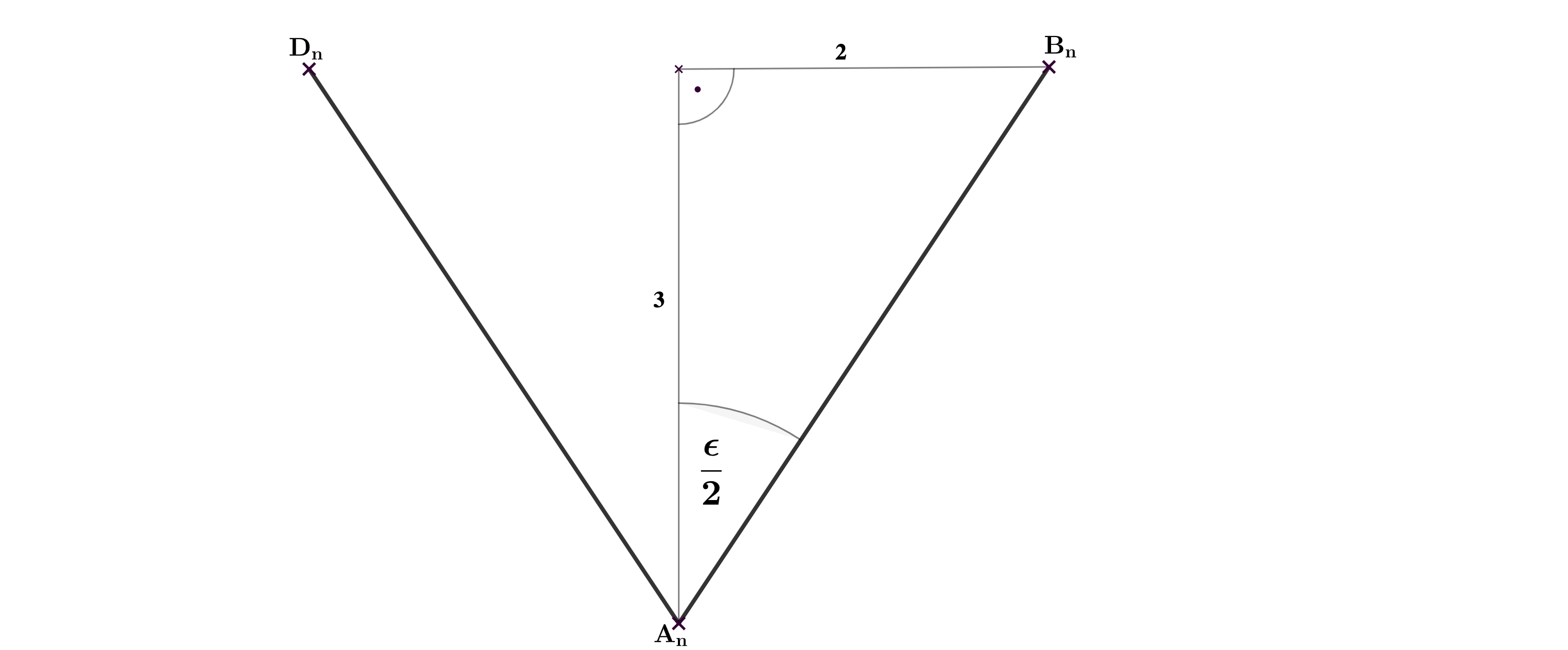
In allen Drachenvierecken haben die Winkel das gleiche Maß . Berechnen Sie das Maß der Winkel .
Zeigen Sie rechnerisch, dass für den Flächeninhalt A der Drachenvierecke in Abhängigkeit von der Abszisse x der Punkte gilt: [Teilergebnis: ]
Unter den Drachenvierecken hat das Drachenviereck den minimalen Flächeninhalt.
Berechnen Sie den Flächeninhalt des Drachenvierecks und den zugehörigen Wert für .
Begründen Sie, dass für die Drachenvierecke Rauten sind.
Ermitteln Sie die -Werte der Punkte und .
Zeigen Sie durch Rechnung, dass die Punkte und nicht gemeinsam auf einer Geraden liegen können.