Aufgabe 1C
Die Abbildung 1 zeigt schematisch die achsensymmetrische Seitenansicht einer Brücke.
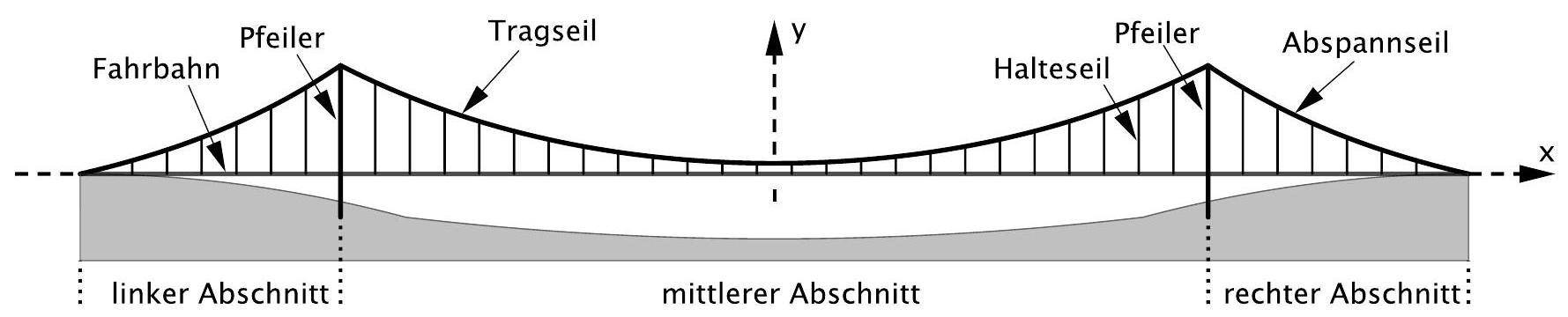
Die beiden vertikalen Pfeiler haben einen Abstand von . Am oberen Ende jedes Pfeilers ist sowohl das Tragseil des mittleren Abschnitts als auch das Abspannseil des linken bzw. rechten Abschnitts befestigt. Die beiden Abspannseile sind am jeweiligen Ende der Fahrbahn auf Fahrbahnhöhe verankert.
Im Koordinatensystem entspricht eine Längeneinheit in der Realität. In der Seitenansicht der Brücke verläuft die -Achse entlang der horizontal verlaufenden Fahrbahn, die -Achse entlang der Symmetrieachse.
Im rechten Abschnitt der Brücke wird der Verlauf des Abspannseils durch die Funktion mit beschrieben.
Zeigen Sie, dass die Fahrbahn der Brücke insgesamt lang ist. (4 BE)
Auch im linken Abschnitt der Brücke kann der Verlauf des Abspannseils durch einen Funktionsterm beschrieben werden.
Geben Sie einen passenden Term sowie das Intervall an, in dem dieser Term das Abspannseil darstellt. (3 BE)
Berechnen Sie die Länge eines Pfeilers oberhalb der Fahrbahn. (3 BE)
Berechnen Sie die Größe des Winkels, unter dem das rechte Abspannseil auf den rechten Pfeiler trifft. (4 BE)
In der Seitenansicht begrenzen der rechte Pfeiler, das Abspannseil und die Fahrbahn ein Flächenstück. Für eine Baumaßnahme wird zwischen Abspannseil und Fahrbahn eine Teilfläche des Flächenstücks mit einem Schutznetz verkleidet. Links wird die Teilfläche vom Pfeiler begrenzt und rechts endet sie mit einer vertikalen Begrenzung. Die Teilfläche soll halb so groß sein wie das gesamte Flächenstück.
Bestimmen Sie den Abstand der vertikalen Begrenzung zum Pfeiler. (6 BE)
Im Folgenden wird der mittlere Abschnitt betrachtet. Die 24 vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Sie haben von den Pfeilern und untereinander einen horizontalen Abstand von jeweils . Der Verlauf des Tragseils wird durch die Funktion s mit beschrieben.
Begründen Sie die Gültigkeit der folgenden Aussage: (2 BE)
Im Term von s ist erkennbar, dass die Seitenansicht der Brücke achsensymmetrisch ist.
Geben Sie die Bedeutung des Terms im Sachzusammenhang an:
Begründen Sie Ihre Angabe. (5 BE)
Punkt ist der Punkt auf dem rechten Pfeiler, der auf der Höhe der Fahrbahn liegt. Berechnen Sie den Abstand von zum Tragseil. (7 BE)
Die Punkte und werden in dieser Reihenfolge durch Strecken verbunden.
Berechnen Sie die Summe der Streckenlängen und begründen Sie, dass die Länge des Tragseils größer ist als die Summe der Streckenlängen in der Realität. (6 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen




