Wahlteil - GTR - lernen mit Serlo!

Aufgabe 2C

Ein Unternehmen stellt Tischtennisbälle her. $98 \%$ der hergestellten Bälle weichen nur unwesentlich von der Kugelform ab; diese werden im Weiteren als „rund“ bezeichnet, die übrigen als „unrund“. Aus der großen Menge der hergestellten Bälle werden regelmäßig Stichproben entnommen, wobei die Auswahl der Bälle für jede Stichprobe als zufällig angenommen werden kann. Außerdem kann davon ausgegangen werden, dass die Anzahl der unrunden Bälle in jeder Stichprobe binomialverteilt ist.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Anzahl unrunder Bälle in einer Stichprobe von 200 Bällen kleiner als der Erwartungswert dieser Anzahl ist. (3 BE)

Betrachtet werden zwei Stichproben von jeweils 200 Bällen. Berechnen Sie die Wahrscheinlichkeit dafür, dass in mindestens einer dieser beiden Stichproben mehr als sechs Bälle unrund sind. (3 BE)

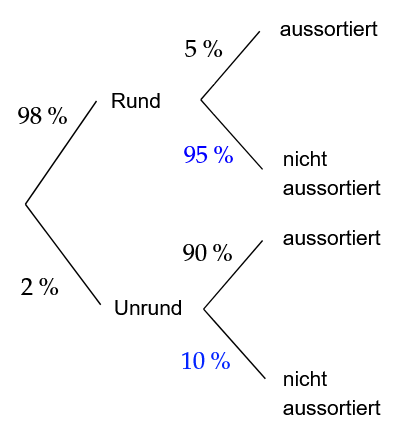
Nach der Herstellung durchlaufen die Bälle eine Sortieranlage. Dabei wird ein unrunder Ball mit einer Wahrscheinlichkeit von $90 \%$ aussortiert. Allerdings werden auch $5 \%$ der runden Bälle aussortiert.
Stellen Sie den Prozess der Herstellung und Sortierung der Bälle in einem beschrifteten Baumdiagramm dar. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Erste Stufe
Aus der Aufgabenstellung lassen sich die Wahrscheinlichkeiten der Ereignisse ablesen:
$98~\%$ der Bälle sind rund
$2~\%$ der Bälle sind unrund
Erste Stufe des Baumdiagramms
Zweite Stufe
In der zweiten Stufe werden die Ereignisse "aussortiert" und "nicht aussortiert" dargestellt.
Runde Bälle werden in $5~\%$ der Fälle aussortiert.
Unrunde Bälle werden in $90~\%$ der Fälle aussortiert.
Die blauen Wahrscheinlichkeiten lassen sich berechnen.
Die Wahrscheinlichkeiten der Ereignisse, die aus einem "Knoten" im Baumdiagramm kommen, ergeben zusammen immer $100~\%$ .
Vollständiges Baumdiagramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Skizziere die erste Stufe des Baumdiagramms mit den Ereignissen "rund" und "unrund".
Skizziere die zweite Stufe des Baumdiagramms mit den Angaben der Teilaufgabe (c).
Beschreiben Sie die Bedeutung des Terms $0{,}98 \cdot 0{,}05 \cdot 2000$ im Sachzusammenhang.
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Bedeutung des Terms
Die Faktoren $0{,}98 \cdot 0{,}05$ beschreiben die Wahrscheinlichkeit eines runden, aussortierten Balls.
Multipliziert man die Wahrscheinlichkeit mit einer Anzahl wie 2000, ergibt sie die zu erwartende Anzahl von runden, aussortierten Bällen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche die Faktoren und vergleiche mit den Wahrscheinlichkeiten aus den Teilaufgaben davor.
Stichwort: Erwartungswert

Angenommen, die nicht aussortierten Bälle würden die gleiche Sortieranlage ein zweites Mal durchlaufen.

Ermitteln Sie den Anteil der unrunden Bälle unter denjenigen, die dann nach zweimaligem Durchlaufen der Anlage nicht aussortiert würden. (4 BE)

Das Gewicht eines Tischtennisballs soll 2,70 Gramm (g) betragen. Das Gewicht der Bälle in der Produktion wird als normalverteilt angenommen mit $\mu=2{,}70$ und $\sigma=0{,}03$ . Bei der Qualitätskontrolle von Tischtennisbällen in der Produktion werden jeweils 24 Bälle getestet. Es gelten folgende Regeln:
I) Jedes Gewicht zwischen 2,67 $\mathrm{g}$ und 2,77 $\mathrm{g}$ ist akzeptabel, wobei einer der getesteten Bälle ein Gewicht außerhalb dieses Toleranzbereichs aufweisen darf.
II) Keiner der Bälle darf ein Gewicht von unter 2,60 g oder über 2,85 g aufweisen.
Bei der Qualitätskontrolle der Bälle gibt es Bereiche von Gewichten, in denen nach den Regeln I und II das Gewicht höchstens eines der Bälle liegen darf, ohne dass es zu einer Beanstandung bei der Kontrolle kommt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass das Gewicht eines zufällig ausgewählten Balles der Produktion innerhalb dieser Bereiche von Gewichten liegt.
(3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Wahrscheinlichkeit berechnen
Ein Gewicht zwischen $2{,}67$ g und $2{,}77$ g ist nicht zu beanstanden. Ein Ball darf mit seinem Gewicht außerhalb dieses Bereiches liegen, also in:
Mit dem Taschenrechner und der Normalverteilung mit den Parametern $\mu=2{,}70, ~\sigma=0{,}03$ gilt:
$P($ $2{,}6\le X\le2{,}67)=0{,}1582$
$P(2{,}77\le X\le2{,}85)=0{,}0098$
Dabei steht $X$ für das normalverteilte Gewicht des Balls. Zusammen ist die Wahrscheinlichkeit:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verwende die Normalverteilung mit den Parametern $\mu=2{,}70$ und $\sigma=0{,}03$ .
Bestimme die Wahrscheinlichkeit mit dem TR, dass das Gewicht des Balls in den Bereichen $[2{,}6;2{,}67]$ oder $[2{,}77;2{,}85]$ liegt.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass bei einer Qualitätskontrolle von 24 Bällen keine Beanstandung aufgrund von Regel I auftritt. (4 BE)

Durch Einstellung der Produktionsmaschine kann der Wert für $\mu$ verändert werden. Der Wert von $\sigma$ bleibt dabei unverändert.
Entscheiden Sie, ob $\mu=2{,}70$ die optimale Einstellung der Maschine ist und begründen Sie Ihre Entscheidung. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
Entscheidung und Begründung
Nein, die Einstellung ist nicht optimal.
Das Gewicht der "meisten" Bälle liegt um den Erwartungswert verteilt. Darum sollte dieser mittig im Intervall $[2{,}67;2{,}77]$ liegen: $\Rightarrow\mu=2{,}72$
Damit wäre die Wahrscheinlichkeit maximiert, dass das Gewicht der Bälle in $[2{,}67;2{,}77]$ liegt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche die Normalverteilung und den Erwartungswert.
Wo müsste dieser im optimalen Fall liegen, so dass die Wahrscheinlichkeit für den Bereich $[2{,}67;2{,}77]$ maximal ist?

$\displaystyle \mu$	$=$	$\displaystyle n\cdot p$
	↓	$n=200,~p=0{,}02$ ( $2~\%$ der Bälle sind unrund)
	$=$	$\displaystyle 200\cdot0{,}02$
	$=$	$\displaystyle 4$

Umformuliert
	↓
$\displaystyle P\left(X<4\right)$	$=$	$\displaystyle P\left(X\le3\right)$
	↓	Verteilungsfunktion
	$=$	$\displaystyle F_{200;0{,}02}\left(3\right)$
	↓	Taschenrechner (BinomialCDF)
	$≈$	$\displaystyle 0{,}4315$

Verwende das Gegenereignis
	↓
$\displaystyle P(X>6)$	$=$	$\displaystyle 1-P\left(X\le6\right)$
	↓	Verteilungsfunktion der Binomialverteilung
	$=$	$\displaystyle 1-F_{200;0{,}02}\left(6\right)$
	↓	Taschenrechner (BinomialCDF)
	$≈$	$\displaystyle 1-0{,}8914$
	$≈$	$\displaystyle 0{,}1086$

	$\displaystyle 1-\left(P\left(X\le6\right)\right)^2$
	↓ Einsetzen der Wahrscheinlichkeit
$=$	$\displaystyle 1-0{,}8914^2$
$≈$	$\displaystyle 0{,}2054$

	$\displaystyle \frac{P(\text{unrund, zwei mal nicht aussortiert})}{P(\text{aussortiert})}$
	↓ Baumdiagramm
$=$	$\displaystyle \frac{0{,}02\cdot0{,}1\cdot0{,}1}{0{,}98\cdot0{,}95\cdot0{,}95+0{,}02\cdot0{,}1\cdot0{,}1}$
$≈$	$\displaystyle 0{,}00023$

Aufgabe 2C

Erwartungswert der Stichprobe

Wahrscheinlichkeit $P(X < 4)$

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit $P(X>6)$

Wahrscheinlichkeit für die Stichproben

Hast du eine Frage oder Feedback?

Erste Stufe

Zweite Stufe

Hast du eine Frage oder Feedback?

Bedeutung des Terms

Hast du eine Frage oder Feedback?

Relativer Anteil

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit berechnen

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit, dass das Gewicht in $[2{,}67;2{,}77]$ liegt

Hast du eine Frage oder Feedback?

Entscheidung und Begründung

Hast du eine Frage oder Feedback?

	$\displaystyle P\left(\text{Regel I erfüllt}\right)$
	↓ Teilaufgabe (g)
$=$	$\displaystyle \underbrace{0{,}8315^{24}}_{\text{Alle Bälle in [2{,}67;2{,}77]}}+\underbrace{0{,}8315^{23}\cdot 0{,}1680\cdot 24}_{\text{Ein Ball in [2{,}60;2{,}67] }\cup~[2{,}77;2{,}85]}$
$=$	$\displaystyle 0{,}07$

Aufgabe 2C

Erwartungswert der Stichprobe

Wahrscheinlichkeit P(X<4)P(X < 4)P(X<4)

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit P(X>6)P(X>6)P(X>6)

Wahrscheinlichkeit für die Stichproben

Hast du eine Frage oder Feedback?

Erste Stufe

Zweite Stufe

Hast du eine Frage oder Feedback?

Bedeutung des Terms

Hast du eine Frage oder Feedback?

Relativer Anteil

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit berechnen

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit, dass das Gewicht in [2,67;2,77][2{,}67;2{,}77][2,67;2,77] liegt

Hast du eine Frage oder Feedback?

Entscheidung und Begründung

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit $P(X < 4)$

Wahrscheinlichkeit $P(X>6)$

Wahrscheinlichkeit, dass das Gewicht in $[2{,}67;2{,}77]$ liegt