Wahlteil - GTR

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben zur Abiturprüfung eA 2022, Wahlteil - GTR. Zum Download hier.

1
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 1A
Gegeben ist die Schar der in $ℝ$ definierten Funktionen $f_{a}$ mit $f_{a} (x) = x \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}}$
mit $a \in ℝ$ . Die zugehörigen Graphen sind symmetrisch bezüglich des Koordinatenursprungs.
Es gilt: $f_{a}^{'} (x) = (1 - a \cdot x^{2}) \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}}$
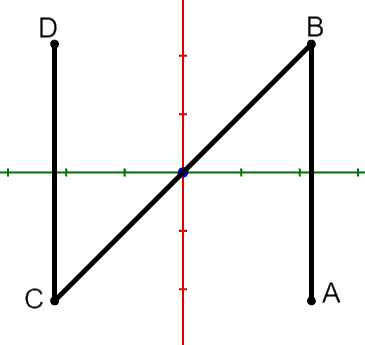
1. Zeigen Sie, dass $f_{1}$ genau eine Nullstelle hat. Abbildung 1 zeigt den Graphen von $f_{1}$ ohne das zugrunde liegende Koordinatensystem.
  Ergänzen Sie die Koordinatenachsen und skalieren Sie diese passend. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
  Berechnen der Nullstelle
  $f_{1} (x) = x \cdot e^{- \frac{1}{2} x^{2} + \frac{1}{2}}$
  $f_{1} (x) = 0 \Rightarrow 0 = x \cdot e^{- \frac{1}{2} x^{2} + \frac{1}{2}}$
  Da für alle $x$ gilt: $e^{- \frac{1}{2} x^{2} + \frac{1}{2}} \neq 0$ bleibt nur die Lösung $x = 0$ .
  $f_{1}$ hat genau eine Nullstelle bei $x = 0$ .
  Weitere Eigenschaften:
  Wegen $f (- x) = - f (x)$ ist der Graph von $f_{1}$ punktsymmetrisch zum Koordinatenursprung.
  Der Graph nähert sich rechts und links asymptotisch an die x-Achse an. Es gilt: $\lim_{x \to \pm \infty} f_{1} (x) = 0$
  Es ist $f_{1}^{'} (x) = Ableitung (f_{1}) = e^{- \frac{1}{2} x^{2} + \frac{1}{2}} (1 - x^{2})$ . $f_{1}^{'} (x) = 0$ für $x = \pm 1$ .
  Gemäß der Abbildung hat der Graph bei $x = 1$ einen $H P$ mit der y-Koordinate $f_{1} (1) = 1 \cdot e^{0} = 1$ $\Rightarrow H P (1 | 1)$ und wegen der Punktsymmetrie einen $T P (- 1 | - 1)$ .
  Graph von $f$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für die Nullstelle:
  Setze $f_{1} (x) = 0$ .
  Für die Skalierung:
  Beachte $f (- x) = - f (x)$ . Was folgt daraus?
  Wie verläuft der Graph für $x \mapsto \pm \infty$ ?
  Wo befindet sich z.B. der Hochpunkt $H P$ ?
2. Interpretieren Sie den folgenden Sachverhalt geometrisch:
  Für jede Stammfunktion $F_{1}$ von $f_{1}$ und für jede reelle Zahl $u > 2022$ gilt: (3 BE)
  $F_{1} (u) - F_{1} (0) \approx \int_{0}^{2022} f_{1} (x) d x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion, Integral und Flächenberechnung
  Sachverhalt analysieren
  Für jede Stammfunktion $F_{1}$ von $f_{1}$ und für jede reelle Zahl $u > 2022$ gilt:
  $F_{1} (u) - F_{1} (0) \approx \int_{0}^{2022} f_{1} (x) d x$
  Für jede Zahl $u > 2022$ schließen der Graph von $f_{1}$ , die x-Achse und die Gerade $x = u$ ein bestimmtes Flächenstück ein. Dieses Flächenstück ist ungefähr so groß, wie der Flächeninhalt, den der Graph von $f_{1}$ mit der x-Achse und der Geraden $x = 2022$ einschließt.
  Ab $u > 2022$ kommt sozusagen keine nennenswerte Fläche mehr durch das Integral dazu. Das liegt an der asymptotischen Annäherung des Graphen an die $x$ -Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es werden zwei Flächeninhalte miteinander vergleichen, welche sind das?
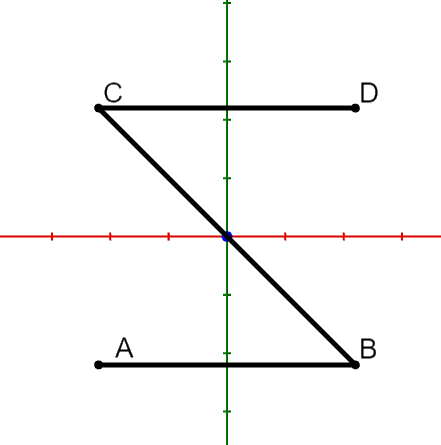
3. Begründen Sie unter Verwendung der
  Abbildung 2, dass gilt: (3 BE)
  $\int_{- 0,5}^{1} f_{- 1} (x) d x = \int_{0,5}^{1} f_{- 1} (x) d x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Begründung
  $\int_{- 0,5}^{1} f_{- 1} (x) d x = \int_{0,5}^{1} f_{- 1} (x) d x$
  $f_{- 1}$ ist punktsymmetrisch zum Koordinatenursprung. Deshalb ist $| \int_{- 0,5}^{0} f_{- 1} (x) d x | = \int_{0}^{0,5} f_{- 1} (x) d x$ .
  Die linke Teilfläche liegt aber unterhalb der x-Achse, sodass $\int_{- 0,5}^{0,5} f_{- 1} (x) d x = 0$ ist. Es bleibt nur der Inhalt der Teilfläche im Intervall $[0,5; 1]$ übrig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte: $f_{- 1}$ ist punktsymmetrisch zum Koordinatenursprung.
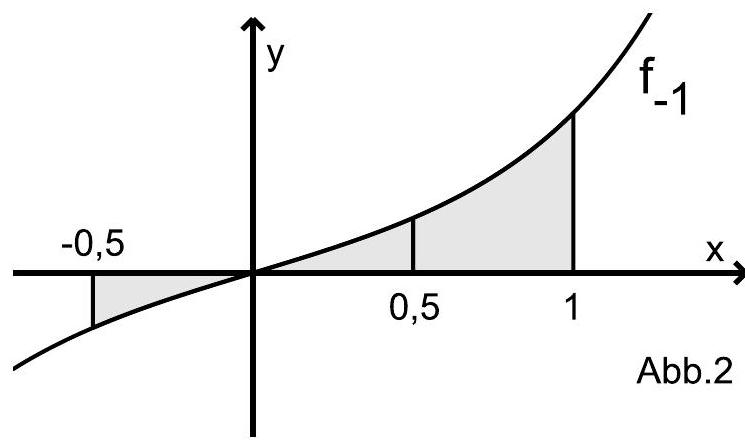
4. Für einen Wert von $a$ liegt der Punkt $P (1 | e)$ auf dem Graphen von $f_{a}$ .
  Berechnen Sie für diesen Wert von $a$ die Größe des Winkels, den der Graph von $f_{a}$ mit der Parallele zur $x$ -Achse durch den Punkt $P$ einschließt. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Berechnung von $a$
  Für $x = 1$ ist $f_{a} (1) = e$ :
  $e$ $=$ $e^{- \frac{1}{2} a \cdot 1^{2} + \frac{1}{2}}$
  $e^{1}$ $=$ $e^{- \frac{1}{2} a + \frac{1}{2}}$
  Vergleiche die Exponenten: $1 = - \frac{1}{2} a + \frac{1}{2} \Rightarrow \frac{1}{2} = - \frac{1}{2} a \Rightarrow a = - 1$
  Berechnung des Winkels, den der Graph von $f_{a}$ mit der Parallelen zur $x$ -Achse durch den Punkt $P$ einschließt
  Gegeben ist $f_{a}^{'} (x) = (1 - a \cdot x^{2}) \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}}$ .
  Dann ist $f_{- 1}^{'} (x) = e^{- \frac{1}{2} (- 1) \cdot x^{2} + \frac{1}{2}} (1 - (- 1) \cdot x^{2}) = e^{\frac{1}{2} \cdot x^{2} + \frac{1}{2}} (1 + x^{2})$
  Für $x = 1$ ist dann $f_{- 1}^{'} (1) = e^{\frac{1}{2} \cdot 1^{2} + \frac{1}{2}} (1 + 1^{2}) = e^{1} \cdot 2$
  Für den Winkel gilt dann: $φ = \tan^{- 1} (2 e) \approx 80^{\circ}$ .
  Der Graph von $f_{a}$ schließt mit der Parallelen zur $x$ -Achse durch den Punkt $P$ einen Winkel von etwa $80^{\circ}$ ein.
  Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.
  Sie dient nur der Veranschaulichung.
  Abbildung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Löse $f_{a} (1) = e$ nach $a$ auf.
  Teil 2
  Berechne die Steigung $f_{- 1}^{'} (1)$ .
  Für den Winkel gilt dann: $φ = \tan^{- 1} (f_{- 1}^{'} (1))$
5. Die folgenden Aussagen gelten für alle reellen Zahlen $a, a_{1}$ und $a_{2}$ :
  $f_{a} (0) = 0$
  $f_{a_{1}} (x) = f_{a_{2}} (x)$ gilt genau dann, wenn $a_{1} = a_{2}$ oder $x = 0$ ist.
  Geben Sie an, was sich aus diesen Aussagen jeweils für den Verlauf der Graphen der Schar folgern lässt. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
  Verlauf der Graphen
  $f_{a} (0) = 0$ $\Rightarrow$ Alle Graphen der Schar gehen durch den Ursprung $(0 | 0)$ .
  $f_{a_{1}} (x) = f_{a_{2}} (x) \Leftrightarrow a_{1} = a_{2}$ oder $x = 0$ $\Rightarrow$ Die Graphen für verschiedenes $a$ haben nur bei $x = 0$ einen gemeinsamen Punkt. Wenn sich zwei Graphen außer für $x = 0$ noch an einer anderen Stelle schneiden, dann müssen die Graphen identisch sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Untersuche nacheinander die zwei Aussagen.
  Aussagen über $f$ betreffen die Lage des Graphen im Koordinatensystem.
  Aussagen über $f^{'}$ betreffen die Steigung.
6. Für alle Werte von $a \neq 0$ stimmen die Wendestellen von $f_{a}$ mit den Lösungen
  der Gleichung $(a \cdot x^{2} - 3) \cdot x = 0$ überein. Es ist $f_{0} (x) = x \cdot e^{\frac{1}{2}}$ .
  Klassifizieren Sie die Anzahl der Wendestellen von $f_{a}$ nach dem Wert von $a \in ℝ$ . (7 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Anzahl der Wendestellen von $f_{a}$ nach dem Wert von $a \in ℝ$
  Für $a = 0$ ist $f_{0} (x) = x \cdot e^{\frac{1}{2}}$ eine Gerade, die keinen Wendepunkt hat.
  Für $a \neq 0$ gilt für die Wendestellen $(a \cdot x^{2} - 3) \cdot x = 0$ mit den Lösungen:
  $x = 0$ oder $x^{2} = \frac{3}{a}$
  Ist $a < 0$ , dann hat die Gleichung für die Wendestellen genau eine Lösung und der Graph $f_{a}$ hat genau eine Wendestelle.
  Ist $a > 0$ , dann hat die Gleichung für die Wendestellen genau drei Lösungen und der Graph $f_{a}$ hat genau drei Wendestellen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Fälle $a = 0; a < 0$ und $a > 0$ .
7. Zeigen Sie, dass die folgende Aussage für jeden Wert von a richtig ist:
  Wird der Graph von $f_{a}$ mit dem gleichen Faktor $k > 0$ sowohl in $x$ -Richtung als auch in $y$ -Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen stauchen und strecken
  Der entstehende Graph
  Streckung in y-Richtung: $k \cdot f_{a} (x)$
  Streckung in x-Richtung: $f_{a} (\frac{x}{k})$
  Ausführung beider Streckungen $(k > 0) \Rightarrow k \cdot f_{a} (\frac{x}{k})$
  $k \cdot f_{a} (\frac{x}{k}) = k \cdot \frac{x}{k} \cdot e^{- \frac{1}{2} a \cdot {(\frac{x}{k})}^{2} + \frac{1}{2}} = x \cdot e^{- \frac{1}{2} \frac{a}{k^{2}} \cdot x^{2} + \frac{1}{2}} = f_{\frac{a}{k^{2}}} (x)$
  Der entstandene Graph $f_{\frac{a}{k^{2}}}$ ist ebenfalls eine Funktion der Schar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Streckung in y-Richtung: $k \cdot f_{a} (x)$
  Streckung in x-Richtung: $f_{a} (\frac{x}{k})$
  Wende beide Streckungen nacheinander auf $f_{a}$ an.
8. Beschreiben Sie die Lage der Punkte $(x | y)$ mit $x \cdot y < 0$ im Koordinatensystem und begründen Sie, dass keiner dieser Punkte auf einem Graphen der Schar liegt. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadranten im Koordinatensystem
  Lösung
  Keiner dieser Punkte liegt auf einem Graphen der Schar
  Die Punkte $(x | y)$ mit $x \cdot y < 0$ liegen im Innern des 2. und 4. Quadranten.
  Für $x < 0$ muss $y > 0$ sein $\Rightarrow$ 2. Quadrant.
  Für $x > 0$ muss $y < 0$ sein $\Rightarrow$ 4. Quadrant.
  $f_{a} (x) = x \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}}$ $\Rightarrow$ für alle $x$ ist $e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}} > 0$
  Damit ist $f_{a} (x) < 0$ für $x < 0$ und $f_{a} (x) > 0$ für $x > 0$ .
  Die Graphen der Schar liegen also im Innern des 1. und 3. Quadranten und damit liegen keine Punkte $(x | y)$ mit $x \cdot y < 0$ auf einem Graphen der Schar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege, wo die Punkte $(x | y)$ mit $x \cdot y < 0$ liegen.
  Überlege, in welchen Quadranten die Graphen von $f_{a}$ liegen.
9. Alle Extrempunkte der Graphen der Schar liegen auf einer Geraden. Begründen Sie, dass es sich dabei um die Gerade mit der Gleichung $y = x$ handelt. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Begründung, dass es sich dabei um die Gerade mit der Gleichung $y = x$ handelt
  Löse die Gleichung $f_{a}^{'} (x) = 0$ .
  $0 = (1 - a \cdot x^{2}) \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}} \Rightarrow$ nur die Klammer kann null werden.
  Du erhältst die Lösungen $x_{1,2} = \pm \sqrt{\frac{1}{a}}$ .
  Berechne zunächst $f_{a} (+ \sqrt{\frac{1}{a}})$
  $f_{a} (x)$ $=$ $x \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}}$
  ↓
  Setze $x = + \sqrt{\frac{1}{a}}$ ein.
  $f_{a} (+ \sqrt{\frac{1}{a}})$ $=$ $+ \sqrt{\frac{1}{a}} \cdot e^{- \frac{1}{2} a \cdot {(+ \sqrt{\frac{1}{a}})}^{2} + \frac{1}{2}}$
  ↓
  Vereinfache die Potenz.
  $=$ $+ \sqrt{\frac{1}{a}} \cdot e^{- \frac{1}{2} a \cdot (\frac{1}{a}) + \frac{1}{2}}$
  ↓
  Kürze in der Potenz.
  $=$ $+ \sqrt{\frac{1}{a}} \cdot e^{- \frac{1}{2} + \frac{1}{2}}$
  $=$ $+ \sqrt{\frac{1}{a}} \cdot e^{0}$
  ↓
  Es ist $e^{0} = 1$ .
  $=$ $+ \sqrt{\frac{1}{a}}$
  Entsprechend erhält man für $f_{a} (- \sqrt{\frac{1}{a}}) = - \sqrt{\frac{1}{a}}$
  Für beide Extrema gilt jeweils, dass der x-Wert gleich dem Funktionswert ist. Die $x$ - und $y$ -Koordinaten sind gleich. Alle Extrema liegen somit auf der Geraden mit der Gleichung $y = x$ .
  Hinweis: Nur zur Veranschaulichung (In der Aufgabenstellung nicht gefordert.)
  Drei Scharkurven mit der Ortskurve $y = x$ der Extrema.
  Skizze der Graphen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Gleichung $f_{a}^{'} (x) = 0$ $\Rightarrow x_{1,2}$
  Berechne dann $f_{a} (x_{1})$ bzw. $f_{a} (x_{2})$ .
10. Für jeden positiven Wert von $a$ bilden der Hochpunkt ( $v | v)$ des Graphen von $f_{a}$ , der Punkt $(0 | 2)$ , der Koordinatenursprung und der Punkt $(v | 0)$ die Eckpunkte eines Vierecks.
  Bestimmen Sie ausgehend von einer geeigneten Skizze denjenigen Wert von $a$ , für den das Viereck den Flächeninhalt 144 hat. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Berechne den Wert von $a$ , für den das Viereck den Flächeninhalt 144 hat
  Für die Skizze wird die in Aufgabe a) verwendete Abbildung $1$ , die mit Koordinatenachsen versehen wurde und skaliert ist, benutzt.
  Skizze
  Das Viereck stellt ein Trapez dar. Die Flächenformel für das Trapez lautet:
  $A_{Trapez} = \frac{1}{2} \cdot (a + c) \cdot h$
  Nach der obigen Skizze hat die Seite $a$ die Länge $2$ , die Seite $c$ die Länge $f_{a} (v) = v$ und die Höhe $h$ hat die Länge $v$ .
  Eingesetzt in die Flächenformel erhält man:
  $A_{Trapez} = \frac{1}{2} \cdot (2 + v) \cdot v$
  Dieser Flächeninhalt soll $144$ sein. Löse die Gleichung $\frac{1}{2} \cdot (2 + v) \cdot v = 144$ .
  Für $v > 0$ erhältst Du die Lösung $v = 16$ und damit ist $f_{a} (16) = 16$ .
  Der GTR liefert als Lösung dieser Gleichung $a \approx 0,003906...$ .
  Für $a \approx 0,0039$ hat das Viereck den Flächeninhalt $144$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Fertige eine Skizze an.
  Das Viereck stellt ein Trapez dar.
  Die Flächenformel für das Trapez lautet: $A_{Trapez} = \frac{1}{2} \cdot (a + c) \cdot h$
  Setze die entsprechenden Werte für $a, c$ und $h$ ein und löse die Gleichung $A_{Trapez} = 144$ .
  Mit dem erhaltenen Wert $v > 0$ löse $f_{a} (v) = v$ nach $a$ auf.
2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 1B
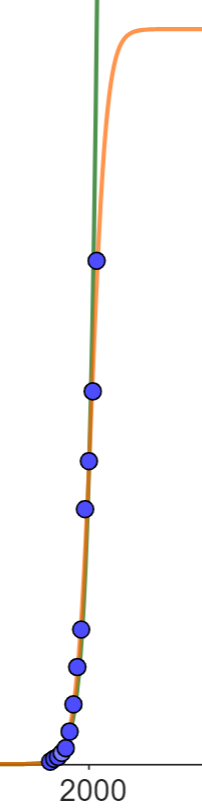
Die Grafik stellt den Schuldenstand Deutschlands in Mrd. Euro jeweils zu Beginn des Jahres ab dem Jahr 1950 dar.
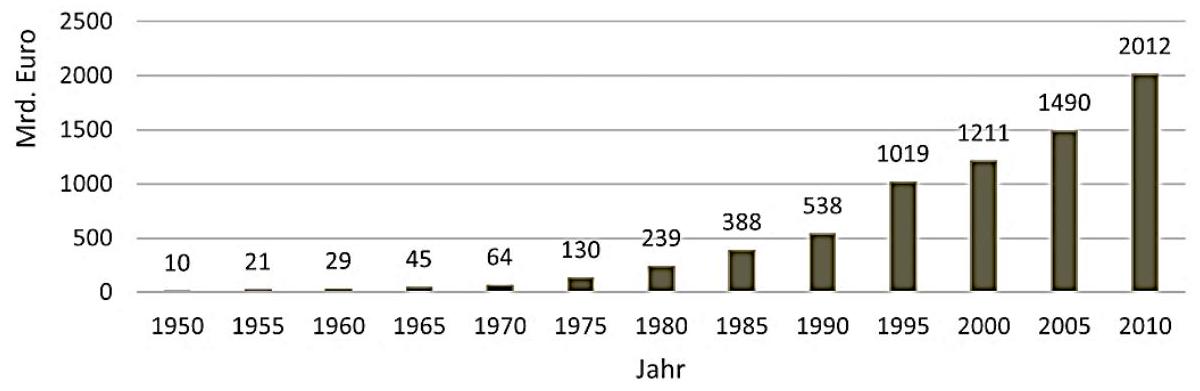
1. Geben Sie die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Diagramme erfassen und auswerten
  Fünfjahreszeiträume
  Dem Diagramm entnimmt man die erste Jahreszahl $1950$ mit $10$ Milliarden €.
  $1955$ hat sich der Schuldenstand auf $21$ Milliarden € erhöht, also etwas mehr als verdoppelt.
  Im weiteren Verlauf findet man dann das Jahr $1970$ mit $64$ Milliarden € und nach $5$ Jahren, also $1975$ einen Schuldenstand von $130$ Milliarden €, also etwas mehr als verdoppelt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte benachbarte Datensätze, bei denen einer etwa doppelt so groß wie der vorherige ist.
2. Bestimmen Sie zwei geeignete Regressionsfunktionen.
  Beurteilen Sie die von Ihnen gewählten Regressionsfunktionen hinsichtlich ihrer Eignung zur Beschreibung des vorliegenden Sachverhalts. (9 BE)
  
  Exponentielle Regression
  Wähle z.B. die exponentielle Regression $y = a \cdot e^{b \cdot x}$ .
  Übertrage alle Daten in eine Tabelle und lass Dir die entsprechenden Koeffizienten anzeigen.
  Der TR liefert die Werte $a \approx 1,15085 \cdot 10^{- 76}$ und $b \approx 1,09522$
  $\Rightarrow y = 1,15085 \cdot 10^{- 76} \cdot e^{1,09522 \cdot x}$
  Ergebnis ist eine klassische e-Funktion mit unbegrenztem Schuldenwachstum. Es findet keine Schuldenbremse statt.
  Logistische Regression
  Wähle als weitere Möglichkeit die logistische Regression $y = \frac{c}{1 + a \cdot e^{- b \cdot x}}$ .
  Der TR liefert die Werte $c \approx 2938,15971$ , $a \approx 4,33448 \cdot 10^{89}$ und $b \approx 0,10303$
  $\Rightarrow y = \frac{2938,15971}{1 + 4,33448 \cdot 10^{89} \cdot e^{- 0,10303 \cdot x}}$
  Ergebnis ist eine sich abflachende e-Funktion, die geeignet ist, den Schuldenstand mit einer Schuldenbremse darzustellen.
  Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.
  Sie dient nur der Veranschaulichung.
  Die blauen Punkte sind der gegebene Datensatz. Der grüne Graph entspricht der exponentiellen Regression und der orangefarbige Graph der logistischen Regression.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Übertrage die Daten in eine Tabelle.
  Wähle z.B. die exponentielle Regression $y = a \cdot e^{b \cdot x}$ .
  Wähle als weitere Möglichkeit die logistische Regression $y = \frac{c}{1 + a \cdot e^{- b \cdot x}}$
  Lasse Dir vom TR die entsprechenden Parameter ausrechnen und interpretiere beide Ergebnisse bezüglich einer möglichen Schuldenbremse.
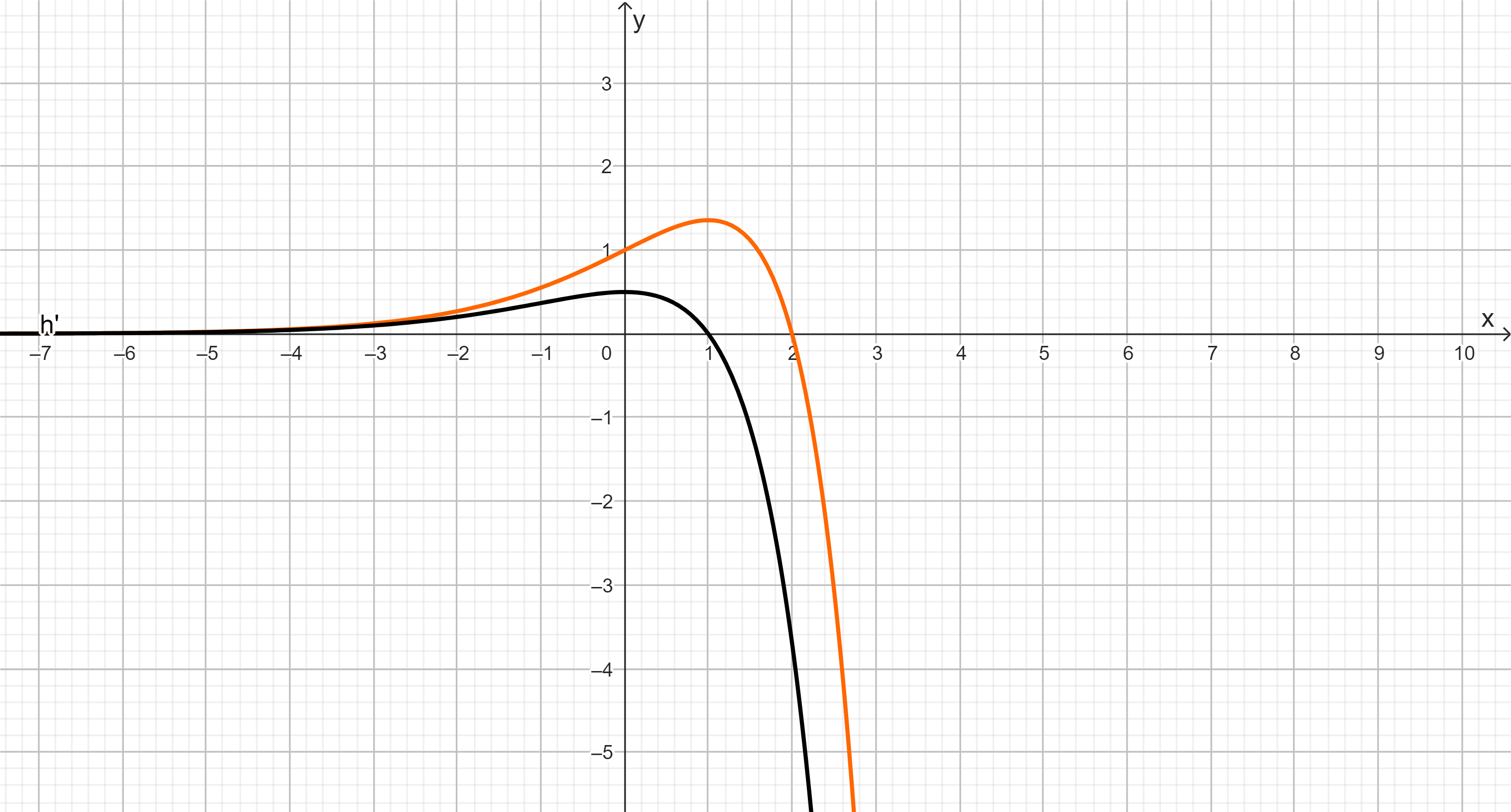
3. In einem Modell soll der Anstieg des Schuldenstands gestoppt werden und die Schulden sollen abgebaut werden. Zu Beginn des Jahres 2005 beträgt der Schuldenstand in diesem Modell 1490 Mrd. Euro. Die Änderungsrate des Schuldenstands soll ab Beginn des Jahres 2005 durch die Funktion $g$ mit $g (x) = 235 \cdot e^{- 0,25 x} - 35$ , $x$ in Jahren ab dem Jahr 2005, $g (x)$ in Mrd. Euro pro Jahr, beschrieben werden. Die Abbildung zeigt den Graphen der Funktion $g$ . Eine Stammfunktion zu $g$ lautet:
  $G (x) = - 940 \cdot e^{- 0,25 x} - 35 \cdot x$
  Begründen Sie, dass der nach diesem Modell erwartete Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 mit dem folgenden Term bestimmt werden kann: (3 BE)
  $1490 + \int_{0}^{20} g (x) d x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
  Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 kann mit dem folgenden Term bestimmt werden: $1490 + \int_{0}^{20} g (x) d x$
  Die Funktion $𝑔$ gibt die Änderung des Schuldenstands in Milliarden € pro Jahr an.
  Das Integral von $𝑔$ über ein Zeitintervall gibt die Gesamtzunahme der
  Schulden in dem entsprechenden Zeitraum an.
  $1490$ Milliarden € ist der Schuldenstand zu Beginn des Jahres $2005$ .
  Das Integral geht von $0$ (entspricht dem Jahr $2005$ ) bis $20$ (entspricht dem Jahr $2025$ ).
  Die Summe von $1490$ und dem Integral gibt demnach den Schuldenstand zu Beginn des Jahres $2025$ an.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Funktion $𝑔$ gibt die Änderung des Schuldenstands in Milliarden € pro Jahr an.
  Das Integral von $𝑔$ über ein Zeitintervall gibt die Gesamtzunahme der Schulden in dem entsprechenden Zeitraum an.
  Interpretiere dann die angegebene Summe.
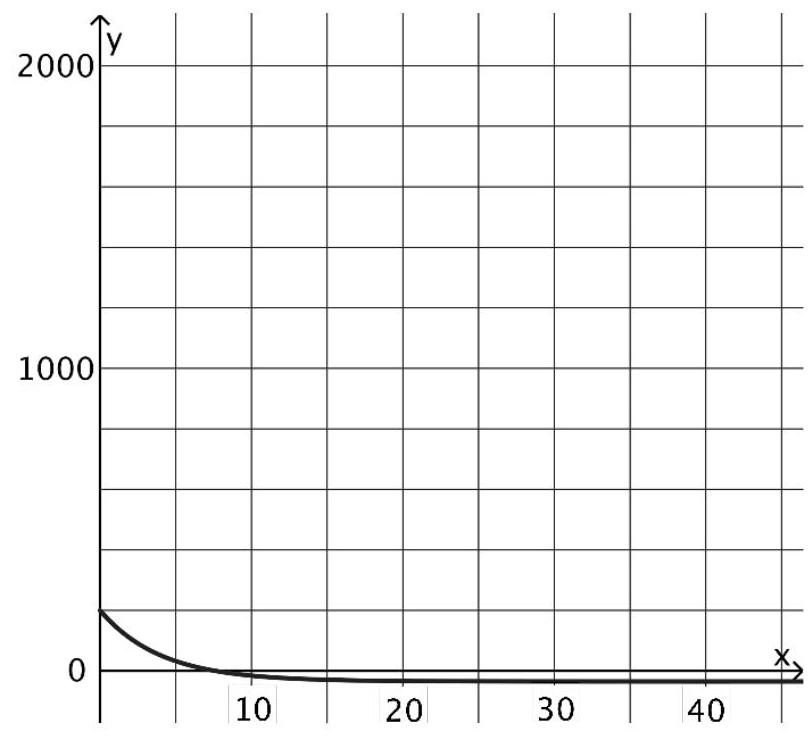
4. Skizzieren Sie in das Koordinatensystem den nach diesem Modell ungefähr zu erwartenden Schuldenstand vom Beginn des Jahres 2005 bis zum Jahr 2045. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Skizze des Koordinatensystems
  Der Schnittpunkt mit der y-Achse liegt bei $1490$ .
  Der Hochpunkt liegt an der Stelle der Nullstelle des Graphen von $𝑔$ .
  Nach dem Hochpunkt erfolgt annähernd eine lineare Abnahme.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Schnittpunkt mit der y-Achse liegt bei $1490$ .
  Der Hochpunkt liegt an der Stelle der Nullstelle des Graphen von $𝑔$ .
  Nach dem Hochpunkt erfolgt annähernd eine lineare Abnahme.
5. Berechnen Sie für dieses Modell das Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005. (4 BE)
  
  Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005
  Definiere die Funktion $f (x) = 1490 + \int_{0}^{t} g (x) d x$
  Löse dann die Gleichung $f (x) = 1490$ :
  $1490 + \int_{0}^{t} g (x) d x = 1490 \Rightarrow \int_{0}^{t} g (x) d x = 0$
  Der GTR liefert als Lösung $t \approx 26,824284...$ .
  Das Ergebnis ist $t \approx 26,8$ Jahre, d.h. wir sind dann im Jahr $2005 + 26,8 = 2031,8$ .
  Im Jahr $2031$ ist der zu erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres $2005$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Definiere die Funktion $f (x) = 1490 + \int_{0}^{t} g (x) d x$
  Löse dann die Gleichung $f (x) = 1490$ .
6. Bestimmen Sie den maximalen Schuldenstand sowie das Jahr, in dem dieser erreicht wird. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Maximaler Schuldenstand sowie das Jahr, in dem dieser erreicht wird
  Der Schuldenstand ist maximal, wenn die Änderungsrate gleich null ist.
  $g (x) = 235 \cdot e^{- 0.25 x} - 35 = 0$
  Der GTR liefert als Lösung dieser Gleichung den Wert $x \approx 7,616949...$ .
  Das Ergebnis ist $x \approx 7,62$ Jahre.
  Wir sind dann im Jahr $2005 + 7,62 = 2012,62$ .
  Im Jahr $2012$ ist der zu erwartete Schuldenstand maximal.
  Er beträgt $f (7,62) = 1490 + \int_{0}^{7,62} g (x) d x \approx 2023,4$
  Der maximale Schuldenstand beträgt etwa $2023,4$ Milliarden €.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für das Jahr des maximalen Schuldenstandes berechne $g (x) = 0 \Rightarrow x_{1} .$
  Für den maximalen Schuldenstand berechne $f (x_{1}) = 1490 + \int_{0}^{x_{1}} g (x) d x .$
7. Unabhängig vom Sachkontext ist die in $ℝ$ definierte Funktionenschar $h_{a}$ mit $h_{a} (x) = (1 - a \cdot x) \cdot e^{2 \cdot a \cdot x}, a \in ℝ$ , gegeben.
  Ohne weiteren Nachweis können Sie verwenden: $h_{a}^{'} (x) = a \cdot (1 - 2 \cdot a \cdot x) \cdot e^{2 \cdot a \cdot x}$
  Zeigen Sie für $a \neq 0$ , dass der maximale Funktionswert unabhängig vom Wert von $a$ ist.
  (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Nachweis für $a \neq 0$ , dass der maximale Funktionswert unabhängig vom Wert von $a$ ist
  Setze $h_{a}^{'} (x) = 0 \Rightarrow 0 = a \cdot (1 - 2 a x) \cdot e^{2 a x}$
  Mit dem Satz vom Nullprodukt folgt dann, dass $1 - 2 a x = 0$ sein muss, da $a \neq 0$ und $e^{2 a x} > 0$ für alle $x$ ist.
  $1 - 2 a x = 0 \Rightarrow x = \frac{1}{2 a}$
  Berechne den maximalen Funktionswert an der Stelle $x = \frac{1}{2 a}$ :
  $h_{a} (x)$ $=$ $(1 - a \cdot x) \cdot e^{2 \cdot a \cdot x}$
  ↓
  Setze $x = \frac{1}{2 a}$ ein.
  $h_{a} (\frac{1}{2 a})$ $=$ $(1 - a \cdot \frac{1}{2 a}) e^{2 a \cdot \frac{1}{2 a}}$
  ↓
  Kürze mit $a$ .
  $=$ $(1 - \frac{1}{2}) e^{\frac{2}{2}}$
  ↓
  Fasse zusammen.
  $=$ $\frac{1}{2} \cdot e^{1}$
  Der maximale Funktionswert $h_{a} (x) = \frac{1}{2} \cdot e$ ist unabhängig von $a$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $h_{a}^{'} (x) = 0 \Rightarrow x_{1}$
  Berechne $h_{a} (x_{1})$ .
8. Für jeden Wert von $a$ für $a \neq 0$ wird die Gerade durch den Schnittpunkt mit der $x$ -Achse und den Hochpunkt des zugehörigen Graphen zu $h_{a}$ betrachtet.
  Für alle diese Geraden gilt: Sie schneiden sich in einem Punkt auf der $y$ -Achse.
  Bestimmen Sie die $y$ -Koordinate dieses gemeinsamen Punktes auch mithilfe einer Skizze ohne Berechnung der Geradengleichungen. (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz (Vierstreckensatz)
  y-Koordinate dieses gemeinsamen Punktes mithilfe einer Skizze ohne Berechnung der Geradengleichungen
  Die Gerade geht durch den Schnittpunkt mit der $x$ -Achse und den Hochpunkt $H P (\frac{1}{2 a} | \frac{1}{2} e)$ des zugehörigen Graphen zu $h_{a}$ .
  Benötigt wird der Schnittpunkt mit der $x$ -Achse.
  Berechne $h_{a} (x) = 0$
  $0 = (1 - a x) \cdot e^{2 \cdot a \cdot x}$
  Wegen $e^{2 a x} > 0$ für alle $x$ , muss $1 - a x = 0$ sein $\Rightarrow x = \frac{1}{a}$
  Damit ergibt sich folgende Skizze:
  Gerade durch Extrema
  Aus der Skizze ist ersichtlich, dass die Strecke $| \frac{1}{a} |$ doppelt so lang wie die Strecke $| \frac{1}{2 a} |$ ist.
  Mit den Strahlensätzen ist dann auch der y-Achsenabschnitt doppelt so lang wie die Strecke $| \frac{1}{2} e |$ .
  Die $y$ -Koordinate dieses gemeinsamen Punktes auf der y-Achse ist dann gleich $e$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle eine Skizze mit dem Hochpunkt $H P (\frac{1}{2 a} | \frac{1}{2} e)$ und dem Schnittpunkt mit der $x$ -Achse. Berechne dazu $h_{a} (x) = 0 \Rightarrow x_{1} .$
  Vergleiche $x_{1}$ mit $\frac{1}{2 a}$ und $\frac{1}{2} e$ mit dem y-Achsenabschnitt der Geraden durch den Hochpunkt und dem Schnittpunkt mit der $x$ -Achse.
9. Berechnen Sie alle Werte von $a$ , für die der Graph der Ableitungsfunktion $h_{a}^{'}$ vollständig unterhalb oder oberhalb des Graphen der Funktion $h_{a}$ liegt. (5 BE)
  
  Werte von $a$ , für die der Graph der Ableitungsfunktion $h_{a}^{'}$ vollständig unterhalb des Graphen der Funktion $h_{a}$ liegt
  Es ist $h_{a} (x) = (1 - a x) \cdot e^{2 \cdot a \cdot x}$ und $h_{a}^{'} (x) = a \cdot (1 - 2 a x) \cdot e^{2 a x}$ .
  Berechne $h_{a} (x) = h_{a}^{'} (x)$ :
  $(1 - a x) \cdot e^{2 \cdot a \cdot x}$ $=$ $a \cdot (1 - 2 a x) \cdot e^{2 a x}$
  $1 - a x$ $=$ $a \cdot (1 - 2 a x)$
  ↓
  Löse die Klammer auf.
  $1 - a x$ $=$ $a - 2 a^{2} x$ $+ a x - a$
  $1 - a$ $=$ $a x - 2 a^{2} x$
  ↓
  Klammere $a x$ aus.
  $1 - a$ $=$ $x a (1 - 2 a)$
  Die Gleichung kann nur nach $x$ aufgelöst werden, nur wenn $a (1 - 2 a) \neq 0$ , d.h. $a \neq 0$ und $(1 - 2 a) \neq 0$ .
  Man erhält keine Lösung für $a = 0$ und für $1 - 2 a = 0 \Rightarrow a = \frac{1}{2}$ .
  Es ist $a = 0 \Rightarrow h_{0} (x) = 1$ und $h_{0}^{'} (x) = 0$ , d.h. $h_{0}^{'} (x)$ liegt ganz unterhalb von $h_{0} (x)$ .
  Es ist $a = \frac{1}{2} \Rightarrow$ $h_{\frac{1}{2}} (x) = (1 - \frac{1}{2} x) \cdot e^{2 \cdot \frac{1}{2} \cdot x} = (1 - \frac{1}{2} x) \cdot e^{x} = e^{x} - \frac{1}{2} x e^{x}$ und $h_{\frac{1}{2}}^{'} (x) = \frac{1}{2} \cdot (1 - 2 \frac{1}{2} x) \cdot e^{2 \frac{1}{2} x} = \frac{1}{2} \cdot (1 - x) \cdot e^{x} = \frac{1}{2} e^{x} - \frac{1}{2} x e^{x}$
  Damit liegt $h_{\frac{1}{2}}^{'} (x)$ stets unterhalb von $h_{\frac{1}{2}} (x)$ , weil $\frac{1}{2} e^{x}$ stets kleiner als $e^{x}$ ist.
  Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.
  Sie dient nur der Veranschaulichung.
  Graphen der Funktionen h und h'
  Dabei ist $h_{\frac{1}{2}}^{'} (x)$ der schwarze Graph und $h_{\frac{1}{2}} (x)$ der orangefarbige Graph.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $h_{a} (x) = h_{a}^{'} (x)$ .
  Suche die Werte für $a$ , für die die obige Gleichung keine Lösung hat.
3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 1C
Ein ICE fährt bis 15: 00 Uhr mit konstanter Geschwindigkeit. Von 15: 00 Uhr bis 15: 02 Uhr nimmt seine Geschwindigkeit ab. Ab 15: 02 Uhr fährt der ICE wieder mit konstanter Geschwindigkeit.
Die Geschwindigkeit von 15: 00 Uhr bis 15: 02 Uhr wird mithilfe der in $ℝ$ definierten Funktion $f$ mit $f (x) = 30 x^{3} - 90 x^{2} + 240$ beschrieben.
Dabei ist $x$ die seit 15: 00 Uhr vergangene Zeit in Minuten und $f (x)$ die Geschwindigkeit in Kilometer pro Stunde. Abbildung 1 veranschaulicht den Sachverhalt.
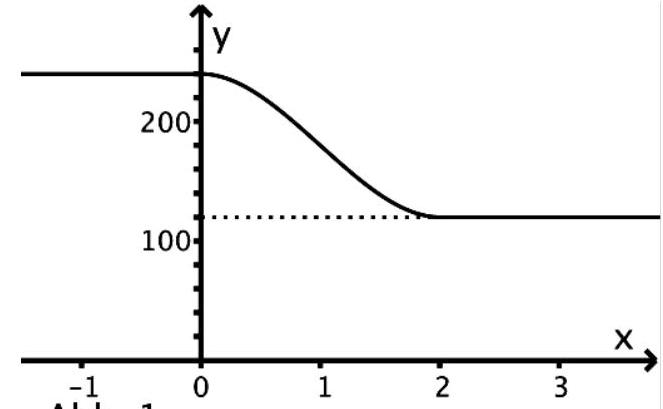
1. Bestimmen Sie die Geschwindigkeit, die der ICE eine halbe Minute nach 15: 00 Uhr hat.
  Zeigen Sie, dass die Geschwindigkeit in der ersten halben Minute nach 15: 00 Uhr um einen kleineren Betrag abnimmt als in der darauf folgenden halben Minute. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Geschwindigkeit, die der ICE eine halbe Minute nach 15: 00 Uhr hat.
  Berechne $f (0,5) = 30 \cdot {0,5}^{3} - 90 \cdot {0,5}^{2} + 240 = 221,25$
  Die Geschwindigkeit beträgt rund $221 \frac{km}{h}$ .
  Nachweis, dass die Geschwindigkeit in der ersten halben Minute nach 15: 00 Uhr um einen kleineren Betrag abnimmt als in der darauf folgenden halben Minute
  Berechne die Differenz der Geschwindigkeiten zum Zeitpunkt $x = 0$ und $x = 0,5$ und vergleiche mit der Differenz der Geschwindigkeiten zum Zeitpunkt $x = 0,5$ und $x = 1$ .
  Es ergeben sich folgende Funktionswerte: $f (0) = 240; f (0,5) = 221,5; f (1) = 180$
  Dann folgt für die Differenzen:
  $f (0) - f (0,5) = 240 - 221,25 = 18,75$
  $f (0,5) - f (1) = 221,25 - 180 = 41,25$
  Dabei ist $41,25 > 18,75$ , d.h. die Geschwindigkeit nimmt in der ersten halben Minute nach 15: 00 Uhr um einen kleineren Betrag ab als in der darauf folgenden halben Minute.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne $f (0,5)$ .
  Teil 2
  Berechne $f (0) - f (0,5)$ und $f (0,5) - f (1)$ und vergleiche.
2. Bestimmen Sie die Länge des Zeitraumes, in dem die Geschwindigkeit höchstens 200 aber mindestens 150 Kilometer pro Stunde beträgt. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Länge des Zeitraumes, in dem die Geschwindigkeit höchstens 200, aber mindestens 150 Kilometer pro Stunde beträgt
  Löse die Gleichung $f (x) = 200$ mit dem Ergebnis $x_{1} \approx 0,7739$ und die Gleichung $f (x) = 150$ mit dem Ergebnis $x_{2} \approx 1,3473$ .
  Die Differenz der beiden Zeiten ist dann $x_{2} - x_{1} \approx 0,5734$
  Die Länge des Zeitraumes, in dem die Geschwindigkeit höchstens $200$ , aber mindestens $150$ Kilometer pro Stunde beträgt, ist etwa $0,57$ Minuten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Gleichung $f (x) = 200$ mit dem Ergebnis $x_{1}$ und die Gleichung $f (x) = 150$ mit dem Ergebnis $x_{2}$ .
  Die Differenz der beiden Zeiten $x_{2} - x_{1}$ ist dann die Länge des gesuchten Zeitraums.
3. Geben Sie mögliche Werte $x_{1}$ und $x_{2}$ an, sodass gilt: $f^{'} (x_{1}) = f^{'} (x_{2})$ . Deuten Sie die Aussage $f^{'} (x_{1}) = f^{'} (x_{2})$ im Sachzusammenhang. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
  Mögliche Werte $x_{1}$ und $x_{2}$ an, sodass gilt: $f^{'} (x_{1}) = f^{'} (x_{2})$
  Lasse Dir die Ableitung von $f$ anzeigen: $y = \frac{d}{d x} (f (x))$
  Im Intervall $[0; 2]$ ist diese Parabel achsensymmetrisch zu $x = 1$ .
  Gleiche Ableitungswerte findet man dann an den Stellen, an denen $x_{1}$ und $x_{2}$ den gleichen Abstand zu 1 haben, z.B. bei $x_{1} = 1 - 0,5 = 0,5$ und $x_{2} = 1 + 0,5 = 1,5$ .
  Also ist $f^{'} (0,5) = f^{'} (1,5)$ .
  Aussage $f^{'} (x_{1}) = f^{'} (x_{2})$ im Sachzusammenhang
  Die momentanen Änderungsraten der Geschwindigkeiten sind zu den
  Zeitpunkten $x_{1}$ und $x_{2}$ identisch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lasse Dir die Ableitung von $f$ anzeigen.
  Die Parabel ist achsensymmetrisch $x = x_{S}$ .
  Gleiche Ableitungswerte findet man dann an den Stellen, an denen $x_{1}$ und $x_{2}$ den gleichen Abstand zu $x_{S}$ haben.
4. Ermitteln Sie den Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt.
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt
  Die stärkste Abnahme findet an der Stelle statt, an der $f^{'} (x)$ minimal wird.
  Das ist für $x = 1$ im Scheitel der Parabel der Fall.
  Der Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt, liegt bei $15 : 01$ Uhr.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die stärkste Abnahme findet an der Stelle statt, an der $f^{'} (x)$ minimal wird.
5. Bestimmen Sie einen Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15: 03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau $7 k m$ zurücklegt.
  (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
  Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15: 03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau $7 k m$ zurücklegt
  Die Geschwindigkeit ist in $\frac{km}{h}$ gegeben. Für eine Streckenberechnung, mit einer Zeit in Minuten, muss die Geschwindigkeit umgerechnet werden: $\frac{km}{h} \mapsto \frac{1}{60} \frac{km}{min}$
  Die zurückgelegte Strecke ist dann $s (t) = \frac{1}{60} \int_{0}^{t} f (x) d x$ .
  Die Geschwindigkeit von $15 : 00$ Uhr bis $15 : 02$ Uhr wird mithilfe der Funktion $f$ beschrieben. Die in diesen $2$ Minuten zurückgelegte Strecke wird dann durch das Integral berechnet: $s (2) = \frac{1}{60} \int_{0}^{2} f (x) d x = 6$
  Nach $2$ Minuten wurden $6$ km zurückgelegt. Da die zurückgelegte Strecke aber genau $7$ km sein soll, muss noch die Zeit berechnet werden, in der der ICE mit der konstanten Geschwindigkeit $f (2)$ eine Strecke von $1$ km zurücklegt.
  $f (2) = 120 \frac{km}{h} \Rightarrow s = \frac{1}{60} \cdot 120 \cdot t = 1 \Rightarrow t = \frac{1}{2}$
  Der gesamte Zeitraum, in dem genau $7$ km zurückgelegt werden, beträgt $2,5$ Minuten.
  Der Zeitraum beginnt um $15 : 00$ und endet $2,5$ Minuten später.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Geschwindigkeit von $15 : 00$ Uhr bis $15 : 02$ Uhr wird mithilfe der Funktion $f$ beschrieben. Berechne in diesen $2$ Minuten zurückgelegte Strecke dann durch das Integral: $s (2) = \frac{1}{60} \int_{0}^{2} f (x) d x$
  Da diese Strecke kleiner als 7 km ist, muss noch die Zeit berechnet werden, in der der ICE mit der konstanten Geschwindigkeit $f (2)$ die restliche Strecke zurücklegt.
6. Untersuchen Sie, ob folgende Aussage richtig ist: (6 BE)
  Wenn sich die Abnahme der Geschwindigkeit von 15: 01 Uhr an nicht mehr verändern würde, dann käme der ICE von diesem Zeitpunkt an nach drei Kilometern zum Stehen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
  Prüfung der Aussage
  Steigung um 15:01 Uhr
  Zum Zeitpunkt $15 : 01$ Uhr ist die Geschwindigkeit durch die Funktion $f (x) = 30 x^{3} - 90 x^{2} + 240$ gegeben.
  Gesucht ist nun die Gleichung der Tangente an den Graphen von $f$ im Punkt $(1 | 𝑓 (1))$ .
  Es ist $f^{'} (1) = - 90$ und $f (1) = 180$ . Dann folgt für die Tangentengleichung:
  $t (x) = - 90 \cdot x + b$ und mit $180 = - 90 \cdot 1 + b \Rightarrow b = 270$
  Dann ist $t (x) = - 90 \cdot x + 270$ .
  Die Tangente hat die Nullstelle $x = 3$ .
  Zurückgelegter Weg
  Für die zurückgelegte Strecke von $15 : 01$ Uhr bis $15 : 03$ Uhr ergibt sich:
  Der zurückgelegte Weg kann entweder mit der Formel für die Dreiecksfläche $\frac{1}{2} \cdot g \cdot h$ oder mithilfe eines Integrals berechnet werden.
  Berechnung mithilfe der Dreiecksfläche:
  $s = \frac{1}{2} \cdot \frac{2}{60} \cdot f (1) = \frac{1}{60} \cdot 180 = 3$
  Berechnung mithilfe eines Integrals:
  $s = \frac{1}{60} \cdot \int_{1}^{3} t (x) d x = 3$
  Die Aussage ist also richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Gleichung der Tangente an den Graphen von $f$ im Punkt $(1 | 𝑓 (1))$ .
  Berechne die Nullstelle der Tangente.
  Der zurückgelegte Weg kann entweder mit der Formel für die Dreiecksfläche $\frac{1}{2} \cdot g \cdot h$ oder mithilfe eines Integrals berechnet werden.
7. Betrachtet wird die in $ℝ$ definierte Funktion $s$ mit $s (x) = a \cdot \sin (b \cdot x) + c$ mit $a, b, c \in ℝ$ .
  Die Punkte $E_{1} (- 2 | - 1)$ und $E_{2} (2 | 3)$ sind direkt aufeinanderfolgende Extrempunkte des Graphen von $s$ .
  Bestimmen Sie die passenden Werte von $a, b$ und $c$ . (5 BE)
  [Zur Kontrolle: $a = 2, b = \frac{π}{4}, c = 1$ ]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion und Kosinusfunktion
  Passende Werte von $a, b$ und $c$
  Gegeben sind $s (x) = a \cdot \sin (b \cdot x) + c$ und $E_{1} (- 2 | - 1)$ und $E_{2} (2 | 3)$ .
  Die Ruhelage liegt in der Mitte zwischen Minimum und Maximum, also bei
  $y = \frac{1}{2} \cdot (3 + (- 1)) = 1$ . Der Parameter $c$ hat also den Wert $1$ .
  Die Amplitude ist die Differenz zwischen Maximum und der Ruhelage.
  Also ist der Parameter $a = 3 - 1 = 2$ .
  b ist der Periodenfaktor. Die Periode ist $p = \frac{2 \cdot π}{b}$ $\Rightarrow b = \frac{2 \cdot π}{p}$
  Der Abstand zwischen dem Minimum und dem Maximum entspricht einer halben Periode. $\Rightarrow \frac{p}{2} = | - 2 | + 2 = 4 \Rightarrow p = 8$
  Dann folgt für $b = \frac{2 \cdot π}{p} = \frac{2 \cdot π}{8} = \frac{π}{4}$
  Die passenden Werte sind $a = 2, b = \frac{π}{4}$ und $c = 1$ .
  Zur Veranschaulichung dient die folgende Abbildung.
  Sinusfunktion
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Ableitung von $s$ .
  An der Stelle $x = 2$ liegt ein Extremum vor, d.h. $s^{'} (2) = 0$ $\Rightarrow b$
  Setze die Koordinaten von $E_{1}$ und $E_{2}$ in $s$ ein.
  Du erhältst ein Gleichungssystem für die fehlenden Unbekannten $a$ und $c$ .
8. Berechnen Sie den Wert des Terms $\int_{- 2}^{2} s (x) d x$ . Beschreiben Sie mithilfe der Abbildung 2, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann. (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
  Wert des Terms $\int_{- 2}^{2} s (x) d x$
  Es ist $\int_{- 2}^{2} 2 \cdot \sin (\frac{π}{4} \cdot x) + 1 d x = 4$
  Beschreibung mithilfe der Abbildung 2, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann
  Die Funktion $s (x)$ ist wegen $c = 1$ punktsymmetrisch zum Punkt $(0 | 1)$ .
  Skizze
  Die beiden orangefarbigen Flächenstücke haben den gleichen Flächeninhalt $A_{1}$ bzw. $A_{4}$ . Ebenso haben die beiden grünen Flächenstücke den gleichen Flächeninhalt $A_{2}$ bzw. $A_{3}$ . Das gestreifte Quadrat hat den Flächeninhalt $4$ .
  Es ist also $A_{1} = A_{4}$ und $A_{2} = A_{3}$ .
  Für die Flächenbilanz gilt dann:
  $\int_{- 2}^{2} s (x) d x = - A_{1} + A_{2} + (4 - A_{3}) + A_{4} = - A_{1} + A_{2} + 4 - A_{2} + A_{1} = 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Funktion $s (x)$ ist wegen $c = 1$ punktsymmetrisch zum Punkt $(0 | 1)$ .
  Betrachte Flächenstücke, die den gleichen Flächeninhalt haben und bilde eine Flächenbilanz.
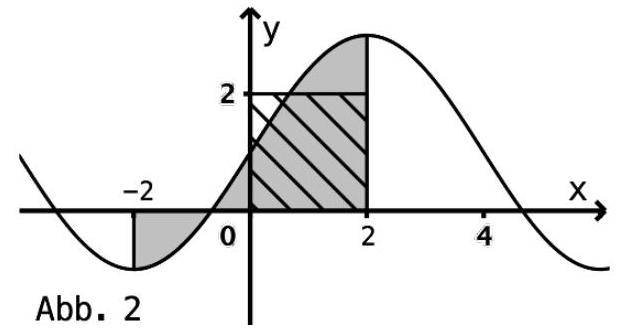
9. Die Punkte des Graphen von $s$ mit der $y$ -Koordinate 1 sind die Wendepunkte des Graphen. Die $x$ -Koordinate der Wendepunkte ist ganzzahlig und ein Vielfaches von 4. Die Steigung des Graphen von $s$ in jedem seiner Wendepunkte ist entweder $- \frac{π}{2}$ oder $+ \frac{π}{2}$ .
  Für jeden Wendepunkt des Graphen von $s$ wird die Gerade betrachtet, die durch diesen Wendepunkt und den Punkt $P (2022 | 2022)$ verläuft.
  Untersuchen Sie, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den
  Graphen von $s$ ist. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wichtige Zahlenmengen
  Untersuchung, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von $s$ ist
  Für die Wendepunkte gilt: $W P (4 k | 1)$ mit $k \in ℤ$ .
  Die Geraden verlaufen durch den Wendepunkt und den Punkt $P (2022 | 2022)$ .
  Für die Geradensteigungen gilt dann:
  $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{2022 - 1}{2022 - 4 k} = \frac{2021}{2022 - 4 k}$ mit $k \in ℤ$
  Die Steigung in den Wendepunkten ist entweder $- \frac{π}{2}$ oder $+ \frac{π}{2}$ , d.h. es handelt sich hier um irrationale Zahlen.
  Die Tangentensteigungen in den Wendepunkten sind $m = \frac{2021}{2022 - 4 k}$ .
  Der Wert von $m$ ist für jedes $k \in ℤ$ eine rationale Zahl.
  Das ist ein Widerspruch zu den Steigungen in den Wendepunkten.
  Keine der Geraden im jeweiligen Wendepunkt ist Tangente an den Graphen von $s$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Steigungen $m$ der Geraden, die durch die beiden Punkte $W P (4 k | 1)$ und $P (2022 | 2022)$ verlaufen.
  Vergleiche den Zahlenwert von $m$ mit den Zahlenwerten der Steigungen in den Wendepunkten bzgl. der Zugehörigkeit zu einer bestimmten Zahlenmenge.
4
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 2A
Ein Telefonanbieter bietet die Tarife S, M, und L an. Jeder Kunde hat genau einen dieser Tarife. Allen Kunden steht eine Service-Hotline zur Verfügung.
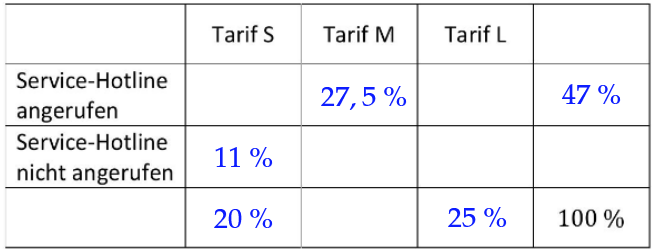
$20 %$ aller Kunden haben den Tarif S, $25 %$ den Tarif L. $47 %$ aller Kunden haben bereits die Service-Hotline angerufen. $27,5 %$ der Kunden haben den Tarif M und haben bereits die Service-Hotline angerufen.
$11 %$ haben den Tarif S und haben die Service-Hotline noch nicht angerufen.
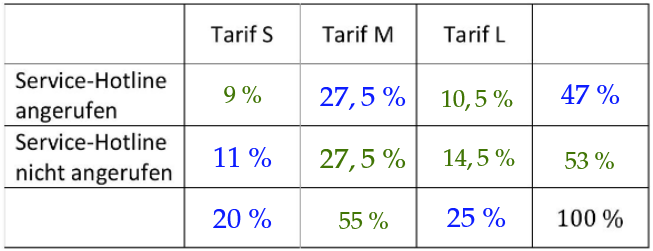
1. Stellen Sie alle Anteile - analog zu einer Vier-Felder-Tafel - in der folgenden Tabelle dar.
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
  Informationen aus der Aufgabenstellung
  Informationen aus der Aufgabenstellung
  Vollständige Tabelle
  Die restlichen Werte werden aus den einzelnen Zeilen und Spalten berechnet. Subtrahiere zum Beispiel für das Feld oben links: $20 % - 11 %$
  Vollständige Tabelle
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Übertrage die Daten aus der Aufgabenstellung in die "Vierfeldertafel".
  Ergänze die fehlenden Stellen. Achte darauf, dass die Summe innerhalb der Zeilen/Spalten immer dem Wert am Ende der Zeile/Spalte entsprechen müssen.
2. Ein zufällig ausgewählter Kunde hat die Service-Hotline noch nicht angerufen.
  Bestimmen Sie die Wahrscheinlichkeit dafür, dass dieser Kunde den Tarif S hat.
  (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
  Bedingte Wahrscheinlichkeit ermitteln
  Zur besseren Übersicht ist hier
  $S$ : Eine zufällig ausgewählte Person hat Tarif S
  $H$ : Eine zufällig ausgewählte Person hat bei der Servicehotline angerufen
  Durch die Formulierung in zwei Sätzen erkennst du, dass es sich um eine bedingte Wahrscheinlichkeit handelt. Dabei ist die Bedingung im ersten Satz: Es wurde keine Service Hotline angerufen ( $H$ ).
  Die gesuchte Wahrscheinlichkeit ist also:
  $P_{H} (S) = \frac{P (H \cap S)}{P (H)}$
  Wir entnehmen die Wahrscheinlichkeit aus der Tabelle in (a).
  $11 %$ aller Personen haben Tarif S und die Service-Hotline nicht angerufen.
  $53 %$ aller Personen haben die Service-Hotline nicht angerufen.
  Die Wahrscheinlichkeit, dass eine Person "Tarif S und die Service-Hotline nicht angerufen" hat, beträgt:
  $P_{H} (S) = \frac{P (H \cap S)}{P (H)} = \frac{11 %}{53 %} = 0,2075... \approx 20,75 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Anteil dieser Personengruppen. Hier kann auch die Formel für die bedingte Wahrscheinlichkeit helfen:
  Lese aus der Tabelle den Anteil der Kunden heraus, die noch nicht bei der Hotline angerufen haben und Tarif S haben.
  Lese aus der Tabelle den Anteil der Kunden heraus, die grundsätzlich noch nicht bei der Hotline angerufen haben.
3. Bestimmen Sie den Anteil aller Kunden, die entweder den Tarif $L$ haben oder die Service-Hotline noch nicht angerufen haben. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
  Berechnung des Anteils
  Aus der Tabelle in (a) entnehmen wir:
  $10,5 %$ haben den Tarif L, aber haben schon angerufen,
  $11 %$ haben angerufen, aber den Tarif S,
  $27,5 %$ haben angerufen, aber den Tarif M.
  Zusammen ergibt das: $10,5 % + 11 % + 27,5 % = 49 %$
  VorsichtFormulierung
  Die $14,5 %$ der Personen, die Tarif L und nicht angerufen haben, dürfen nicht mitberechnet werden. Diese entsprechen nicht dem Kriterium:
  "Entweder Tarif L oder nicht angerufen."
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Entnehme die korrekten Anteile der Tabelle.
  Achte darauf, dass Kunden, die den Tarif L haben und noch nicht angerufen haben, nicht mitberechnet werden dürfen. ("entweder...oder")
4. Der Anbieter führt eine Befragung unter 600 zufällig ausgewählten Kunden durch. Es kann davon ausgegangen werden, dass unter den Befragten die Anzahl derjenigen mit dem Tarif $S$ binomialverteilt ist.
  Beschreiben Sie die Bedeutung des folgenden Terms im Sachzusammenhang: (3 BE)
  $\sum_{k = 470}^{490} (\binom{600}{k}) \cdot {0,8}^{k} \cdot {0,2}^{600 - k}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Beschreibung des Terms
  Überlege dir, was die einzelnen Bestandteile des Terms bewirken:
  $80 %$ der befragten haben Tarif M oder Tarif L (siehe Tabelle (a)).
  Der Term ${0,8}^{k}$ berechnet also die Teilwahrscheinlichkeit, dass unter den 600 Befragten genau $k$ Personen Tarif L oder M haben.
  Umgekehrt gibt ${0,2}^{600 - k}$ das Gegenstück dazu an: Das ist die Teilwahrscheinlichkeit, dass die übrigen Befragten Tarif S haben.
  Insgesamt beschreibt der Term nur die Wahrscheinlichkeit eines möglichen Ergebnisses, bei dem genau k Personen nicht Tarif S haben.
  Der Binomialkoeffizient sorgt dann dafür, dass verschiedene Reihenfolgen berücksichtigt werden, um k Treffer zu erzielen.
  Das Summenzeichen $Σ$ bewirkt, dass die Wahrscheinlichkeiten für genau k Treffer im Bereich $470 \leq k \leq 490$ addiert werden. Dabei sind beide Grenzen mit in der Summe enthalten.
  Im Sachzusammenhang insgesamt: Der Term gibt die Wahrscheinlichkeit an, dass mindestens 470 und höchstens 490 der Befragten Tarif M oder L haben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Interpretiere die Wahrscheinlichkeiten. Welcher Anteil könnte $80 %$ betragen?
  Überlege dir die Bedeutung des Terms ${0,8}^{k} \cdot {0,2}^{600 - k}$ .
  Überlege dir, was der Binomialkoeffizient beiträgt.
  Überlege, was die Summe der Wahrscheinlichkeiten von $k = 470$ bis $k = 490$ bedeutet.
  Übertrage deine Erkenntnisse auf die Sachsituation
5. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Anzahl der Kunden mit dem Tarif S um höchstens $5 %$ vom Erwartungswert abweicht. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Erwartungswert
  Für die Binomialverteilung mit $n = 600$ und einer Wahrscheinlichkeit von $p = 0,2$ für Tarif S ist:
  $μ = n \cdot p = 600 \cdot 0,2 = 120$
  Bereich der Abweichung
  Weicht man $5 %$ von $μ = 120$ ab, beträgt das in Personen:
  $120 \cdot 0,05 = 6$
  Somit muss die Wahrscheinlichkeit im Bereich $\underset{120 - 6}{\underset{⏟}{114}} \leq X \leq \underset{120 + 6}{\underset{⏟}{126}}$ berechnet werden.
  Wahrscheinlichkeit für die Abweichung
  Gesucht ist die Wahrscheinlichkeit $P (114 \leq X \leq 126)$ .
  Mit dem Taschenrechner kann die Verteilungsfunktion (oft BinomialCDF) eingestellt werden. Hier lässt sich die Wahrscheinlichkeit berechnen durch:
  $P (114 \leq X \leq 126)$ $=$ $\underset{Taschenrechner}{\underset{⏟}{F_{600; 0,2} (k = 126) - F_{600; 0,2} (k = 113)}}$
  $\approx$ $0,7483 - 0,2554$
  $=$ $49,29 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Erwartungswert $μ$ für die Anzahl der Kunden mit Tarif S.
  Berechne, wie viel die Abweichung $5 %$ in Personen entspricht.
  Berechne die Wahrscheinlichkeit für den Bereich von $μ - 5 %$ bis $μ + 5 %$
6. Bestimmen Sie die größte natürliche Zahl $k$ , für die die Wahrscheinlichkeit dafür, dass unter den Befragten weniger als $k$ Kunden den Tarif $S$ haben, kleiner als $25 %$ ist. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Werte der Verteilungsfunktion
  Mit den Parametern $n = 600$ und $p = 0,2$ (für Tarif S) ergibt sich mit der Verteilungsfunktion auf dem Taschenrechner:
  $P (X < \underset{k}{\underset{⏟}{111}}) = P (X \leq 110) = F_{600; 0,2} (110) \approx 0,1662$
  $P (X < \underset{k}{\underset{⏟}{112}}) = P (X \leq 111) = F_{600; 0,2} (111) \approx 0,1935$
  $P (X < \underset{k}{\underset{⏟}{113}}) = P (X \leq 112) = F_{600; 0,2} (112) \approx 0,2232$ $\leftarrow$
  $P (X < \underset{k}{\underset{⏟}{114}}) = P (X \leq 113) = F_{600; 0,2} (113) \approx 0,2553$
  Der größtmögliche Wert für $k$ ist $k = 113$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Wahrscheinlichkeit mithilfe der Binomialverteilung bzw. Verteilungsfunktion.
  Auf dem Taschenrechner kann mit "BinomialCDF" die Verteilungsfunktion eingestellt werden.
  Probiere aus, für welchen Wert von $k$ eine Wahrscheinlichkeit kleiner $0,25$ herauskommt.
7. Die Wartezeit beim Anrufen der Service-Hotline ist normalverteilt mit einer Standardabweichung von 1 Minute und 15 Sekunden.
  Angenommen, die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Anrufer höchstens drei Minuten warten muss, beträgt $15 %$ .
  Berechnen Sie unter dieser Annahme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Anrufer mindestens fünf Minuten warten muss. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Erwartungswert der Normalverteilung
  Die Normalverteilung $φ$ hat die Parameter $μ$ und $σ$ .
  $μ$ muss aus einer Gleichung bestimmt werden
  $σ = 1,25 min$ aus der Aufgabenstellung
  Gegeben ist:
  $0,15$ $=$ $P (X \leq 3)$
  ↓
  Ist das Integral von $- \infty$ bis $3$
  $0,15$ $=$ $\int_{- \infty}^{3} φ_{μ; 1,25} (x) d x$
  ↓
  Bestimmt der Taschenrechner
  $μ$ $\approx$ $4,3$
  Wahrscheinlichkeit $P (X \geq 5)$
  Mit dem berechneten Erwartungswert erhalten wir:
  $P (X \geq 5) = \int_{5}^{\infty} φ_{4,3; 1,25} (x) d x \overset{Taschenrechner}{\approx} 29 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wir untersuchen jetzt $X$ die Länge der Wartezeit in Minuten.
  Bestimme mit $P (X \leq 3) = 15 %$ den Erwartungswert der Verteilung.
  Verwende diese Gleichung und den CAS, um das Integral numerisch ausrechnen zu lassen.
  Bestimme $P (X \geq 5)$ , wobei der berechnete Erwartungswert hier verwendet werden muss.
8. Untersuchen Sie, ob es ein Zeitintervall mit einer Länge von zwei Minuten gibt, in dem die Wartezeit eines zufällig ausgewählten Anrufers mit einer Wahrscheinlichkeit von mindestens $60 %$ liegt. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Überschlag
  Die größtmögliche Wahrscheinlichkeit befindet sich im Bereich um den Erwartungswert.
  Berechnet man $P (μ - 1 \leq X \leq μ + 1)$ müsste man den größtmöglichen Wert für die Wahrscheinlichkeit erhalten.
  Es gilt: $P (μ - 1 \leq X \leq μ + 1) \approx 57,6 % < 60 %$
  Selbst wenn man im Intervall mit der größtmöglichen Wahrscheinlichkeit sucht, liegt sie nicht über mindestens $60 %$ .
  $\Rightarrow$ Das gesuchte Intervall gibt es nicht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überschlage diese Rechnung, indem du das 2-minütige Intervall um den Erwartungswert betrachtest.
  Berechne die Wahrscheinlichkeit in diesem Intervall und interpretiere.

Aufgabe 2B

Unter den Kunden eines Krankenversicherungsunternehmens haben $59 %$ Datenschutzbedenken. Von den Kunden mit Datenschutzbedenken nutzen $23 %$ ein Fitnessarmband. $19 %$ aller Kunden haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.

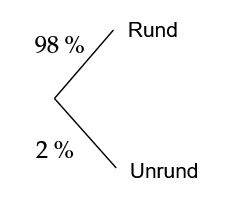
Stellen Sie den Sachverhalt in einem beschrifteten Baumdiagramm dar. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Vierfeldertafel
Knoten des Baumdiagramms
Die Merkmale in diesem Zufallsexperiment sind:
$D$ : Hat Datenschutzbedenken
$\overline{D}$ : Hat keine Datenschutzbedenken
$F$ : Hat ein Fitnessarmband
$\overline{F}$ : Hat kein Fitnessarmband
Jedes Ereignis musst du auf eine Stufe eingezeichnen. Dadurch ergibt sich ein 2-stufiges Baumdiagramm.
Der Satz "Von den Kunden mit Datenschutzbedenken nutzen $23 %$ ein Fitnessarmband." verrät uns, dass auf der ersten Stufe die Datenschutzbedenken stehen müssen.
Wahrscheinlichkeiten des Baumdiagramms
vollständiges Baumdiagramm
Die schwarzen Wahrscheinlichkeiten wurden aus der Aufgabenstellung übernommen
Die blauen Wahrscheinlichkeiten müssen berechnet werden
Die Summe der Wahrscheinlichkeiten, die von einem Knoten ausgehen, ist 100%
Die 1. Pfadregel kann genutzt werden, um beim 3. Pfad die fehlende Wahrscheinlichkeit zu bestimmen
VorgehenWahrscheinlichkeit unten rechts im Baumdiagramm
$19 %$ aller Kunden haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.
Diese Wahrscheinlichkeit kann nicht direkt in das Innere des Baumdiagramms übernommen werden.
Man berechnet:
$\underset{Hat keine Datenschutzbedenken}{\underset{⏟}{0,41}} \cdot \underset{Hat ein Fitnessarmband}{\underset{⏟}{x}} = 0,19$
$\Rightarrow x \approx 46,34 %$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die zwei Merkmale, die hier untersucht werden.
Skizziere für jedes Merkmal eine Stufe und trage die Wahrscheinlichkeiten ein.
Achte dabei auf die Reihenfolge: Gibt es bei einer Wahrscheinlichkeit eine Vorbedingung, sollte das Merkmal auf die zweite Stufe
Bestimme mit den Pfadregeln die übrigen Wahrscheinlichkeiten.
Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband. Bestimmen Sie die Wahrscheinlichkeit dafür, dass sie Datenschutzbedenken hat.
(3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Da die Aufgabenstellung in zwei Sätzen formuliert ist, handelt es sich um die bedingte Wahrschienlichkeit $P_{F} (D)$ .
Person benutzt ein Fitnessarmband
Im Baumdiagramm können die Wahrscheinlichkeiten aller Pfade entnommen werden, in dem das Ereignis $F$ (steht für "Person hat Fitnessarmband") zutrifft. Es werden die Pfadregeln verwendet.
$P (F) = 0,59 \cdot 0,23 + 0,41 \cdot 0,4634 \approx 0,3257$
Bedingte Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit, dass $D$ eintrifft (Datenschutzbedenken) unter der Bedingung $F$ (Fitnessarmband), ist:
$P_{F} (D)$ $=$ $\frac{P (D \cap F)}{P (F)}$
↓
$P (F)$ von oben
$=$ $\frac{P (D \cap F)}{0,3257}$
↓
Baumdiagramm
$=$ $\frac{0,59 \cdot 0,23}{0,3257}$
$\approx$ $0,4166$
Die Wahrscheinlichkeit beträgt etwa $41,66 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme mit den Pfadregeln die Wahrscheinlichkeit, dass eine Person ein Fitnessarmband benutzt
Berechne die gesuchte Wahrscheinlichkeit mit der Formel für die bedingte Wahrscheinlichkeit:
$P_{B} (A) = \frac{P (A \cap B)}{P (B)}$
Es gilt $0,23 \neq 0,59 \cdot 0,23 + 0,19$ .
Begründen Sie damit, dass die Ereignisse „Eine unter allen Kunden zufällig ausgewählte Person hat Datenschutzbedenken.“ und „Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband." stochastisch abhängig sind. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
Bedeutung der Terme
Die linke Seite beschreibt gerade die Wahrscheinlichkeit (siehe Baumdiagramm):
$P_{D} (F)$
Die rechte Seite entspricht der Wahrscheinlichkeit (siehe (b)):
$P (F)$
Wenn die Terme ungleich sind, gilt entsprechend: $P_{D} (F) \neq P (F)$ .
Das heißt, dass der Ausgang von $F$ von der Bedingung $D$ abhängt. Sie sind stochastisch abhängige Ereignisse.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Untersuche die Terme und deren Bedeutung im Sachzusammenhang. Welche Ereignisse stellen sie dar?
Das Kriterium für stochastische Unabhängigkeit für Ereignisse $A$ und $B$ ist:
$P (A \cap B) = P (A) \cdot P (B)$ oder äquivalent $P (A | B) = P (A)$
100 Kunden des Unternehmens werden zufällig ausgewählt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass mehr als $50 %$ der ausgewählten Kunden Datenschutzbedenken haben. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Das Zufallsexperiment
Laut Baumdiagramm haben $59 %$ aller Personen Datenschutzbedenken. Damit ist $p = 0,59$ der Parameter des Zufallsexperiments.
Wir gehen davon aus, dass diese Wahrscheinlichkeit für das Auswählen jeder einzelnen Person gilt, womit die Anzahl der Kunden mit Datenschutzbedenken $X$ binomialverteilt wäre.
$n = 100$ ist die Länge unserer Bernoulli-Kette. Mehr als $50 %$ der Kunden soll Datenschutzbedenken haben, also $k > 50$ .
Wahrscheinlichkeit $P (X > 50)$
Für die Binomialverteilung mit Parametern $n = 100, p = 0,59$ gilt:
Verwenden des Gegenereignis
↓
$P (X > 50)$ $=$ $1 - P (X \leq 50)$
↓
Verwenden der Verteilungsfunktion
$=$ $1 - F_{100; 0,59} (50)$
↓
Taschenrechner
$=$ $1 - 0,0427...$
$\approx$ $95,72 %$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Zufallsvariable $X$ , welche die Kunden mit Datenschutzbedenken zählt, ist binomialverteilt.
Bestimme die Wahrscheinlichkeit $P (X > 50)$ mit der Binomialverteilung.
Setzt man für $a$ und $b$ geeignete Werte ein, so kann mit dem Term
$1 - \sum_{k = 51}^{100} (\binom{100}{k}) \cdot {0,59}^{k} \cdot a^{b}$
die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden.
Geben Sie diese Werte für $a$ und $b$ an.
Beschreiben Sie das zugehörige Ereignis. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Beschreibung des Ereignisses
Aus Teilaufgabe (d) oder aus dem Baumdiagramm ist das Ereignis: "Kunde hat Datenschutzbedenken" ( $D$ ) bekannt. Für dieses Ereignis gilt: $P (D) = 0,59$
Die Summe von $k = 51$ bis $k = 100$ beschreibt die Wahrscheinlichkeit, dass mindestens $51$ Kunden Datenschutzbedenken haben. $P (X \geq 51)$
Das Subtrahieren der Summe von $1$ weist darauf hin, dass hier ein Gegenereignis berechnet wird: $\underset{Gegenereignis}{\underset{⏟}{1 -}} \underset{P (X \geq 51)}{\underset{⏟}{\sum_{k = 51}^{100} (\binom{100}{k}) \cdot {0,59}^{k} \cdot a^{b}}}$
Insgesamt ist also $P (X \leq 50)$ gesucht - die Wahrscheinlichkeit des Ereignisses "Höchstens 50 der Kunden haben Datenschutzbedenken".

Werte für $a$ und $b$
a ist die Gegenwahrscheinlichkeit von 0,59. Es gilt: $a + 0,59 = 1 \Leftrightarrow a = 0,41$
$k$ und $b$ ergeben zusammen $100$ : $b = 100 - k$
Eingesetzt wäre der Term: $1 - \sum_{k = 51}^{100} (\binom{100}{k}) \cdot {0,59}^{k} \cdot {0,41}^{100 - k}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme ein Ereignis, welches die Trefferwahrscheinlichkeit $p = 0,59$ hat.
Verwende hierzu Teilaufgabe (d).
$a$ und $0,59$ müssen zusammenaddiert $1$ ergeben.
$b$ und $k$ müssen zusammen $100$ ergeben.
Untersuchen Sie, ob es eine natürliche Zahl $n$ gibt, für die die folgende Aussage richtig ist:
Werden $2 n$ Kunden des Unternehmens zufällig ausgewählt, so ist die Wahrscheinlichkeit dafür, dass unter diesen niemand Datenschutzbedenken hat, halb so groß wie bei $n$ Kunden.
(3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Terme der Wahrscheinlichkeiten
Die Wahrscheinlichkeit von "Niemand der $2 n$ Kunden hat Datenschutzbedenken" ist gegeben durch die Binomialverteilung:
$P_{2 n} (X = 0)$ $=$ $(\binom{2 n}{0}) \cdot {0,59}^{0} \cdot {0,41}^{2 n - 0}$
↓
Binomialkoeffizient ist 1. Außerdem ${0,59}^{0} = 1$
$=$ $1 \cdot 1 \cdot {0,41}^{2 n}$
$=$ ${0,41}^{2 n}$
Gleichermaßen ist die Wahrscheinlichkeit im Fall von $n$ Personen:
$P_{n} (X = 0)$ $=$ $(\binom{2 n}{0}) \cdot {0,59}^{0} \cdot {0,41}^{n - 0}$
↓
Binomialkoeffizient ist 1. Außerdem ${0,59}^{0} = 1$
$=$ $1 \cdot 1 \cdot {0,41}^{n}$
$=$ ${0,41}^{n}$
Gleichung untersuchen
Die Wahrscheinlichkeit für $2 n$ Personen soll halb so groß sein:
${0,41}^{2 n} \cdot 2 = {0,41}^{n}$
${0,41}^{2 n} \cdot 2$ $=$ ${0,41}^{n}$ $: {0,41}^{n}$
$\frac{{0,41}^{2 n}}{{0,41}^{n}} \cdot 2$ $=$ $1$
↓
Potengesetze
${0,41}^{n} \cdot 2$ $=$ $1$ $: 2$
${0,41}^{n}$ $=$ $\frac{1}{2}$
Wenn $0,41$ mit sich selbst multipliziert wird, wird das Produkt immer kleiner.
Das Produkt kann daher nie $0,5$ ergeben, sodass die gesuchte Zahl $n$ nicht existieren kann.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle die Wahrscheinlichkeit für "Niemand hat Datenschutzbedenken" als Term dar. Setze die Gesamtzahl der Personen hier $2 n$ .
Stelle die gleiche Wahrscheinlichkeit für "Niemand hat Datenschutzbedenken" dar, wobei die Gesamtzahl der Personen im zweiten Fall $n$ ist.
Setze $P_{2 n} (X = 0) \cdot \frac{1}{2} = P_{n} (X = 0)$ und stelle die Gleichung um. Interpretiere das Ergebnis.

Bevor Fitnessarmbänder in den Verkauf gelangen, wird ihre Funktionsfähigkeit überprüft.

Erfahrungsgemäß sind $10 %$ der Fitnessarmbänder falsch eingestellt.

Berechnen Sie, wie viele Fitnessarmbänder mindestens überprüft werden müssen, um mit einer Wahrscheinlichkeit von mindestens $99 %$ mindestens ein falsch eingestelltes Fitnessarmband zu entdecken. (3 BE)

An 5 Kontrollstationen werden jeweils 10 Fitnessarmbänder kontrolliert. Bestimmen Sie die Wahrscheinlichkeit dafür, dass höchstens an einer Kontrollstation mindestens ein falsch eingestelltes Fitnessarmband entdeckt wird. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Wahrscheinlichkeit $P (X \leq 1)$
Die Anzahl der defekten Armbänder $X$ ist binomialverteilt mit den Parametern $n = 10$ , $p = 0,1$ und $k \geq 1$ .
Gegenereignis
↓
$P (X \geq 1)$ $=$ $1 - P (X = 0)$
↓
Binomialverteilung
$\approx$ $1 - 0,3487$
$=$ $0,6513$
Wahrscheinlichkeit für defekte Armbänder an höchstens einer Kontrollstation
Die Wahrscheinlichkeit für mindestens ein defektes Armband wird hier als Parameter $p$ verwendet.
Es werden $n = 5$ Kontrollstationen untersucht und die Anzahl der Kontrollstationen mit defekten Armbändern " $Z$ " soll höchstens $1$ sein:
Verteilungsfunktion
↓
$P (Z \leq 1)$ $=$ $F_{5; 0,6513} (1)$
↓
Taschenrechner
$\approx$ $0,0533$
Die Wahrscheinlichkeit beträgt etwa $5,3 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Wahrscheinlichkeit, dass unter $10$ Fitnessarmbändern mindestens eines defekt ist: $P (X \geq 1)$ .
Diese Wahrscheinlichkeit ist als Parameter $p$ für das nächste Zufallsexperiment zu betrachten.
Berechne die Wahrscheinlichkeit, dass "mindestens ein Defekt" an höchstens einer Kontrollstation gefunden wird. Diese ist auch binomialverteilt.

6
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 2C
Ein Unternehmen stellt Tischtennisbälle her. $98 %$ der hergestellten Bälle weichen nur unwesentlich von der Kugelform ab; diese werden im Weiteren als „rund“ bezeichnet, die übrigen als „unrund“. Aus der großen Menge der hergestellten Bälle werden regelmäßig Stichproben entnommen, wobei die Auswahl der Bälle für jede Stichprobe als zufällig angenommen werden kann. Außerdem kann davon ausgegangen werden, dass die Anzahl der unrunden Bälle in jeder Stichprobe binomialverteilt ist.
1. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Anzahl unrunder Bälle in einer Stichprobe von 200 Bällen kleiner als der Erwartungswert dieser Anzahl ist. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Erwartungswert der Stichprobe
  Die Anzahl der unrunden Bälle wird mit $X$ bezeichnet. $X$ ist laut Angabe binomialverteilt. Für den Erwartungswert gilt:
  $μ$ $=$ $n \cdot p$
  ↓
  $n = 200, p = 0,02$ ( $2 %$ der Bälle sind unrund)
  $=$ $200 \cdot 0,02$
  $=$ $4$
  Wahrscheinlichkeit $P (X < 4)$
  $X$ ist binomialverteilt mit den Parametern $n = 200$ und $p = 0,02$ .
  Umformuliert
  ↓
  $P (X < 4)$ $=$ $P (X \leq 3)$
  ↓
  Verteilungsfunktion
  $=$ $F_{200; 0,02} (3)$
  ↓
  Taschenrechner (BinomialCDF)
  $\approx$ $0,4315$
  Die Wahrscheinlichkeit $P (X < 4)$ beträgt $43,15 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den erwarteten Wert für die Stichprobe $n = 200$ .
  Berechne die Wahrscheinlichkeit $P (X < μ)$ . Achte darauf, dass die Wahrscheinlichkeit binomialverteilt ist.
2. Betrachtet werden zwei Stichproben von jeweils 200 Bällen. Berechnen Sie die Wahrscheinlichkeit dafür, dass in mindestens einer dieser beiden Stichproben mehr als sechs Bälle unrund sind. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Wahrscheinlichkeit $P (X > 6)$
  Wie in Teilaufgabe (a) ist $X$ binomialverteilt. Es gilt:
  Verwende das Gegenereignis
  ↓
  $P (X > 6)$ $=$ $1 - P (X \leq 6)$
  ↓
  Verteilungsfunktion der Binomialverteilung
  $=$ $1 - F_{200; 0,02} (6)$
  ↓
  Taschenrechner (BinomialCDF)
  $\approx$ $1 - 0,8914$
  $\approx$ $0,1086$
  Wahrscheinlichkeit für die Stichproben
  Es gibt drei verschiedene Möglichkeiten, wie in mindestens einer dieser beiden Stichproben mehr als sechs Bälle unrund sind:
  In der 1. Stichprobe sind mehr als 6 Bälle unrund.
  In der 2. Stichprobe sind mehr als 6 Bälle unrund.
  In beiden Stichproben sind mehr als 6 Bälle unrund.
  Mit dem Gegenereignis "In beiden Stichproben sind weniger als 6 Bälle unrund." ergibt sich:
  $1 - {(P (X \leq 6))}^{2}$
  ↓
  Einsetzen der Wahrscheinlichkeit
  $=$ $1 - {0,8914}^{2}$
  $\approx$ $0,2054$
  Die Wahrscheinlichkeit beträgt etwa $20,54 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Wahrscheinlichkeit $P (X > 6)$ (mehr als 6 Bälle sind unrund).
  Berechne die Wahrscheinlichkeit für die beiden Stichproben.
  Das Gegenereignis kann die Rechnung deutlich vereinfachen.
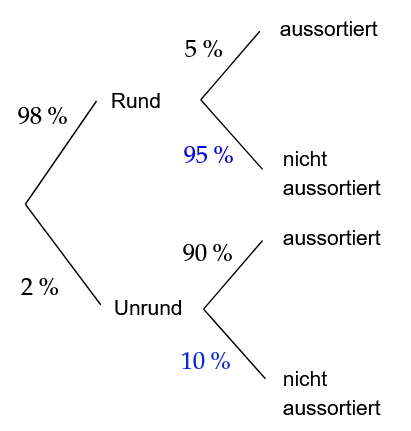
3. Nach der Herstellung durchlaufen die Bälle eine Sortieranlage. Dabei wird ein unrunder Ball mit einer Wahrscheinlichkeit von $90 %$ aussortiert. Allerdings werden auch $5 %$ der runden Bälle aussortiert.
  Stellen Sie den Prozess der Herstellung und Sortierung der Bälle in einem beschrifteten Baumdiagramm dar. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Erste Stufe
  Aus der Aufgabenstellung lassen sich die Wahrscheinlichkeiten der Ereignisse ablesen:
  $98 %$ der Bälle sind rund
  $2 %$ der Bälle sind unrund
  Erste Stufe des Baumdiagramms
  Zweite Stufe
  In der zweiten Stufe werden die Ereignisse "aussortiert" und "nicht aussortiert" dargestellt.
  Runde Bälle werden in $5 %$ der Fälle aussortiert.
  Unrunde Bälle werden in $90 %$ der Fälle aussortiert.
  Die blauen Wahrscheinlichkeiten lassen sich berechnen.
  Die Wahrscheinlichkeiten der Ereignisse, die aus einem "Knoten" im Baumdiagramm kommen, ergeben zusammen immer $100 %$ .
  Vollständiges Baumdiagramm
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere die erste Stufe des Baumdiagramms mit den Ereignissen "rund" und "unrund".
  Skizziere die zweite Stufe des Baumdiagramms mit den Angaben der Teilaufgabe (c).
4. Beschreiben Sie die Bedeutung des Terms $0,98 \cdot 0,05 \cdot 2000$ im Sachzusammenhang.
  (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
  Bedeutung des Terms
  Die Faktoren $0,98 \cdot 0,05$ beschreiben die Wahrscheinlichkeit eines runden, aussortierten Balls.
  Multipliziert man die Wahrscheinlichkeit mit einer Anzahl wie 2000, ergibt sie die zu erwartende Anzahl von runden, aussortierten Bällen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Untersuche die Faktoren und vergleiche mit den Wahrscheinlichkeiten aus den Teilaufgaben davor.
  Stichwort: Erwartungswert
5. Angenommen, die nicht aussortierten Bälle würden die gleiche Sortieranlage ein zweites Mal durchlaufen.
  Ermitteln Sie den Anteil der unrunden Bälle unter denjenigen, die dann nach zweimaligem Durchlaufen der Anlage nicht aussortiert würden. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
  Relativer Anteil
  Wir untersuchen den Anteil der unrunden Bälle, die nach dem zweiten Durchlauf nicht aussortiert wurden, von den Bällen, die nach zwei Durchläufen nicht aussortiert wurden.
  $\frac{P (unrund, zwei mal nicht aussortiert)}{P (aussortiert)}$
  ↓
  Baumdiagramm
  $=$ $\frac{0,02 \cdot 0,1 \cdot 0,1}{0,98 \cdot 0,95 \cdot 0,95 + 0,02 \cdot 0,1 \cdot 0,1}$
  $\approx$ $0,00023$
  Der Anteil beträgt etwa $0,023 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Wahrscheinlichkeit, dass ein unrunder Ball zweimal nicht aussortiert wird.
  Berechne die Wahrscheinlichkeit, dass irgendein Ball zweimal nicht aussortiert wird.
  Bilde das Verhältnis der beiden Werte.
6. Das Gewicht eines Tischtennisballs soll 2,70 Gramm (g) betragen. Das Gewicht der Bälle in der Produktion wird als normalverteilt angenommen mit $μ = 2,70$ und $σ = 0,03$ . Bei der Qualitätskontrolle von Tischtennisbällen in der Produktion werden jeweils 24 Bälle getestet. Es gelten folgende Regeln:
  I) Jedes Gewicht zwischen 2,67 $g$ und 2,77 $g$ ist akzeptabel, wobei einer der getesteten Bälle ein Gewicht außerhalb dieses Toleranzbereichs aufweisen darf.
  II) Keiner der Bälle darf ein Gewicht von unter 2,60 g oder über 2,85 g aufweisen.
  Bei der Qualitätskontrolle der Bälle gibt es Bereiche von Gewichten, in denen nach den Regeln I und II das Gewicht höchstens eines der Bälle liegen darf, ohne dass es zu einer Beanstandung bei der Kontrolle kommt.
  Bestimmen Sie die Wahrscheinlichkeit dafür, dass das Gewicht eines zufällig ausgewählten Balles der Produktion innerhalb dieser Bereiche von Gewichten liegt.
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Wahrscheinlichkeit berechnen
  Ein Gewicht zwischen $2,67$ g und $2,77$ g ist nicht zu beanstanden. Ein Ball darf mit seinem Gewicht außerhalb dieses Bereiches liegen, also in:
  $[2,6; 2,67] oder [2,77; 2,85]$
  Mit dem Taschenrechner und der Normalverteilung mit den Parametern $μ = 2,70, σ = 0,03$ gilt:
  $P ($ $2,6 \leq X \leq 2,67) = 0,1582$
  $P (2,77 \leq X \leq 2,85) = 0,0098$
  Dabei steht $X$ für das normalverteilte Gewicht des Balls. Zusammen ist die Wahrscheinlichkeit:
  $P (2,6 \leq X \leq 2,67) + (2,77 \leq X \leq 2,85) = 0,1680 = 16,8 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Verwende die Normalverteilung mit den Parametern $μ = 2,70$ und $σ = 0,03$ .
  Bestimme die Wahrscheinlichkeit mit dem TR, dass das Gewicht des Balls in den Bereichen $[2,6; 2,67]$ oder $[2,77; 2,85]$ liegt.
7. Bestimmen Sie die Wahrscheinlichkeit dafür, dass bei einer Qualitätskontrolle von 24 Bällen keine Beanstandung aufgrund von Regel I auftritt. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Wahrscheinlichkeit, dass das Gewicht in $[2,67; 2,77]$ liegt
  Mit der Normalverteilung und den Parametern $μ = 2,70, σ = 0,03$ gilt:
  $P (2,67 \leq X \leq 2,77) = 0,8315$
  Von den 24 Bällen darf ein Ball von seinem etwas Gewicht abweichen.
  Die Wahrscheinlichkeit, dass dieser Ball im Bereich $[2,6; 2,85]$ liegt, ist:
  $P (2,6 \leq X \leq 2,85) = 0,9996$
  Insgesamt ist:
  $P (Regel I erfüllt)$
  ↓
  Teilaufgabe (g)
  $=$ $\underset{Alle Bälle in [2,67;2,77]}{\underset{⏟}{{0,8315}^{24}}} + \underset{Ein Ball in [2,60;2,67] \cup [2,77; 2,85]}{\underset{⏟}{{0,8315}^{23} \cdot 0,1680 \cdot 24}}$
  $=$ $0,07$
  Die Wahrscheinlichkeit beträgt 7 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Von 24 Bällen darf ein Ball vom Gewicht abweichen.
  Berechne die Wahrscheinlichkeit, dass 24 Bälle Regel I erfüllen.
  Berechne die Wahrscheinlichkeit, dass 23 Bälle die Regel I erfüllen und ein Ball außerhalb des Bereichs $[2,67; 2,77]$ liegt. Verwende dabei die Binomialverteilung.
8. Durch Einstellung der Produktionsmaschine kann der Wert für $μ$ verändert werden. Der Wert von $σ$ bleibt dabei unverändert.
  Entscheiden Sie, ob $μ = 2,70$ die optimale Einstellung der Maschine ist und begründen Sie Ihre Entscheidung. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Entscheidung und Begründung
  Nein, die Einstellung ist nicht optimal.
  Das Gewicht der "meisten" Bälle liegt um den Erwartungswert verteilt. Darum sollte dieser mittig im Intervall $[2,67; 2,77]$ liegen: $\Rightarrow μ = 2,72$
  Damit wäre die Wahrscheinlichkeit maximiert, dass das Gewicht der Bälle in $[2,67; 2,77]$ liegt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Untersuche die Normalverteilung und den Erwartungswert.
  Wo müsste dieser im optimalen Fall liegen, so dass die Wahrscheinlichkeit für den Bereich $[2,67; 2,77]$ maximal ist?
7
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 3A
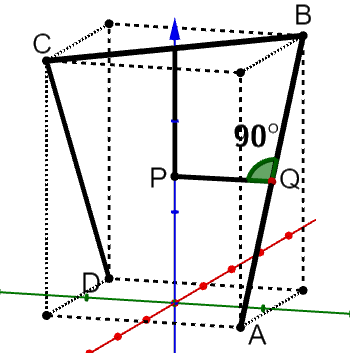
Die Abbildung zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland. Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken $A B, B C$ und $C D$ mit
$A (11 | 11 | 0), B (- 11 | 11 | 28), C (11 | - 11 | 28)$ und $D (- 11 | - 11 | 0)$ besteht. $A, B, C$ und $D$ sind Eckpunkte eines Quaders.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
1. Begründen Sie, dass die Punkte $B$ und $C$ symmetrisch bezüglich der $x_{3}$ -Achse liegen. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
  Begründung, dass die Punkte $B$ und $C$ symmetrisch bezüglich der $x_{3}$ -Achse liegen
  Sowohl die $x_{1}$ -Koordinaten als auch die $x_{2}$ -Koordinaten der beiden Punkte $B$ und $C$ unterscheiden sich nur in ihren Vorzeichen. Die $x_{3}$ -Koordinaten stimmen überein. Daher liegen die beiden Punkte $B$ und $C$ symmetrisch bezüglich der $x_{3}$ -Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die $x_{1}$ und $x_{2}$ -Koordinaten der Punkte $B$ und C, sowie die $x_{3}$ -Koordinaten dieser Punkte.
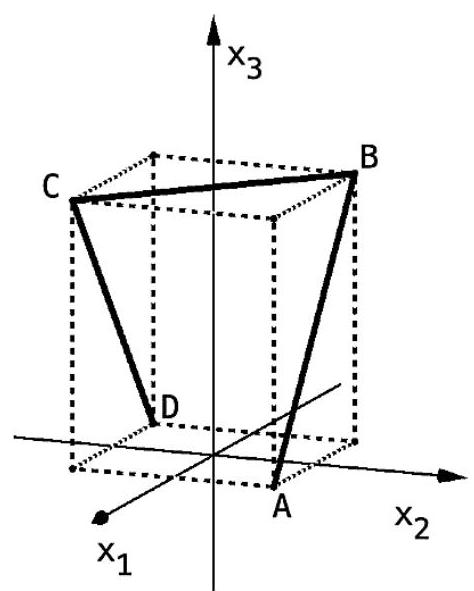
2. Berechnen Sie die Länge des Streckenzugs in der Wirklichkeit. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
  Länge des Streckenzugs in der Wirklichkeit
  Der Streckenzug setzt sich aus den Längen der drei Vektoren $\vec{A B}$ , $\vec{B C}$ und $\vec{C D}$ zusammen. Man berechnet die Vektoren und ihre Beträge.
  $\vec{A B} = \vec{O B} - \vec{O A} = (\begin{array}{c} - 11 \\ 11 \\ 28 \end{array}) - (\begin{array}{c} 11 \\ 11 \\ 0 \end{array}) = (\begin{array}{c} - 22 \\ 0 \\ 28 \end{array})$
  $| \vec{A B} | = \sqrt{(- 22)^{2} + 0^{2} + 28^{2}} = \sqrt{1268}$
  Aus Abbildung $2$ ist zu erkennen, dass der Betrag des Vektors $\vec{C D}$ gleich dem Betrag des Vektors $\vec{A B}$ ist. (Der Vektor $\vec{C D}$ muss nicht extra berechnet werden.)
  $\vec{B C} = \vec{O C} - \vec{O B} = (\begin{array}{c} 11 \\ - 11 \\ 28 \end{array}) - (\begin{array}{c} - 11 \\ 11 \\ 28 \end{array}) = (\begin{array}{c} 22 \\ - 22 \\ 0 \end{array})$
  $| \vec{B C} | = \sqrt{22^{2} + (- 22)^{2} + 0^{2}} = \sqrt{968}$
  Der Streckenzug setzt sich aus den Längen $2 \cdot | \vec{A B} | + | \vec{B C} | = 2 \cdot \sqrt{1268} + \sqrt{968}$ zusammen. Er hat etwa die Länge $102,33 m$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Streckenzug setzt sich aus den Längen $2 \cdot | \vec{A B} | + | \vec{B C} |$ .
  Berechne die beiden Vektoren und ihre Beträge.
3. Die Ebene $E$ enthält die Punkte $A, B$ und $C$ , die Ebene $F$ enthält die Punkte $B, C$ und $D$ .
  Bestimmen Sie eine Gleichung von $E$ in Koordinatenform. (3 BE)
  [Zur Kontrolle: $14 x_{1} + 14 x_{2} + 11 x_{3} = 308$ ]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalenvektor
  Gleichung von $E$ in Koordinatenform
  Die Vektoren $\vec{O A} = (\begin{array}{c} 11 \\ 11 \\ 0 \end{array})$ und $\vec{A B} = (\begin{array}{c} - 22 \\ 0 \\ 28 \end{array})$ sind schon bekannt (Aufgabe $a$ )). Der Vektor $\vec{A C}$ muss noch berechnet werden.
  $\vec{A C} = \vec{O C} - \vec{O A} = (\begin{array}{c} 11 \\ - 11 \\ 28 \end{array}) - (\begin{array}{c} 11 \\ 11 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ - 22 \\ 28 \end{array})$
  Dann gilt: ${\vec{n}}_{E} \circ \vec{A B} = 0$ und ${\vec{n}}_{E} \circ \vec{A C} = 0$
  Man erhält zwei Gleichungen:
  $(I) : - 22 \cdot n_{1} + 0 \cdot n_{2} + 28 \cdot n_{3} = 0$
  $(I I) : 0 \cdot n_{1} - 22 \cdot n_{2} + 28 \cdot n_{3} = 0$
  Rechne $(I) - (I I)$ :
  $- 22 \cdot n_{1} + 22 \cdot n_{2} = 0 \Rightarrow n_{1} = n_{2}$
  Wähle z.B.: $n_{1} = n_{2} = 14 \Rightarrow - 22 \cdot 14 + 28 \cdot n_{3} = 0 \Rightarrow n_{3} = \frac{22 \cdot 14}{28} = 11$
  Der Normalenvektor der Ebene $E$ ist ${\vec{n}}_{E} = (\begin{array}{c} 14 \\ 14 \\ 11 \end{array})$ .
  Die Ebenengleichung hat dann die Form $E : 14 x_{1} + 14 x_{2} + 11 x_{3} = d$
  Der Punkt $A (11 | 11 | 0)$ liegt dann in der Ebene, wenn $14 \cdot 11 + 14 \cdot 11 + 11 \cdot 0 = d$ ist. $\Rightarrow d = 308$
  Die Gleichung von $E$ in Koordinatenform lautet $14 x_{1} + 14 x_{2} + 11 x_{3} = 308$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: ${\vec{n}}_{E} \circ \vec{A B} = 0$ und ${\vec{n}}_{E} \circ \vec{A C} = 0$
  Löse das Gleichungssystem für ${\vec{n}}_{E}$ .
  Die Ebenengleichung hat dann die Form $E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = d$ .
  Der Punkt $A$ erfüllt die Ebenengleichung: $\Rightarrow d$
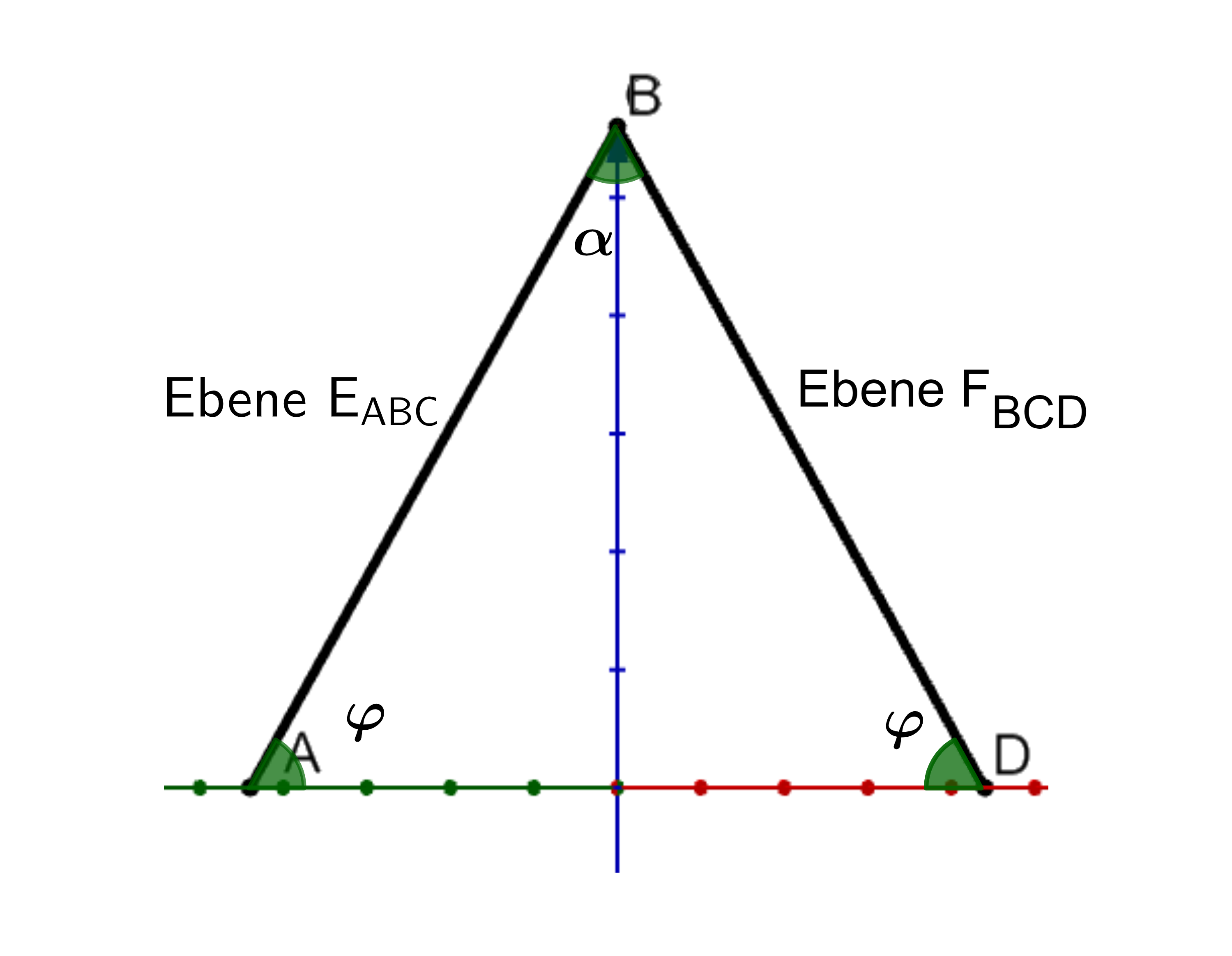
4. Berechnen Sie die Größe $α$ des Winkels, unter dem $E$ die $x_{1} x_{2}$ -Ebene schneidet.
  Geben Sie einen Term an, mit dem aus $α$ die Größe des Winkels zwischen den Ebenen $E$ und $F$ berechnet werden kann. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie
  Größe $α$ des Winkels, unter dem $E$ die $x_{1} x_{2}$ -Ebene schneidet
  Für den Schnittwinkel zweier Ebenen gilt: $𝐜 𝐨 𝐬 𝛂 = \frac{| \vec{𝐧} \circ \vec{𝐦} |}{| \vec{𝐧} | \cdot | \vec{𝐦} |}$
  Dabei sind $\vec{n}$ und $\vec{m}$ die Normalenvektoren der beiden Ebenen.
  Die Ebene $E$ hat den Normalenvektor $\vec{n} = (\begin{array}{c} 14 \\ 14 \\ 11 \end{array})$ und $| \vec{n} | = \sqrt{14^{2} + 14^{2} + 11^{2}} = \sqrt{513}$ .
  Die $x_{1} x_{2}$ -Ebene hat den Normalenvektor $\vec{m} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ und $| \vec{m} | = 1$ .
  $\cos (φ) x$ $=$ $\frac{| \vec{𝐧} \circ \vec{𝐦} |}{| \vec{𝐧} | \cdot | \vec{𝐦} |}$
  ↓
  Setze die Werte für die Vektoren und ihre Beträge ein.
  $=$ $\frac{| (\begin{array}{c} 14 \\ 14 \\ 11 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) |}{\sqrt{513} \cdot 1}$
  ↓
  Berechne das Skalarprodukt.
  $=$ $\frac{| 0 + 0 + 11 |}{\sqrt{513}}$
  $=$ $\frac{11}{\sqrt{513}}$
  Du hast die Gleichung $\cos (φ) = \frac{11}{\sqrt{513}}$ erhalten. Durch Anwendung der Umkehrfunktion des Kosinus kann der Winkel $φ$ berechnet werden. Man benutzt auf dem TR die Funktion $\cos^{- 1} (x)$ .
  $φ = \arccos (\frac{11}{\sqrt{513}}) \approx {60,94}^{\circ}$
  Der Schnittwinkel $φ$ , unter dem $E$ die $x_{1} x_{2}$ -Ebene schneidet, beträgt rund $61^{\circ}$ .
  Geben Sie einen Term an, mit dem aus $α$ die Größe des Winkels zwischen den Ebenen $E$ und $F$ berechnet werden kann
  Die folgende Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur der Veranschaulichung.
  Eingezeichnet sind die beiden Ebenen $E$ ( $orange$ ) und $F$ ( $grün$ ). Der Schnittwinkel, unter dem $E$ die $x_{1} x_{2}$ -Ebene schneidet, ist der Winkel $φ$ . Aus Symmetriegründen schneidet die Ebene $F$ die $x_{1} x_{2}$ -Ebene unter dem gleichen Winkel $φ$ .
  Im Bild sind die beiden Ebenen $E$ und $F$ noch einmal in anderer Ansicht gezeichnet. Man kann nun eine einfache Gleichung für den Winkel $α$ zwischen den Ebenen $E$ und $F$ aufstellen:
  $α + 2 \cdot φ = 180^{\circ} \Rightarrow α = 180^{\circ} - 2 \cdot φ$ (nur Angabe eines Terms)
  Seitenansicht der beiden Ebenen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Größe von $α$ mithilfe der Normalenvektoren der Ebenen.
5. Die Ebene $E$ teilt den Quader in zwei Teilkörper.
  Bestimmen Sie das Verhältnis der Volumina der beiden Teilkörper. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Verhältnis der Volumina der beiden Teilkörper
  Der pyramidenförmige Teilkörper ist eine dreiseitige Pyramide.
  Für das Pyramidenvolumen gilt: $V_{P} = \frac{1}{3} \cdot G \cdot h$
  Die Grundfläche der Pyramide $G$ ist die Hälfte der Grundfläche $A$ des Quaders:
  $G = \frac{1}{2} \cdot A$ .
  Quader und Pyramide haben die gleiche Höhe $h$ . Das Volumen des Quaders ist $V_{Q} = A \cdot h$ .
  $\Rightarrow V_{P} = \frac{1}{3} \cdot (\frac{1}{2} \cdot A) \cdot h = \frac{1}{6} \cdot A \cdot h = \frac{1}{6} \cdot V_{Q}$
  Damit beträgt das gesuchte Verhältnis $1 : 5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für das Pyramidenvolumen gilt: $V_{P} = \frac{1}{3} \cdot G \cdot h$
  Die Grundfläche der Pyramide $G$ ist die Hälfte der Grundfläche $A$ des Quaders: $G = \frac{1}{2} \cdot A$ .
  Quader und Pyramide haben die gleiche Höhe $h$ . Das Volumen des Quaders ist $V_{Q} = A \cdot h$ .
  Setze $G$ in $V_{P}$ ein und forme so um, dass das Volumen des Quaders $V_{Q}$ abgelesen werden kann.
6. Das Saarpolygon wird von verschiedenen Positionen aus betrachtet. Die Abbildungen 1 und 2 stellen das Saarpolygon für zwei dieser Positionen schematisch dar.
  Abbildung 1
  Geben Sie zu jeder der beiden Abbildungen einen möglichen Vektor an, der die zu der Position gehörige Blickrichtung beschreibt.
  Stellen Sie das Saarpolygon schematisch für eine Betrachtung von oben dar. (4 BE)
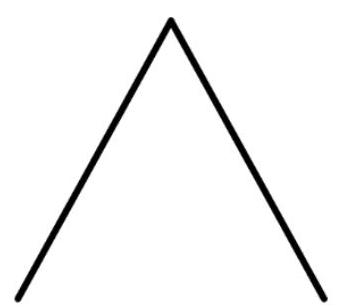
  Abbildung 2
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
  Möglicher Vektor, der die zu der Position gehörige Blickrichtung beschreibt
  Blickt man in Richtung der $x_{2}$ -Achse, so erscheint das Saarpolygon entsprechend der Abbildung $1$ .
  Ein möglicher Vektor für diese Blickrichtung ist der Vektor $(\begin{array}{c} 0 \\ - 1 \\ 0 \end{array})$ oder auch $(\begin{array}{c} 0 \\ 1 \\ 0 \end{array})$ .
  Für die Abbildung $2$ muss man in Richtung einer Winkelhalbierenden der $x_{1} x_{2}$ -Ebene blicken.
  Ein möglicher Vektor für diese Blickrichtung ist der Vektor $(\begin{array}{c} 1 \\ - 1 \\ 0 \end{array})$ oder auch $(\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$ .
  Stellen Sie das Saarpolygon schematisch für eine Betrachtung von oben dar
  Blickt man von oben auf das Saarpolygon, so erhält man die untere Abbildung.
  Oder auch in gedrehter Ansicht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. Der Punkt $P (0 | 0 | h)$ liegt innerhalb des Quaders und hat von den drei Strecken $A B, B C$ und $C D$ den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von $h$ :
  i. $\vec{O Q} = (\begin{array}{c} 11 \\ 11 \\ 0 \end{array}) + t \cdot (\begin{array}{c} - 22 \\ 0 \\ 28 \end{array}), t \in [0; 1]$
  ii. $\vec{P Q} \cdot \vec{A B} = 0$
  iii. $| P Q | = 28 - h$
  Erläutern Sie die Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von $h$ zugrunde liegen. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von $h$ zugrunde liegen
  Mit Gleichung $i$ wird ein Punkt $Q$ festgelegt, der auf der Strecke $A B$ liegt (wegen $t \in [0; 1]$ ).
  Der Punkt $P (0 | 0 | h)$ ist ein Punkt auf der $x_{3}$ -Achse. Der Vektor $\vec{P Q}$ soll senkrecht auf der Strecke $A B$ stehen (für den kürzesten Abstand der Punkte $P$ und $Q$ ). Das ist dann der Fall, wenn Gleichung $ii$ erfüllt ist.
  Die Länge von $P Q$ ist der Abstand des Punktes $P$ von $Q$ . Andererseits soll nach Aufgabenstellung der Punkt $P$ auch den gleichen Abstand zur Strecke $B C$ haben.
  Für die Punkte $B$ und $C$ ist $x_{3} = 28$ . Die $x_{3}$ -Koordinate vom Punkt $P$ ist $h$ . Der Abstand von $P$ zur Strecke $B C$ ist dann gleich $28 - h$ , wie es Gleichung $iii$ beschreibt.
  Die folgende Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur der Veranschaulichung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Mit Gleichung $i$ wird ein Punkt $Q$ festgelegt, der auf der Strecke $A B$ liegt.
  Gleichung $ii$ : $\vec{P Q} ⟂ \vec{A B}$
  Gleichung $iii$ : Der Abstand von $P$ zur Strecke $B C$ ist dann gleich $28 - h$ ,
8
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 3B
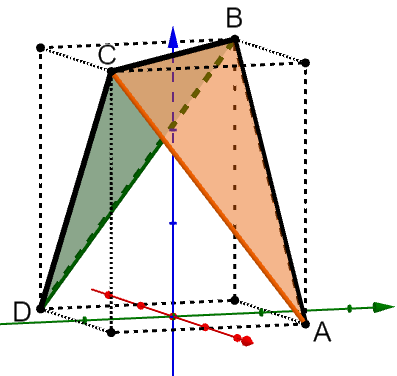
Für $k \in ℝ$ mit $0 < k \leq 6$ werden die Pyramiden $A B C D_{k}$ mit $A (0 | 0 | 0), B (4 | 0 | 0), C (0 | 4 | 0)$ und $D_{k} (0 | 0 | k)$ betrachtet (vgl. Abbildung 1).
Der Mittelpunkt der Strecke $B C$ ist $M (2 | 2 | 0)$ .
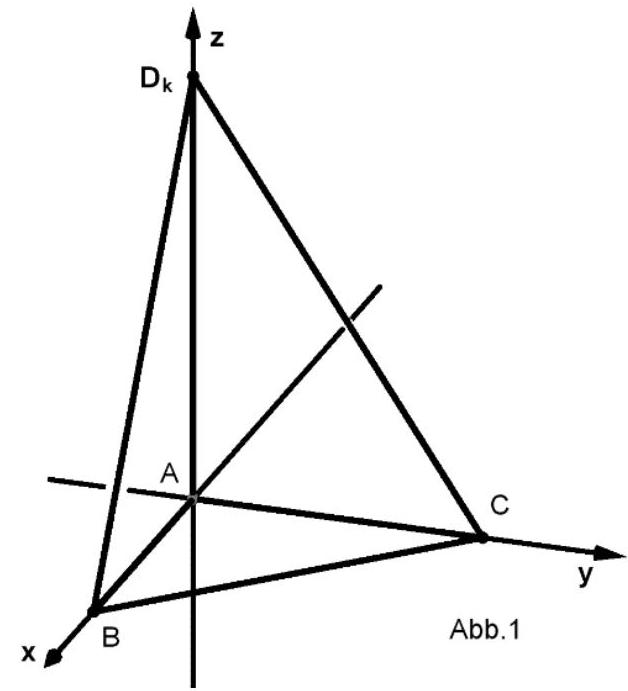
1. Begründen Sie, dass das Dreieck $B C D_{k}$ gleichschenklig ist. Berechnen Sie den Flächeninhalt des Dreiecks $B C D_{k}$ für $k = 6$ . (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck
  Begründung, dass das Dreieck $B C D_{k}$ gleichschenklig ist
  Zwei Dreiecksseiten müssen gleichlang sein.
  Berechne die Vektoren $\vec{D_{k} B}$ und $\vec{D_{k} C}$ .
  $\vec{D_{k} B} = \vec{O B} - \vec{D_{k}} = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ k \end{array}) = (\begin{array}{c} 4 \\ 0 \\ - k \end{array})$
  $\vec{D_{k} C} = \vec{O C} - \vec{D_{k}} = (\begin{array}{c} 0 \\ 4 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ k \end{array}) = (\begin{array}{c} 0 \\ 4 \\ - k \end{array})$
  Die Beträge der beiden Vektoren sind gleich groß (es treten die gleichen Vektorkoordinaten auf).
  Flächeninhalt des Dreiecks $B C D_{k}$ für $k = 6$
  Es ist $D_{6} (0 | 0 | 6)$ .
  Die Dreieckshöhe ist $| \vec{M D_{6}} |$ :
  $\vec{M D_{6}} = \vec{O D_{6}} - \vec{O M} = (\begin{array}{c} 0 \\ 0 \\ 6 \end{array}) - (\begin{array}{c} 2 \\ 2 \\ 0 \end{array}) = (\begin{array}{c} - 2 \\ - 2 \\ 6 \end{array})$
  $\Rightarrow | \vec{M D_{6}} | = \sqrt{(- 2)^{2} + (- 2)^{2} + 6^{2}} = \sqrt{44}$
  Die Basis des Dreiecks ist der Vektor $\vec{B C}$ .
  $\vec{B C} = \vec{O C} - \vec{O B} = (\begin{array}{c} 0 \\ 4 \\ 0 \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} - 4 \\ 4 \\ 0 \end{array})$
  $\Rightarrow | \vec{B C} | = \sqrt{(- 4)^{2} + 4^{2} + 0^{2}} = \sqrt{32} .$
  Für den Flächeninhalt erhält man dann:
  $A_{△} = \frac{1}{2} \cdot \sqrt{32} \cdot \sqrt{44} = 4 \cdot \sqrt{22} \approx 18,8 FE$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne die Vektoren $\vec{D_{k} B}$ und $\vec{D_{k} C}$ und vergleiche ihre Beträge.
  Teil 2
  Die Dreieckshöhe ist $| \vec{M D_{6}} |$ . Die Basis des Dreiecks ist der Vektor $\vec{B C}$ .
  Der Flächeninhalt des Dreiecks ist dann $0,5 \cdot | \vec{B C} | \cdot | \vec{M D_{6}} |$ .
2. Für jeden Wert von $k$ liegt die Seitenfläche $B C D_{k}$ in der Ebene $L_{k}$ .
  Bestimmen Sie eine Gleichung von $L_{k}$ in Koordinatenform. (4 BE)
  [Zur Kontrolle: $x + y + \frac{4}{k} \cdot z = 4$ ]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebenen
  Gleichung von $L_{k}$ in Koordinatenform
  Es ist allgemein $E : a x + b y + c z = d$
  Setze nacheinander die Koordinaten der Punkte $B (4 | 0 | 0), C (0 | 4 | 0)$ und $D_{k} (0 | 0 | k)$ ein. Man erhält ein lineares Gleichungssystem:
  $\begin{array}{rccccccc} I & a \cdot 4 & + & b \cdot 0 & + & c \cdot 0 & = & d \\ II & a \cdot 0 & + & b \cdot 4 & + & c \cdot 0 & = & d \\ III & a \cdot 0 & + & b \cdot 0 & + & c \cdot k & = & d \end{array}$
  Aus $I \Rightarrow a = \frac{d}{4}$ .
  Aus $II \Rightarrow b = \frac{d}{4}$ .
  Aus $III \Rightarrow c = \frac{d}{k}$ .
  $L_{k} : a x + b y + c z = d \Rightarrow \frac{d}{4} \cdot x + \frac{d}{4} \cdot y + \frac{d}{k} \cdot z = d$
  Für $d = 4$ folgt dann:
  $L_{k} : x + y + \frac{4}{k} \cdot z = 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist allgemein $E : a x + b y + c z = d$
  Setze nacheinander die Koordinaten der Punkte $B (4 | 0 | 0), C (0 | 4 | 0)$ und $D_{k} (0 | 0 | k)$ ein.
  Man erhält ein lineares Gleichungssystem.
3. Ermitteln Sie den Wert von $k$ , für den die Größe des Winkels, unter dem die $z$ -Achse die Ebene $L_{k}$ schneidet, $30^{\circ}$ beträgt. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
  Wert von $k$ , für den die Größe des Winkels $30^{\circ}$ beträgt
  Der Normalenvektor der z-Achse ist ${\vec{n}}_{z} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ und sein Betrag ist gleich $1$ .
  Der Normalenvektor der Ebene $L_{k}$ ist ${\vec{n}}_{L_{k}} = (\begin{array}{c} 1 \\ 1 \\ \frac{4}{k} \end{array})$ und sein Betrag ist $\sqrt{1^{2} + 1^{2} + {(\frac{4}{k})}^{2}} = \sqrt{2 + \frac{16}{k^{2}}}$ .
  Für den Schnittwinkel zwischen Gerade und Ebene gilt allgemein:
  $𝐬 𝐢 𝐧 𝛂 = \frac{| \vec{𝐧} \circ \vec{𝐮} |}{| \vec{𝐧} | \cdot | \vec{𝐮} |}$
  Setze nun $\sin 30^{\circ} = 0,5$ und die beiden Normalenvektoren und ihre Beträge ein:
  $0,5 = \frac{| (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) \circ (\begin{array}{c} 1 \\ 1 \\ \frac{4}{k} \end{array}) |}{1 \cdot \sqrt{2 + \frac{16}{k^{2}}}} \Rightarrow 0,5 = \frac{\frac{4}{k}}{\sqrt{2 + \frac{16}{k^{2}}}}$
  Der GTR liefert als Lösung $k \approx 4,898979...$ .
  Für $k \approx 4,9$ schneidet die Ebene $L_{4,9}$ die z-Achse unter einem Winkel von $30^{\circ}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Normalenvektoren der z-Achse und von der Ebene $L_{k}$ .
  Für den Schnittwinkel zwischen einer Geraden und einer Ebene gilt allgemein: $𝐬 𝐢 𝐧 𝛂 = \frac{| \vec{𝐧} \circ \vec{𝐮} |}{| \vec{𝐧} | \cdot | \vec{𝐮} |}$
  Setze $α = 30^{\circ}$ und die beiden Normalenvektoren und ihre Beträge ein und löse nach $k$ auf.
4. Zusätzlich zu den Pyramiden wird der in der nebenstehenden Abbildung gezeigte Quader betrachtet. Die Punkte $A$ und $Q (1 | 1 | 3)$ sind Eckpunkte des Quaders, die Seitenflächen des Quaders sind parallel zu den Koordinatenebenen. Für $k = 6$ enthält die Seitenfläche $B C D_{k}$ der Pyramide den Eckpunkt $Q$ des Quaders. Für kleinere Werte von $k$ schneidet die Seitenfläche $B C D_{k}$ den Quader in einem Vieleck.
  Für einen Wert von $k$ liegen die Eckpunkte $P$ und $R$ des Quaders in der Seitenfläche $B C D_{k}$ .
  Bestimmen Sie diesen Wert von $k$ .
  [Zur Kontrolle: $k = 4$ ]
  Für diesen Wert von $k$ liegt ein Punkt einer vorderen Kante ebenfalls in der
  Seitenfläche $B C D_{k}$ .
  Bestimmen Sie die Koordinaten dieses Punktes. (6 BE)
  
  Wert von $k$
  Gegeben ist $Q (1 | 1 | 3)$ . Der Punkt $P$ hat dieselben x- und z-Koordinaten wie $Q$ .
  Seine y-Koordinate ist gleich null $\Rightarrow P (1 | 0 | 3)$ .
  Setze $P (1 | 0 | 3)$ in $L_{k} : x + y + \frac{4}{k} z = 4$ ein:
  $1 + 0 + \frac{4}{k} \cdot 3 = 4 \Rightarrow \frac{12}{k} = 3 \Rightarrow k = 4$
  Für $k = 4$ liegen die Eckpunkte $P$ und $R$ des Quaders in der Seitenfläche $B C D_{4}$
  Für $k = 4$ liegt ein Punkt einer vorderen Kante ebenfalls in der Seitenfläche $B C D_{4}$ .
  Bestimmen Sie die Koordinaten dieses Punktes
  Ein Punkt auf der vorderen Kante des Quaders hat die Koordinaten $(1 | 1 | h)$ mit $0 \leq h \leq 3.$ Die Ebene lautet $L_{4} : x + y + \frac{4}{4} \cdot z = 4 \Rightarrow L_{4} : x + y + z = 4$ .
  Setze diesen Punkt in $L_{4} : x + y + z = 4$ ein:
  $1 + 1 + h = 4 \Rightarrow h = 2$
  Der gesuchte Punkt hat die Koordinaten $(1 | 1 | 2)$ .
  Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
  Skizze
  In Rot ist die Pyramide $A B C D_{6}$ gezeichnet. Der eingezeichnete Punkt $E$ hat die Koordinaten $(1 | 1 | 2)$ und liegt in der Ebene $L_{4}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Der Punkt $P$ hat dieselben x- und z-Koordinaten wie $Q$ und seine y-Koordinate ist gleich null.
  Setze $P$ in $L_{k}$ ein und bestimme $k$ .
  Teil 2
  Ein Punkt auf der vorderen Kante des Quaders hat die Koordinaten $(1 | 1 | h)$ mit $0 \leq h \leq 3.$
  Setze diesen Punkt in $L_{4}$ ein.
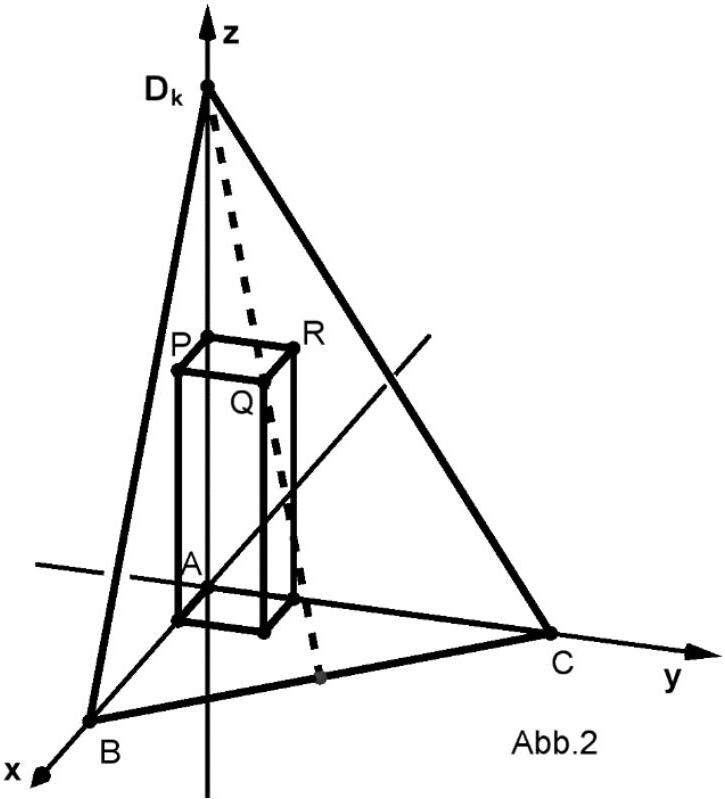
5. Geben Sie in Abhängigkeit von $k$ die Anzahl der Eckpunkte des Vielecks an, in dem die Seitenfläche $B C D_{k}$ den Quader schneidet. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von zwei Ebenen
  Anzahl der Eckpunkte des Vielecks, in dem die Seitenfläche $B C D_{k}$ den Quader schneidet
  Für $0 < k \leq 3$ werden die senkrechten Kanten zu den Punkten $P, Q$ und $R$ und die Kante auf der z-Achse geschnitten $\Rightarrow 4$ Schnittpunkte
  Für $3 < k < 4$ werden zwei Kanten im oberen Quadrat und $3$ senkrechte Kanten $P, Q$ und $R$ geschnitten $\Rightarrow 5$ Schnittpunkte
  Für $4 \leq k < 6$ werden die Kanten $P Q$ , $Q R$ und die senkrechte Kante zum Punkt $Q$ geschnitten $\Rightarrow 3$ Schnittpunkte
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege Dir, wie für $0 < k \leq 3$ die Ebene $B C D_{k}$ den Quader in welchen Kanten schneiden kann.
  Betrachte ebenso die Bereiche $3 < k < 4$ und $4 \leq k < 6$ .
6. Nun wird die Pyramide $A B C D_{6}$ betrachtet.
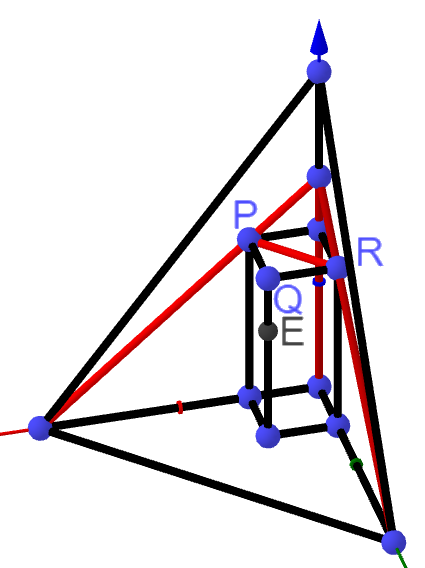
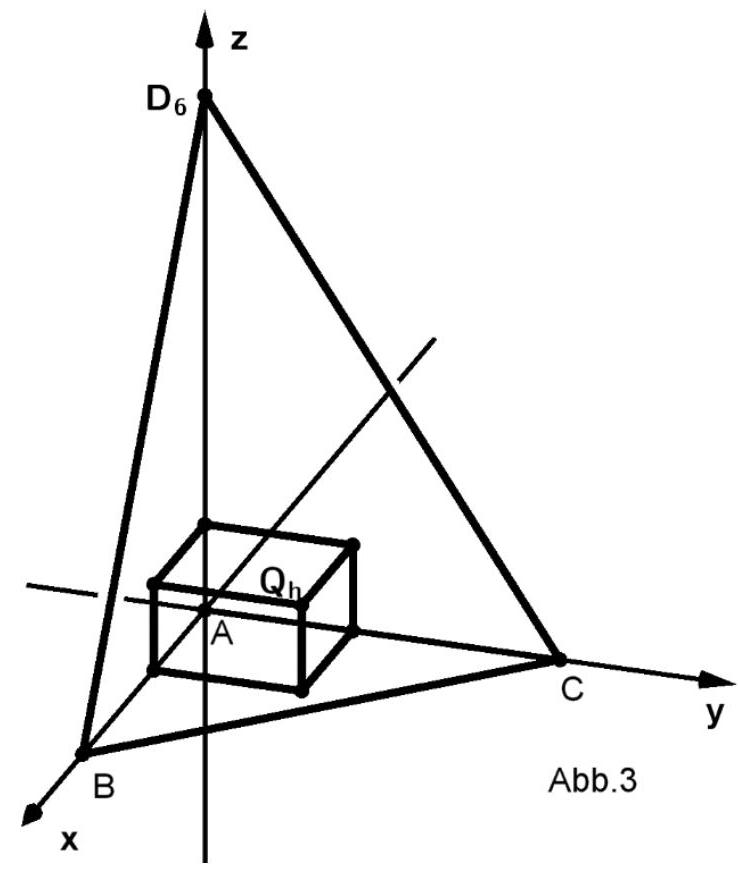
  Dieser Pyramide werden Quader einbeschrieben (vgl. Abbildung 3). Die Grundflächen der Quader liegen in der $x y$ -Ebene, haben den Eckpunkt $A$ gemeinsam und sind quadratisch.
  Die Höhe $h$ der Quader durchläuft alle reellen Werte mit $0 < h < 6$ . Für jeden Wert von $h$ liegt der Eckpunkt $Q_{h}$ in der Seitenfläche $B C D_{6}$ der Pyramide.
  Ermitteln Sie die Koordinaten des
  Punktes $Q_{h}$ . (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
  Koordinaten des Punktes $Q_{h}$
  Der Punkt $Q_{h}$ liegt auf der Strecke $M D_{6}$ .
  Der Vektor $\vec{M D_{6}} = \vec{O D_{6}} - \vec{O M} = (\begin{array}{c} 0 \\ 0 \\ 6 \end{array}) - (\begin{array}{c} 2 \\ 2 \\ 0 \end{array}) = (\begin{array}{c} - 2 \\ - 2 \\ 6 \end{array})$
  Dann gilt für $0 \leq r \leq 1$ : ${\vec{x}}_{M D_{6}} = \vec{O M} + r \cdot \vec{M D_{6}} = (\begin{array}{c} 2 \\ 2 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ - 2 \\ 6 \end{array})$
  Der Punkt $Q_{h}$ hat die z-Koordinate $h$ , dann folgt für die dritte Gleichung der Geraden:
  $h = 0 + 6 \cdot r \Rightarrow r = \frac{h}{6}$
  Eingesetzt in die Geradengleichung erhält man:
  ${\vec{x}}_{Q} = (\begin{array}{c} 2 \\ 2 \\ 0 \end{array}) + \frac{h}{6} \cdot (\begin{array}{c} - 2 \\ - 2 \\ 6 \end{array}) = (\begin{array}{c} 2 - \frac{h}{3} \\ 2 - \frac{h}{3} \\ h \end{array})$
  Also hat $Q_{h}$ die Koordinaten $(2 - \frac{h}{3} | 2 - \frac{h}{3} | h)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle eine Geradengleichung durch die Punkte $M$ und $D_{6}$ .
  Der Punkt $Q_{h}$ hat die z-Koordinate $h$ und liegt auf der Geraden.
9
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 3C
Der in der Abbildung gezeigte Körper $A B C D E F G H$ stellt einen massiven Betonkörper dar, das Rechteck $E F G H$ dessen Deckseite. Alle Außenflächen des Körpers sind eben.
An der durch die Strecke $E H$ dargestellten Oberkante des Betonkörpers ist eine Informationskarte befestigt. Die Karte kann entlang der Kante $E H$ umgeklappt werden. Liegt die Karte auf der Deckseite des Betonkörpers auf, schließt sie bündig mit den Kanten der Deckseite ab. Die Dicke der Karte soll im Folgenden vernachlässigt werden.
Gegeben sind die Punkte $A (0 | 0 | 0), B (0 | 20 | 0), E (0 | 40 | 120)$ , $F (0 | 58 | 114)$ und $H (- 20 | 40 | 120)$ .
Es gilt: $\vec{A D} = \vec{B C} = \vec{F G} = \vec{E H} = (\begin{array}{c} - 20 \\ 0 \\ 0 \end{array})$
Im verwendeten Koordinatensystem stellt die $x y$ -Ebene den horizontalen Boden dar, auf dem der Betonkörper befestigt ist. Eine Längeneinheit im Koordinatensystem entspricht $1 c m$ in der Realität.
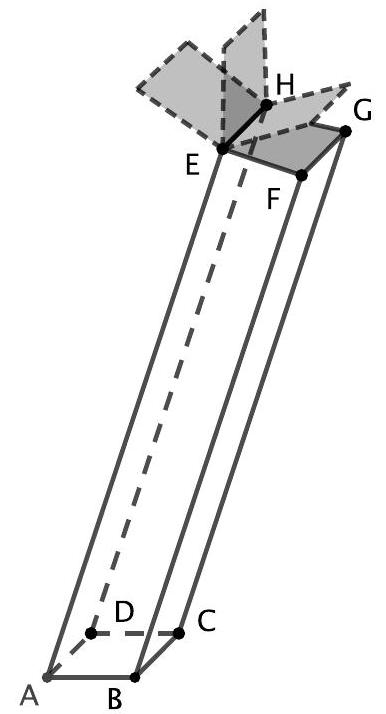
1. Zeigen Sie, dass die Kanten $A E$ und $B F$ parallel sind, und prüfen Sie, ob das Viereck $A B F E$ im Punkt $E$ einen rechten Winkel hat. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
  Zeigen Sie, dass die Kanten $A E$ und $B F$ parallel sind
  Berechne die Vektoren $\vec{A E}$ und $\vec{B F}$ :
  $\vec{A E} = \vec{O E} - \vec{O A} = (\begin{array}{c} 0 \\ 40 \\ 120 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 40 \\ 120 \end{array})$
  $\vec{B F} = \vec{O F} - \vec{O B} = (\begin{array}{c} 0 \\ 58 \\ 114 \end{array}) - (\begin{array}{c} 0 \\ 20 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 38 \\ 114 \end{array}) = \frac{19}{20} (\begin{array}{c} 0 \\ 40 \\ 120 \end{array}) = \frac{19}{20} \cdot \vec{A E}$
  Damit ist $\vec{A E} ∥ \vec{B F}$ .
  .
  Hat das Viereck $A B F E$ im Punkt $E$ einen rechten Winkel?
  Berechne das Skalarprodukt zwischen den Vektoren $\vec{A E}$ und $\vec{E F}$ :
  $\vec{E F} = \vec{O F} - \vec{O E} = (\begin{array}{c} 0 \\ 58 \\ 114 \end{array}) - (\begin{array}{c} 0 \\ 40 \\ 120 \end{array}) = (\begin{array}{c} 0 \\ 18 \\ - 6 \end{array})$
  $\vec{A E} \circ \vec{E F} = (\begin{array}{c} 0 \\ 40 \\ 120 \end{array}) \circ (\begin{array}{c} 0 \\ 18 \\ - 6 \end{array}) = 0 + 40 \cdot 18 + 120 \cdot (- 6) = 720 - 720 = 0$
  $\Rightarrow \vec{A E} ⟂ \vec{E F}$
  Im Punkt $E$ hat das Viereck einen rechten Winkel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne die Vektoren $\vec{A E}$ und $\vec{B F}$ und prüfe, ob sie Vielfache voneinander sind.
  Teil 2
  Berechne das Skalarprodukt zwischen den Vektoren $\vec{A E}$ und $\vec{E F}$ .
2. Ermitteln Sie eine Gleichung der Ebene, in der das Rechteck $E F G H$ liegt, in Koordinatenform. (3 BE)
  [Zur Kontrolle: $y + 3 \cdot z = 400]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatenform der Ebene (Kurs mit integrierten Aufgaben) (5|5)
  Gleichung der Ebene, in der das Rechteck $E F G H$ liegt, in Koordinatenform
  Es ist $\vec{n} \circ \vec{E F} = 0$ und $\vec{n} \circ \vec{E H} = 0$ .
  $\vec{E H} = \vec{O H} - \vec{O E} = (\begin{array}{c} - 20 \\ 40 \\ 120 \end{array}) - (\begin{array}{c} 0 \\ 40 \\ 120 \end{array}) = (\begin{array}{c} - 20 \\ 0 \\ 0 \end{array})$
  $\Rightarrow \vec{n} \circ (\begin{array}{c} 0 \\ 18 \\ - 6 \end{array}) = 0$ und $\vec{n} \circ (\begin{array}{c} - 20 \\ 0 \\ 0 \end{array}) = 0$
  Man erhält zwei Gleichungen:
  $18 \cdot n_{2} - 6 \cdot n_{3} = 0$ und $- 20 \cdot n_{1} = 0 \Rightarrow n_{1} = 0$
  $n_{3}$ ist frei wählbar, z.B. $n_{3} = 3 \Rightarrow 18 \cdot n_{2} - 6 \cdot 3 = 0 \Rightarrow n_{2} = 1$
  Der Vektor $\vec{n} = (\begin{array}{c} 0 \\ 1 \\ 3 \end{array})$ .
  Mit diesem Normalenvektor ist $E : y + 3 z = c$
  Setze z.B. den Punkt $E (0 | 40 | 120)$ ein, der in der Ebene liegt.
  $\Rightarrow 40 + 3 \cdot 120 = c \Rightarrow c = 400$
  Damit ist $E_{E F G H} : y + 3 z = 400$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $\vec{n} \circ \vec{E F} = 0$ und $\vec{n} \circ \vec{E H} = 0$ .
  Man erhält zwei Gleichungen, um den Vektor $\vec{n}$ zu bestimmen.
  Mit diesem Vektor $\vec{n}$ und einem Punkt, der in der Ebene liegt, kann die Ebenengleichung ermittelt werden.
3. Auf den Betonkörper treffendes Sonnenlicht kann im Modell durch parallele Geraden beschrieben werden. Der Richtungsvektor dieser Geraden ist $(\begin{array}{c} - 2 \\ 1 \\ - 3 \end{array})$ .
  Die Karte wird so positioniert, dass sie vertikal steht (vgl. Abbildung). Durch den Eckpunkt $K$ wird ein Schattenpunkt $K^{'}$ auf der Deckseite des Betonkörpers erzeugt.
  Ermitteln Sie die Koordinaten von $K^{'}$ .
  (6 BE)
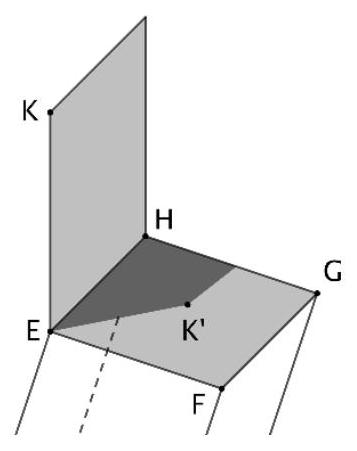
  Mit Ausnahme der Position, die in der Teilaufgabe c) betrachtet wurde, können alle
  Positionen der Karte jeweils durch eine der Ebenen $E_{a} : a \cdot y + z = 40 \cdot a + 120$ mit $a \in ℝ$ beschrieben werden.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Koordinaten von $K^{'}$
  Der Punkt $K$ hat die gleichen x- und y-Koordinaten wie der Punkt $E$ .
  Die z-Koordinate von $K$ ist gleich der vom Punkt $E$ verlängert um $| \vec{E F} |$ :
  $K (0 | 40 | 120 + | \vec{E F} |)$
  Mit $\vec{E F} = (\begin{array}{c} 0 \\ 18 \\ - 6 \end{array})$ (aus Aufgabe a)) folgt für den Betrag:
  $| \vec{E F} | = \sqrt{0^{2} + 18^{2} + (- 6)^{2}} = \sqrt{360} = 6 \cdot \sqrt{10}$
  Geradengleichung
  Dann ergibt sich die Geradengleichung des Sonnenlichtes durch den Punkt $K$ mit dem gegebenen Richtungsvektor:
  $g : \vec{x} = (\begin{array}{c} 0 \\ 40 \\ 120 + 6 \cdot \sqrt{10} \end{array}) + r \cdot (\begin{array}{c} - 2 \\ 1 \\ - 3 \end{array})$
  Wert des Parameters und Koordinaten von $K^{'}$
  Die Gerade $g$ muss mit der Ebene $E : y + 3 \cdot z = 400$ aus Aufgabe b) geschnitten werden, um den Punkt $K^{'}$ zu erhalten:
  Einsetzen von $g$ in $E$ liefert die Gleichung:
  $40 + r + 3 \cdot (120 + 6 \cdot \sqrt{10} - 3 r) = 400$
  Der GTR liefert als Lösung $r \approx 7,115124...$ .
  Damit ist $r \approx 7,12$ .
  Die Koordinaten von $K^{'}$ ergeben sich durch Einsetzen von $r \approx 7,12$ in die Geradengleichung:
  $\vec{O K^{'}} = (\begin{array}{c} 0 - 2 \cdot 7,12 \\ 40 + 7,12 \\ 120 + 6 \cdot \sqrt{10} - 3 \cdot 7,12 \end{array}) \approx (\begin{array}{c} - 14,24 \\ 47,12 \\ 117,61 \end{array}) \approx (\begin{array}{c} - 14 \\ 47 \\ 118 \end{array})$
  Der Punkt $K^{'}$ hat etwa die Koordinaten $K^{'} (- 14 | 47 | 118)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Koordinaten des Punktes $K$ .
  Erstelle die Geradengleichung durch den Punkt $K$ mit dem gegebenen Richtungsvektor des Sonnenlichtes.
  Schneide die Gerade mit der Ebene $E_{E F G H}$ .
  Setze den erhaltenen Parameter in die Geradengleichung ein, um die Koordinaten des gesuchten Punktes $K^{'}$ zu erhalten.
4. Ermitteln Sie denjenigen Wert von $a$ , für den die Karte auf der Deckseite des Betonkörpers liegt. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkte in der Ebene
  Wert von $a$ , für den die Karte auf der Deckseite des Betonkörpers liegt
  Setze die Koordinaten von $F (0 | 58 | 114)$ in die Ebenengleichung $E_{a} : a \cdot y + z = 40 \cdot a + 120$ ein.
  $a \cdot 58 + 114$ $=$ $40 \cdot a + 120$ $- 40 \cdot a$
  ↓
  Löse nach $a$ auf.
  $18 \cdot a + 114$ $=$ $120$ $- 114$
  $18 \cdot a$ $=$ $6$ $: 18$
  $a$ $=$ $\frac{1}{3}$
  Für $a = \frac{1}{3}$ liegt die Karte auf der Deckseite des Betonkörpers.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze die Koordinaten von $F (0 | 58 | 114)$ in die Ebenengleichung $E_{a} : a \cdot y + z = 40 \cdot a + 120$ ein und löse nach $a$ auf.
5. Geben Sie die Bedeutung der Lösung der Gleichung $(\begin{array}{c} - 2 \\ 1 \\ - 3 \end{array}) \cdot (\begin{array}{l} 0 \\ a \\ 1 \end{array}) = 0$ bezüglich der Position der Karte zum Sonnenlicht an.
  Beschreiben Sie für diese Position den durch die Karte auf die Deckseite fallenden Schatten. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Bedeutung der Lösung der Gleichung
  $(\begin{array}{c} - 2 \\ 1 \\ - 3 \end{array}) \cdot (\begin{array}{l} 0 \\ a \\ 1 \end{array}) = 0$
  Der erste Vektor ist der Richtungsvektor des Sonnenlichtes. Der zweite Vektor ist der Normalenvektor der Ebene $E_{a}$ . Wenn das Skalarprodukt den Wert null hat, dann stehen diese beiden Vektoren senkrecht aufeinander. Das hat zur Folge, dass die Ebene, die die Karte darstellt, parallel zum Sonnenlicht verläuft.
  Beschreibung des Schattens
  Da die Ebene, die die Karte darstellt, parallel zum Sonnenlicht verläuft, fällt kein Schatten von dieser Karte auf die Deckfläche des Betonkörpers.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Der erste Vektor ist der Richtungsvektor des Sonnenlichtes. Der zweite Vektor ist der Normalenvektor der Ebene $E_{a}$ .
  Untersuche das Skalarprodukt der Vektoren.
  Teil 2
  Verläuft eine Ebene parallel zu den Sonnenstrahlen, dann wirft sie keinen Schatten.
6. Liegt die Karte auf der Deckseite des Betonkörpers, wird einer ihrer Eckpunkte durch $F$ dargestellt. Dieser Eckpunkt nimmt während des Umklappens verschiedene Positionen ein. Zwei dieser Positionen werden durch $P (0 | y_{1} | z)$ und $Q (0 | y_{2} | z)$ mit $y_{2} < y_{1}$ beschrieben, wobei $| \vec{F P} | = y_{1} - y_{2}$ gilt.
  Begründen Sie, ohne zu rechnen, dass die Strecken $E F$ und $E Q$ einen doppelt so großen Winkel einschließen wie die Strecken $E F$ und $E P$ , und veranschaulichen Sie Ihre Begründung durch eine geeignet beschriftete Skizze. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kongruenz
  Begründung, dass die Strecken $E F$ und $E Q$ einen doppelt so großen Winkel einschließen wie die Strecken $E F$ und $E P$
  Zwei dieser Positionen werden durch $P (0 | y_{1} | z)$ und $Q (0 | y_{2} | z)$ mit $y_{2} < y_{1}$ beschrieben. Bei den beiden Punkten sind die x- und y-Koordinaten gleich groß. Somit stellt $y_{2} - y_{1}$ ihren Abstand dar. Andererseits ist $| \vec{F P} | = y_{1} - y_{2}$ .
  Skizze in der y-z-Ebene:
  Skizze zur Aufgabe
  Welche Informationen haben wir?
  Die folgenden Strecken sind gleich groß, d.h. $E F = E P = E Q$ , da es sich um den Drehradius handelt.
  Weiterhin sind laut Aufgabentext die Strecken $P Q = F P$ .
  Damit sind die beiden Dreiecke $E F P$ und $E P Q$ zueinander kongruent und liegen bzgl. der Strecke $E P$ achsensymmetrisch zueinander.
  Der Winkel im Viereck $E F P Q$ im Eckpunkt $E$ ist somit doppelt so groß, wie der eines der Dreiecke im Eckpunkt $E$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Weise nach, dass die beiden Dreiecke $E F P$ und $E P Q$ zueinander kongruent sind.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$P (X \leq 1)$	$>$	$0,99$
	↓	Verwenden das Gegenereignis "Es ist kein Armband kaputt"
$1 - P (X = 0)$	$>$	$0,99$	$- 0,99$
$0,01 - P (X = 0)$	$>$	$0$	$+ P (X = 0)$
$0,01$	$>$	$P (X = 0)$
	↓	Binomialverteilung mit $n$ , $p = 0,1$ und $k = 0$
$0,01$	$>$	$(\binom{n}{0}) \cdot {0,1}^{0} \cdot {0,9}^{n}$
	↓	Binomialkoeffizient ist $1$ und ${0,1}^{0} = 1$
$0,01$	$>$	$1 \cdot 1 \cdot {0,9}^{n}$
$0,01$	$>$	${0,9}^{n}$	$\log_{0,9} ()$
	↓	Beim Anwenden vom Logarithmus mit einer Basis kleiner $1$ wird das Ungleichzeichen gedreht.
$\log_{0,9} (0,01)$	$<$	$n$
$43,7...$	$<$	$n$

$e$	$=$	$e^{- \frac{1}{2} a \cdot 1^{2} + \frac{1}{2}}$
$e^{1}$	$=$	$e^{- \frac{1}{2} a + \frac{1}{2}}$

$f_{a} (x)$	$=$	$x \cdot e^{- \frac{1}{2} a \cdot x^{2} + \frac{1}{2}}$
	↓	Setze $x = + \sqrt{\frac{1}{a}}$ ein.
$f_{a} (+ \sqrt{\frac{1}{a}})$	$=$	$+ \sqrt{\frac{1}{a}} \cdot e^{- \frac{1}{2} a \cdot {(+ \sqrt{\frac{1}{a}})}^{2} + \frac{1}{2}}$
	↓	Vereinfache die Potenz.
	$=$	$+ \sqrt{\frac{1}{a}} \cdot e^{- \frac{1}{2} a \cdot (\frac{1}{a}) + \frac{1}{2}}$
	↓	Kürze in der Potenz.
	$=$	$+ \sqrt{\frac{1}{a}} \cdot e^{- \frac{1}{2} + \frac{1}{2}}$
	$=$	$+ \sqrt{\frac{1}{a}} \cdot e^{0}$
	↓	Es ist $e^{0} = 1$ .
	$=$	$+ \sqrt{\frac{1}{a}}$

$h_{a} (x)$	$=$	$(1 - a \cdot x) \cdot e^{2 \cdot a \cdot x}$
	↓	Setze $x = \frac{1}{2 a}$ ein.
$h_{a} (\frac{1}{2 a})$	$=$	$(1 - a \cdot \frac{1}{2 a}) e^{2 a \cdot \frac{1}{2 a}}$
	↓	Kürze mit $a$ .
	$=$	$(1 - \frac{1}{2}) e^{\frac{2}{2}}$
	↓	Fasse zusammen.
	$=$	$\frac{1}{2} \cdot e^{1}$

$(1 - a x) \cdot e^{2 \cdot a \cdot x}$	$=$	$a \cdot (1 - 2 a x) \cdot e^{2 a x}$
$1 - a x$	$=$	$a \cdot (1 - 2 a x)$
	↓	Löse die Klammer auf.
$1 - a x$	$=$	$a - 2 a^{2} x$	$+ a x - a$
$1 - a$	$=$	$a x - 2 a^{2} x$
	↓	Klammere $a x$ aus.
$1 - a$	$=$	$x a (1 - 2 a)$

$P (114 \leq X \leq 126)$	$=$	$\underset{Taschenrechner}{\underset{⏟}{F_{600; 0,2} (k = 126) - F_{600; 0,2} (k = 113)}}$
	$\approx$	$0,7483 - 0,2554$
	$=$	$49,29 %$

$0,15$	$=$	$P (X \leq 3)$
	↓	Ist das Integral von $- \infty$ bis $3$
$0,15$	$=$	$\int_{- \infty}^{3} φ_{μ; 1,25} (x) d x$
	↓	Bestimmt der Taschenrechner
$μ$	$\approx$	$4,3$

$P_{F} (D)$	$=$	$\frac{P (D \cap F)}{P (F)}$
	↓	$P (F)$ von oben
	$=$	$\frac{P (D \cap F)}{0,3257}$
	↓	Baumdiagramm
	$=$	$\frac{0,59 \cdot 0,23}{0,3257}$
	$\approx$	$0,4166$

Verwenden des Gegenereignis
	↓
$P (X > 50)$	$=$	$1 - P (X \leq 50)$
	↓	Verwenden der Verteilungsfunktion
	$=$	$1 - F_{100; 0,59} (50)$
	↓	Taschenrechner
	$=$	$1 - 0,0427...$
	$\approx$	$95,72 %$

$P_{2 n} (X = 0)$	$=$	$(\binom{2 n}{0}) \cdot {0,59}^{0} \cdot {0,41}^{2 n - 0}$
	↓	Binomialkoeffizient ist 1. Außerdem ${0,59}^{0} = 1$
	$=$	$1 \cdot 1 \cdot {0,41}^{2 n}$
	$=$	${0,41}^{2 n}$

$P_{n} (X = 0)$	$=$	$(\binom{2 n}{0}) \cdot {0,59}^{0} \cdot {0,41}^{n - 0}$
	↓	Binomialkoeffizient ist 1. Außerdem ${0,59}^{0} = 1$
	$=$	$1 \cdot 1 \cdot {0,41}^{n}$
	$=$	${0,41}^{n}$

	$\frac{P (unrund, zwei mal nicht aussortiert)}{P (aussortiert)}$
	↓ Baumdiagramm
$=$	$\frac{0,02 \cdot 0,1 \cdot 0,1}{0,98 \cdot 0,95 \cdot 0,95 + 0,02 \cdot 0,1 \cdot 0,1}$
$\approx$	$0,00023$

	$P (Regel I erfüllt)$
	↓ Teilaufgabe (g)
$=$	$\underset{Alle Bälle in [2,67;2,77]}{\underset{⏟}{{0,8315}^{24}}} + \underset{Ein Ball in [2,60;2,67] \cup [2,77; 2,85]}{\underset{⏟}{{0,8315}^{23} \cdot 0,1680 \cdot 24}}$
$=$	$0,07$

$\cos (φ) x$	$=$	$\frac{\| \vec{𝐧} \circ \vec{𝐦} \|}{\| \vec{𝐧} \| \cdot \| \vec{𝐦} \|}$
	↓	Setze die Werte für die Vektoren und ihre Beträge ein.
	$=$	$\frac{\| (\begin{array}{c} 14 \\ 14 \\ 11 \end{array}) \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) \|}{\sqrt{513} \cdot 1}$
	↓	Berechne das Skalarprodukt.
	$=$	$\frac{\| 0 + 0 + 11 \|}{\sqrt{513}}$
	$=$	$\frac{11}{\sqrt{513}}$

${0,41}^{2 n} \cdot 2$	$=$	${0,41}^{n}$	$: {0,41}^{n}$
$\frac{{0,41}^{2 n}}{{0,41}^{n}} \cdot 2$	$=$	$1$
	↓	Potengesetze
${0,41}^{n} \cdot 2$	$=$	$1$	$: 2$
${0,41}^{n}$	$=$	$\frac{1}{2}$

Gegenereignis
	↓
$P (X \geq 1)$	$=$	$1 - P (X = 0)$
	↓	Binomialverteilung
	$\approx$	$1 - 0,3487$
	$=$	$0,6513$

Verteilungsfunktion
	↓
$P (Z \leq 1)$	$=$	$F_{5; 0,6513} (1)$
	↓	Taschenrechner
	$\approx$	$0,0533$

$μ$	$=$	$n \cdot p$
	↓	$n = 200, p = 0,02$ ( $2 %$ der Bälle sind unrund)
	$=$	$200 \cdot 0,02$
	$=$	$4$

Umformuliert
	↓
$P (X < 4)$	$=$	$P (X \leq 3)$
	↓	Verteilungsfunktion
	$=$	$F_{200; 0,02} (3)$
	↓	Taschenrechner (BinomialCDF)
	$\approx$	$0,4315$

Verwende das Gegenereignis
	↓
$P (X > 6)$	$=$	$1 - P (X \leq 6)$
	↓	Verteilungsfunktion der Binomialverteilung
	$=$	$1 - F_{200; 0,02} (6)$
	↓	Taschenrechner (BinomialCDF)
	$\approx$	$1 - 0,8914$
	$\approx$	$0,1086$

	$1 - {(P (X \leq 6))}^{2}$
	↓ Einsetzen der Wahrscheinlichkeit
$=$	$1 - {0,8914}^{2}$
$\approx$	$0,2054$

$a \cdot 58 + 114$	$=$	$40 \cdot a + 120$	$- 40 \cdot a$
	↓	Löse nach $a$ auf.
$18 \cdot a + 114$	$=$	$120$	$- 114$
$18 \cdot a$	$=$	$6$	$: 18$
$a$	$=$	$\frac{1}{3}$

Wahlteil - GTR

Aufgabe 1A

Berechnen der Nullstelle

Hast du eine Frage oder Feedback?

Sachverhalt analysieren

Hast du eine Frage oder Feedback?

Begründung

Hast du eine Frage oder Feedback?

Berechnung von a

Berechnung des Winkels, den der Graph von fa mit der Parallelen zur x-Achse durch den Punkt P einschließt

Hast du eine Frage oder Feedback?

Verlauf der Graphen

Hast du eine Frage oder Feedback?

Anzahl der Wendestellen von fa nach dem Wert von a∈ℝ

Hast du eine Frage oder Feedback?

Der entstehende Graph

Hast du eine Frage oder Feedback?

Lösung

Hast du eine Frage oder Feedback?

Begründung, dass es sich dabei um die Gerade mit der Gleichung y=x handelt

Hast du eine Frage oder Feedback?

Berechne den Wert von a, für den das Viereck den Flächeninhalt 144 hat

Hast du eine Frage oder Feedback?

Aufgabe 1B

Fünfjahreszeiträume

Hast du eine Frage oder Feedback?

Exponentielle Regression

Logistische Regression

Hast du eine Frage oder Feedback?

Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 kann mit dem folgenden Term bestimmt werden: 1490+∫020g(x)dx

Hast du eine Frage oder Feedback?

Skizze des Koordinatensystems

Hast du eine Frage oder Feedback?

Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005

Hast du eine Frage oder Feedback?

Maximaler Schuldenstand sowie das Jahr, in dem dieser erreicht wird

Hast du eine Frage oder Feedback?

Nachweis für a≠0, dass der maximale Funktionswert unabhängig vom Wert von a ist

Hast du eine Frage oder Feedback?

y-Koordinate dieses gemeinsamen Punktes mithilfe einer Skizze ohne Berechnung der Geradengleichungen

Hast du eine Frage oder Feedback?

Werte von a, für die der Graph der Ableitungsfunktion ha′ vollständig unterhalb des Graphen der Funktion ha liegt

Hast du eine Frage oder Feedback?

Aufgabe 1C

Geschwindigkeit, die der ICE eine halbe Minute nach 15: 00 Uhr hat.

Nachweis, dass die Geschwindigkeit in der ersten halben Minute nach 15: 00 Uhr um einen kleineren Betrag abnimmt als in der darauf folgenden halben Minute

Hast du eine Frage oder Feedback?

Länge des Zeitraumes, in dem die Geschwindigkeit höchstens 200, aber mindestens 150 Kilometer pro Stunde beträgt

Hast du eine Frage oder Feedback?

Mögliche Werte x1 und x2 an, sodass gilt: f′(x1)=f′(x2)

Aussage f′(x1)=f′(x2) im Sachzusammenhang

Hast du eine Frage oder Feedback?

Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt

Hast du eine Frage oder Feedback?

Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15: 03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau 7 km zurücklegt

Hast du eine Frage oder Feedback?

Prüfung der Aussage

Steigung um 15:01 Uhr

Zurückgelegter Weg

Hast du eine Frage oder Feedback?

Passende Werte von a,b und c

Hast du eine Frage oder Feedback?

Wert des Terms ∫−22s(x)dx

Beschreibung mithilfe der Abbildung 2, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann

Hast du eine Frage oder Feedback?

Untersuchung, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von s ist

Hast du eine Frage oder Feedback?

Aufgabe 2A

Informationen aus der Aufgabenstellung

Vollständige Tabelle

Hast du eine Frage oder Feedback?

Bedingte Wahrscheinlichkeit ermitteln

Hast du eine Frage oder Feedback?

Berechnung des Anteils

Hast du eine Frage oder Feedback?

Beschreibung des Terms

Hast du eine Frage oder Feedback?

Erwartungswert

Bereich der Abweichung

Wahrscheinlichkeit für die Abweichung

Berechnung von $a$

Berechnung des Winkels, den der Graph von $f_{a}$ mit der Parallelen zur $x$ -Achse durch den Punkt $P$ einschließt

Anzahl der Wendestellen von $f_{a}$ nach dem Wert von $a \in ℝ$

Begründung, dass es sich dabei um die Gerade mit der Gleichung $y = x$ handelt

Berechne den Wert von $a$ , für den das Viereck den Flächeninhalt 144 hat

Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 kann mit dem folgenden Term bestimmt werden: $1490 + \int_{0}^{20} g (x) d x$

Nachweis für $a \neq 0$ , dass der maximale Funktionswert unabhängig vom Wert von $a$ ist

Werte von $a$ , für die der Graph der Ableitungsfunktion $h_{a}^{'}$ vollständig unterhalb des Graphen der Funktion $h_{a}$ liegt

Mögliche Werte $x_{1}$ und $x_{2}$ an, sodass gilt: $f^{'} (x_{1}) = f^{'} (x_{2})$

Aussage $f^{'} (x_{1}) = f^{'} (x_{2})$ im Sachzusammenhang

Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15: 03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau $7 k m$ zurücklegt

Passende Werte von $a, b$ und $c$

Wert des Terms $\int_{- 2}^{2} s (x) d x$

Untersuchung, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von $s$ ist

Wahrscheinlichkeit $P (X \geq 5)$

Wahrscheinlichkeit $P (X > 50)$

Werte für $a$ und $b$

Wert für $n$

Wahrscheinlichkeit $P (X \leq 1)$

Wahrscheinlichkeit $P (X < 4)$

Wahrscheinlichkeit $P (X > 6)$

Wahrscheinlichkeit, dass das Gewicht in $[2,67; 2,77]$ liegt

Begründung, dass die Punkte $B$ und $C$ symmetrisch bezüglich der $x_{3}$ -Achse liegen

Gleichung von $E$ in Koordinatenform

Größe $α$ des Winkels, unter dem $E$ die $x_{1} x_{2}$ -Ebene schneidet

Geben Sie einen Term an, mit dem aus $α$ die Größe des Winkels zwischen den Ebenen $E$ und $F$ berechnet werden kann

Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von $h$ zugrunde liegen

Begründung, dass das Dreieck $B C D_{k}$ gleichschenklig ist