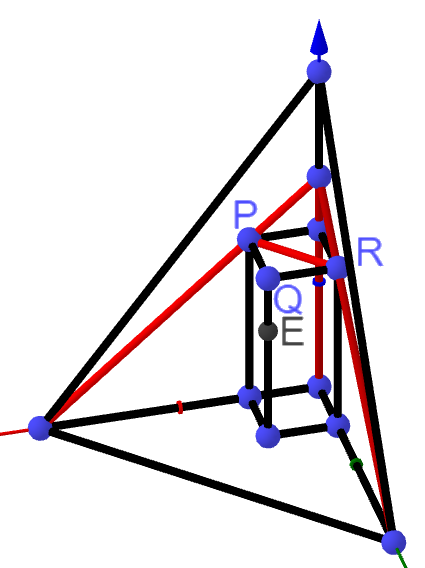
Aufgabe 3B
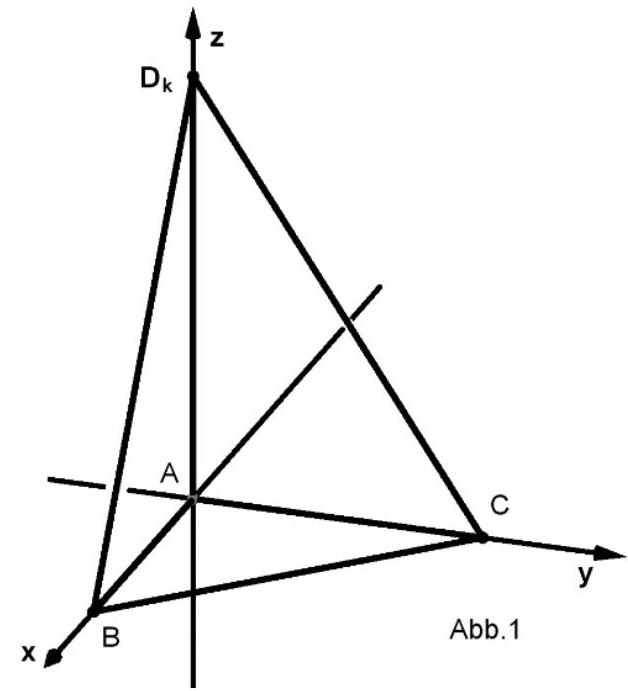
Für mit werden die Pyramiden mit und betrachtet (vgl. Abbildung 1).
Der Mittelpunkt der Strecke ist .
Begründen Sie, dass das Dreieck gleichschenklig ist. Berechnen Sie den Flächeninhalt des Dreiecks für . (5 BE)
Für jeden Wert von liegt die Seitenfläche in der Ebene .
Bestimmen Sie eine Gleichung von in Koordinatenform. (4 BE)
[Zur Kontrolle: ]
Ermitteln Sie den Wert von , für den die Größe des Winkels, unter dem die -Achse die Ebene schneidet, beträgt. (3 BE)
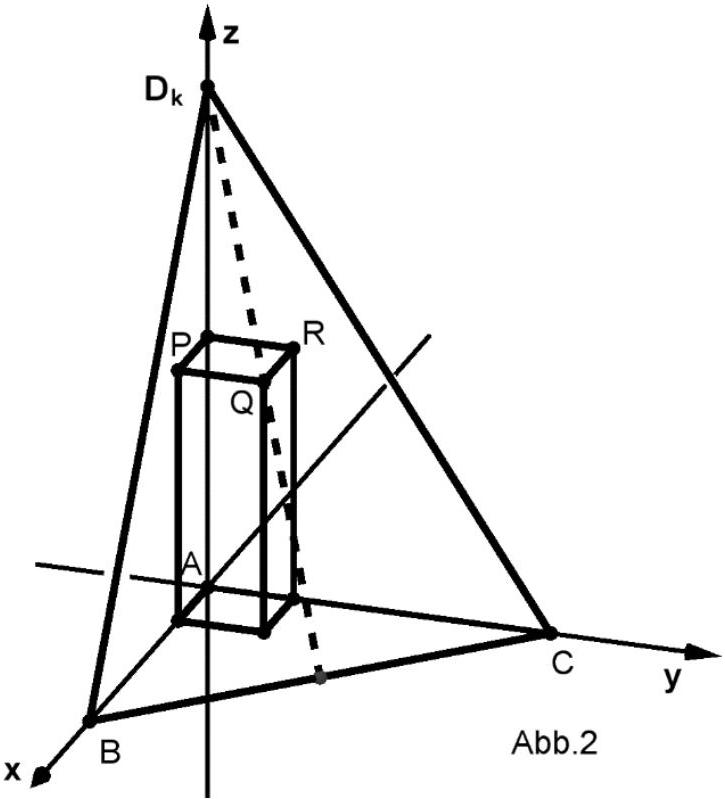
Zusätzlich zu den Pyramiden wird der in der nebenstehenden Abbildung gezeigte Quader betrachtet. Die Punkte und sind Eckpunkte des Quaders, die Seitenflächen des Quaders sind parallel zu den Koordinatenebenen. Für enthält die Seitenfläche der Pyramide den Eckpunkt des Quaders. Für kleinere Werte von schneidet die Seitenfläche den Quader in einem Vieleck.
Für einen Wert von liegen die Eckpunkte und des Quaders in der Seitenfläche .
Bestimmen Sie diesen Wert von .
[Zur Kontrolle: ]
Für diesen Wert von liegt ein Punkt einer vorderen Kante ebenfalls in der
Seitenfläche .
Bestimmen Sie die Koordinaten dieses Punktes. (6 BE)
Geben Sie in Abhängigkeit von die Anzahl der Eckpunkte des Vielecks an, in dem die Seitenfläche den Quader schneidet. (3 BE)
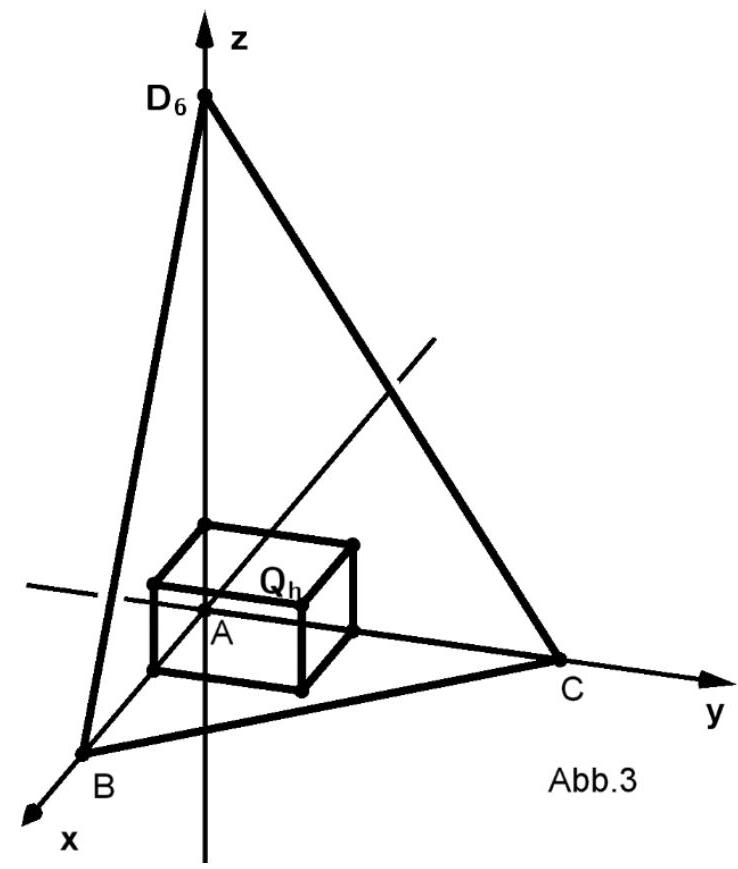
Nun wird die Pyramide betrachtet.
Dieser Pyramide werden Quader einbeschrieben (vgl. Abbildung 3). Die Grundflächen der Quader liegen in der -Ebene, haben den Eckpunkt gemeinsam und sind quadratisch.
Die Höhe der Quader durchläuft alle reellen Werte mit . Für jeden Wert von liegt der Eckpunkt in der Seitenfläche der Pyramide.
Ermitteln Sie die Koordinaten des
Punktes . (4 BE)