Wahlteil - GTR - lernen mit Serlo!

Aufgabe 3C

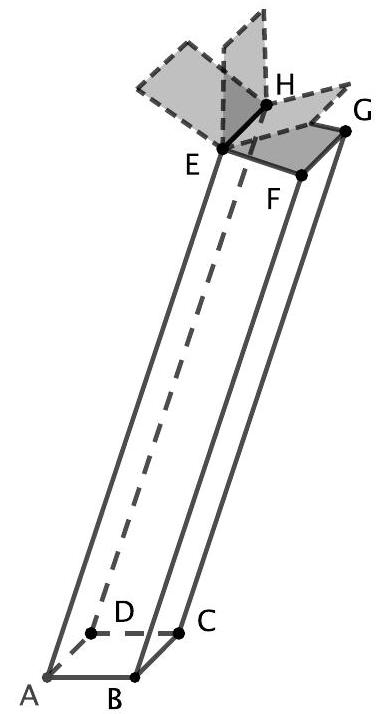
Der in der Abbildung gezeigte Körper $A B C D E F G H$ stellt einen massiven Betonkörper dar, das Rechteck $E F G H$ dessen Deckseite. Alle Außenflächen des Körpers sind eben.

An der durch die Strecke $\overline{E H}$ dargestellten Oberkante des Betonkörpers ist eine Informationskarte befestigt. Die Karte kann entlang der Kante $\overline{E H}$ umgeklappt werden. Liegt die Karte auf der Deckseite des Betonkörpers auf, schließt sie bündig mit den Kanten der Deckseite ab. Die Dicke der Karte soll im Folgenden vernachlässigt werden.

Gegeben sind die Punkte $A(0|0| 0), B(0|20| 0), E(0|40| 120)$ , $F(0|58| 114)$ und $H(-20|40| 120)$ .

Es gilt: $\def\arraystretch{1.25} \overrightarrow{A D}=\overrightarrow{B C}=\overrightarrow{F G}=\overrightarrow{E H}=\left(\begin{array}{c}-20 \\ 0 \\ 0\end{array}\right)$

Im verwendeten Koordinatensystem stellt die $x y$ -Ebene den horizontalen Boden dar, auf dem der Betonkörper befestigt ist. Eine Längeneinheit im Koordinatensystem entspricht $1 \mathrm{~cm}$ in der Realität.

Zeigen Sie, dass die Kanten $\overline{A E}$ und $\overline{B F}$ parallel sind, und prüfen Sie, ob das Viereck $A B F E$ im Punkt $E$ einen rechten Winkel hat. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Zeigen Sie, dass die Kanten $\overline{A E}$ und $\overline{B F}$ parallel sind
Berechne die Vektoren $\overrightarrow{A E}$ und $\overrightarrow{BF}$ :
$\overrightarrow{A E}= \overrightarrow{O E}- \overrightarrow{OA}=\begin{pmatrix}0\\40\\120\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}=\begin{pmatrix}0\\40\\120\end{pmatrix}$
$\overrightarrow{BF}= \overrightarrow{O F}- \overrightarrow{OB}=\begin{pmatrix}0\\58\\114\end{pmatrix}-\begin{pmatrix}0\\20\\0\end{pmatrix}=\begin{pmatrix}0\\38\\114\end{pmatrix}=\dfrac{19}{20}\begin{pmatrix}0\\40\\120\end{pmatrix}=\dfrac{19}{20}\cdot \overrightarrow{A E}$
Damit ist $\overrightarrow{A E}\parallel \overrightarrow{BF}$ .
.
Hat das Viereck $ABFE$ im Punkt $E$ einen rechten Winkel?
Berechne das Skalarprodukt zwischen den Vektoren $\overrightarrow{A E}$ und $\overrightarrow{EF}$ :
$\overrightarrow{EF}= \overrightarrow{OF}- \overrightarrow{OE}=\begin{pmatrix}0\\58\\114\end{pmatrix}-\begin{pmatrix}0\\40\\120\end{pmatrix}=\begin{pmatrix}0\\18\\-6\end{pmatrix}$
$\overrightarrow{AE}\circ\overrightarrow{EF}=\begin{pmatrix}0\\40\\120\end{pmatrix}\circ\begin{pmatrix}0\\18\\-6\end{pmatrix}=0+40\cdot 18+120\cdot(-6)=720-720=0$
$\Rightarrow\;\overrightarrow{AE}\perp\overrightarrow{EF}$
Im Punkt $E$ hat das Viereck einen rechten Winkel.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne die Vektoren $\overrightarrow{A E}$ und $\overrightarrow{BF}$ und prüfe, ob sie Vielfache voneinander sind.
Teil 2
Berechne das Skalarprodukt zwischen den Vektoren $\overrightarrow{A E}$ und $\overrightarrow{EF}$ .
Ermitteln Sie eine Gleichung der Ebene, in der das Rechteck $E F G H$ liegt, in Koordinatenform. (3 BE)
[Zur Kontrolle: $y+3 \cdot z=400]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatenform der Ebene (Kurs mit integrierten Aufgaben) (5|5)
Gleichung der Ebene, in der das Rechteck $E F G H$ liegt, in Koordinatenform
Es ist $\vec n\circ\overrightarrow{EF}=0$ und $\vec n\circ\overrightarrow{EH}=0$ .
$\overrightarrow{EH}= \overrightarrow{OH}- \overrightarrow{OE}=\begin{pmatrix}-20\\40\\120\end{pmatrix}-\begin{pmatrix}0\\40\\120\end{pmatrix}=\begin{pmatrix}-20\\0\\0\end{pmatrix}$
$\Rightarrow\;\vec n\circ\begin{pmatrix}0\\18\\-6\end{pmatrix}=0$ und $\vec n\circ\begin{pmatrix}-20\\0\\0\end{pmatrix}=0$
Man erhält zwei Gleichungen:
$18\cdot n_2-6\cdot n_3=0$ und $-20\cdot n_1=0\;\Rightarrow\;n_1=0$
$n_3$ ist frei wählbar, z.B. $n_3=3\;\Rightarrow\;18\cdot n_2-6\cdot 3=0\;\Rightarrow\;n_2=1$
Der Vektor $\vec n=\begin{pmatrix}0\\1\\3\end{pmatrix}$ .
Mit diesem Normalenvektor ist $E:\;y+3z=c$
Setze z.B. den Punkt $E(0|40| 120)$ ein, der in der Ebene liegt.
$\Rightarrow\;40+3\cdot 120=c\;\Rightarrow\;c=400$
Damit ist $E_{EFGH}:\;y+3z=400$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es ist $\vec n\circ\overrightarrow{EF}=0$ und $\vec n\circ\overrightarrow{EH}=0$ .
Man erhält zwei Gleichungen, um den Vektor $\vec n$ zu bestimmen.
Mit diesem Vektor $\vec n$ und einem Punkt, der in der Ebene liegt, kann die Ebenengleichung ermittelt werden.
Auf den Betonkörper treffendes Sonnenlicht kann im Modell durch parallele Geraden beschrieben werden. Der Richtungsvektor dieser Geraden ist $\def\arraystretch{1.25} \left(\begin{array}{c}-2 \\ 1 \\ -3\end{array}\right)$ .
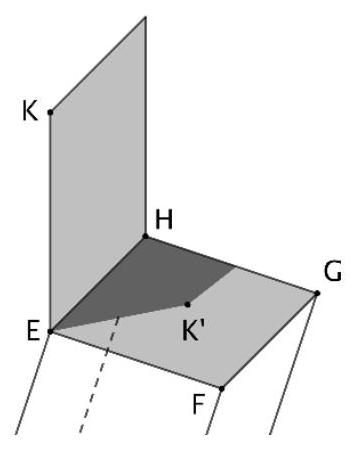
Die Karte wird so positioniert, dass sie vertikal steht (vgl. Abbildung). Durch den Eckpunkt $K$ wird ein Schattenpunkt $K^{\prime}$ auf der Deckseite des Betonkörpers erzeugt.
Ermitteln Sie die Koordinaten von $K^{\prime}$ .
(6 BE)
Mit Ausnahme der Position, die in der Teilaufgabe c) betrachtet wurde, können alle
Positionen der Karte jeweils durch eine der Ebenen $E_a:\;a \cdot y +z = 40 \cdot a +120$ mit $a\in \mathbb{R}$ beschrieben werden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
Koordinaten von $K^{\prime}$
Der Punkt $K$ hat die gleichen x- und y-Koordinaten wie der Punkt $E$ .
Die z-Koordinate von $K$ ist gleich der vom Punkt $E$ verlängert um $|\overrightarrow{EF}|$ :
$K(0|40|120+|\overrightarrow{EF}|)$
Mit $\overrightarrow{EF}=\begin{pmatrix}0\\18\\-6\end{pmatrix}$ (aus Aufgabe a)) folgt für den Betrag:
$|\overrightarrow{EF}|=\sqrt{0^2+18^2+(-6)^2}=\sqrt{360}=6\cdot \sqrt{10}$
Geradengleichung
Dann ergibt sich die Geradengleichung des Sonnenlichtes durch den Punkt $K$ mit dem gegebenen Richtungsvektor:
Wert des Parameters und Koordinaten von $K'$
Die Gerade $g$ muss mit der Ebene $E:\; y+3 \cdot z=400$ aus Aufgabe b) geschnitten werden, um den Punkt $K'$ zu erhalten:
Einsetzen von $g$ in $E$ liefert die Gleichung:
Der GTR liefert als Lösung $r\approx7{,}115124...$ .
Damit ist $r\approx7{,}12$ .
Die Koordinaten von $K'$ ergeben sich durch Einsetzen von $r\approx7{,}12$ in die Geradengleichung:
Der Punkt $K'$ hat etwa die Koordinaten $K'(-14|47|118)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Koordinaten des Punktes $K$ .
Erstelle die Geradengleichung durch den Punkt $K$ mit dem gegebenen Richtungsvektor des Sonnenlichtes.
Schneide die Gerade mit der Ebene $E_{EFGH}$ .
Setze den erhaltenen Parameter in die Geradengleichung ein, um die Koordinaten des gesuchten Punktes $K'$ zu erhalten.

Ermitteln Sie denjenigen Wert von $a$ , für den die Karte auf der Deckseite des Betonkörpers liegt. (3 BE)

Geben Sie die Bedeutung der Lösung der Gleichung $\def\arraystretch{1.25} \left(\begin{array}{c}-2 \\ 1 \\ -3\end{array}\right) \cdot\left(\begin{array}{l}0 \\ a \\ 1\end{array}\right)=0$ bezüglich der Position der Karte zum Sonnenlicht an.
Beschreiben Sie für diese Position den durch die Karte auf die Deckseite fallenden Schatten. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Bedeutung der Lösung der Gleichung
$\def\arraystretch{1.25} \left(\begin{array}{c}-2 \\ 1 \\ -3\end{array}\right) \cdot\left(\begin{array}{l}0 \\ a \\ 1\end{array}\right)=0$
Der erste Vektor ist der Richtungsvektor des Sonnenlichtes. Der zweite Vektor ist der Normalenvektor der Ebene $E_a$ . Wenn das Skalarprodukt den Wert null hat, dann stehen diese beiden Vektoren senkrecht aufeinander. Das hat zur Folge, dass die Ebene, die die Karte darstellt, parallel zum Sonnenlicht verläuft.
Beschreibung des Schattens
Da die Ebene, die die Karte darstellt, parallel zum Sonnenlicht verläuft, fällt kein Schatten von dieser Karte auf die Deckfläche des Betonkörpers.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Der erste Vektor ist der Richtungsvektor des Sonnenlichtes. Der zweite Vektor ist der Normalenvektor der Ebene $E_a$ .
Untersuche das Skalarprodukt der Vektoren.
Teil 2
Verläuft eine Ebene parallel zu den Sonnenstrahlen, dann wirft sie keinen Schatten.
Liegt die Karte auf der Deckseite des Betonkörpers, wird einer ihrer Eckpunkte durch $F$ dargestellt. Dieser Eckpunkt nimmt während des Umklappens verschiedene Positionen ein. Zwei dieser Positionen werden durch $P\left(0\left|y_{1}\right| z\right)$ und $Q\left(0\left|y_{2}\right| z\right)$ mit $y_{2}<y_{1}$ beschrieben, wobei $|\overrightarrow{F P}|=y_{1}-y_{2}$ gilt.
Begründen Sie, ohne zu rechnen, dass die Strecken $\overline{E F}$ und $\overline{E Q}$ einen doppelt so großen Winkel einschließen wie die Strecken $\overline{E F}$ und $\overline{E P}$ , und veranschaulichen Sie Ihre Begründung durch eine geeignet beschriftete Skizze. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kongruenz
Begründung, dass die Strecken $\overline{E F}$ und $\overline{E Q}$ einen doppelt so großen Winkel einschließen wie die Strecken $\overline{E F}$ und $\overline{E P}$
Zwei dieser Positionen werden durch $P\left(0\left|y_{1}\right| z\right)$ und $Q\left(0\left|y_{2}\right| z\right)$ mit $y_{2}<y_{1}$ beschrieben. Bei den beiden Punkten sind die x- und y-Koordinaten gleich groß. Somit stellt $y_2-y_1$ ihren Abstand dar. Andererseits ist $|\overrightarrow{F P}|=y_{1}-y_{2}$ .
Skizze in der y-z-Ebene:
Skizze zur Aufgabe
Welche Informationen haben wir?
Die folgenden Strecken sind gleich groß, d.h. $\overline{E F}=\overline{EP}=\overline{E Q}$ , da es sich um den Drehradius handelt.
Weiterhin sind laut Aufgabentext die Strecken $\overline{PQ}=\overline{FP}$ .
Damit sind die beiden Dreiecke $EFP$ und $EPQ$ zueinander kongruent und liegen bzgl. der Strecke $\overline{EP}$ achsensymmetrisch zueinander.
Der Winkel im Viereck $EFPQ$ im Eckpunkt $E$ ist somit doppelt so groß, wie der eines der Dreiecke im Eckpunkt $E$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Weise nach, dass die beiden Dreiecke $EFP$ und $EPQ$ zueinander kongruent sind.

$\displaystyle a\cdot 58+114$	$=$	$\displaystyle 40\cdot a+120$	$\displaystyle -40\cdot a$
	↓	Löse nach $a$ auf.
$\displaystyle 18\cdot a+114$	$=$	$\displaystyle 120$	$\displaystyle -114$
$\displaystyle 18\cdot a$	$=$	$\displaystyle 6$	$\displaystyle :18$
$\displaystyle a$	$=$	$\displaystyle \dfrac{1}{3}$

Aufgabe 3C

Zeigen Sie, dass die Kanten AE‾\overline{A E}AE und BF‾\overline{B F}BF parallel sind

Hat das Viereck ABFEABFEABFE im Punkt EEE einen rechten Winkel?

Hast du eine Frage oder Feedback?

Gleichung der Ebene, in der das Rechteck EFGHE F G HEFGH liegt, in Koordinatenform

Hast du eine Frage oder Feedback?

Koordinaten von K′K^{\prime}K′

Geradengleichung

Wert des Parameters und Koordinaten von K′K'K′

Hast du eine Frage oder Feedback?

Wert von aaa, für den die Karte auf der Deckseite des Betonkörpers liegt

Hast du eine Frage oder Feedback?

Bedeutung der Lösung der Gleichung

Beschreibung des Schattens

Hast du eine Frage oder Feedback?

Begründung, dass die Strecken EF‾\overline{E F}EF und EQ‾\overline{E Q}EQ​ einen doppelt so großen Winkel einschließen wie die Strecken EF‾\overline{E F}EF und EP‾\overline{E P}EP

Hast du eine Frage oder Feedback?

Zeigen Sie, dass die Kanten $\overline{A E}$ und $\overline{B F}$ parallel sind

Hat das Viereck $ABFE$ im Punkt $E$ einen rechten Winkel?

Gleichung der Ebene, in der das Rechteck $E F G H$ liegt, in Koordinatenform

Koordinaten von $K^{\prime}$

Wert des Parameters und Koordinaten von $K'$

Wert von $a$ , für den die Karte auf der Deckseite des Betonkörpers liegt

Begründung, dass die Strecken $\overline{E F}$ und $\overline{E Q}$ einen doppelt so großen Winkel einschließen wie die Strecken $\overline{E F}$ und $\overline{E P}$