Wahlteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben des Teil 2 mit Wahlteil (ab S. 7) der Realschulprüfung 2022. Zum Download hier.

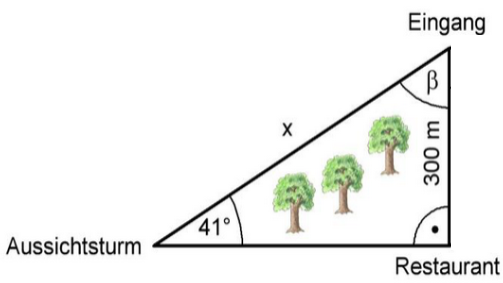
Wahlaufgabe 1 - Trigonometrie

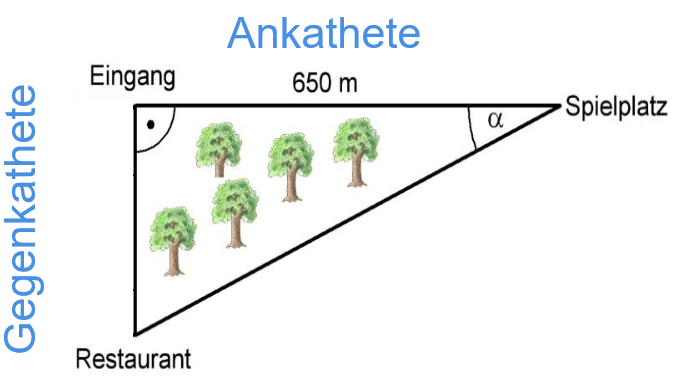
Die Abbildung zeigt den Übersichtsplan eines Stadtparks.

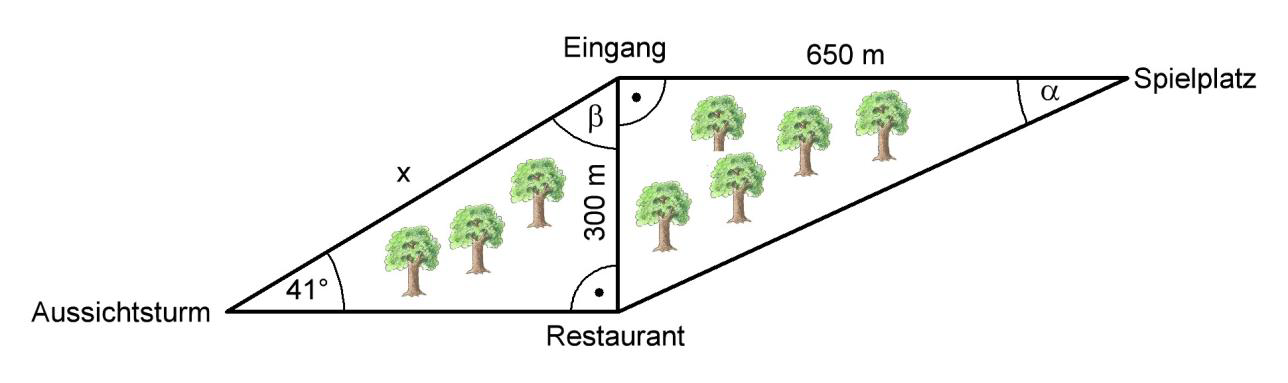
Quelle: MK Niedersachsen (Skizze nicht maßstäblich) — Quelle: MK Niedersachsen
(Skizze nicht maßstäblich)

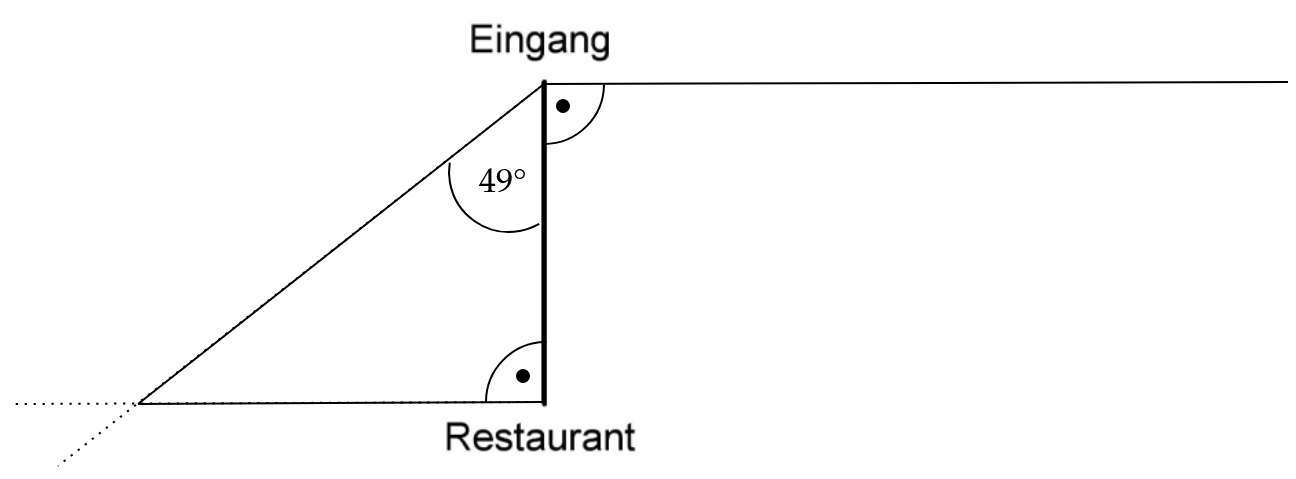
Anna behauptet, dass der Winkel $β = 49°$ beträgt.

Zeige mithilfe einer Rechnung, dass Anna recht hat. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkelsumme im Dreieck
Das Dreieck hat drei Winkel mit den Größen:
$41°$
$90°$
$\beta$
Da die Winkelsumme $180°$ beträgt, gilt:
$\displaystyle 41°+90°+\beta$ $=$ $\displaystyle 180°$ $\displaystyle -41°-90°$
$\displaystyle \beta$ $=$ $\displaystyle 49°$
Anne hat recht, der Winkel $\beta$ ist $49°$ groß.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme das Dreieck, in dem $\beta$ liegt.
Die Winkelsumme in einem Dreieck beträgt immer $180°$ .
Verwende die Winkelsumme, um $\beta$ zu berechnen.
Anna beginnt mit der maßstäblichen Zeichnung des Übersichtsplans.
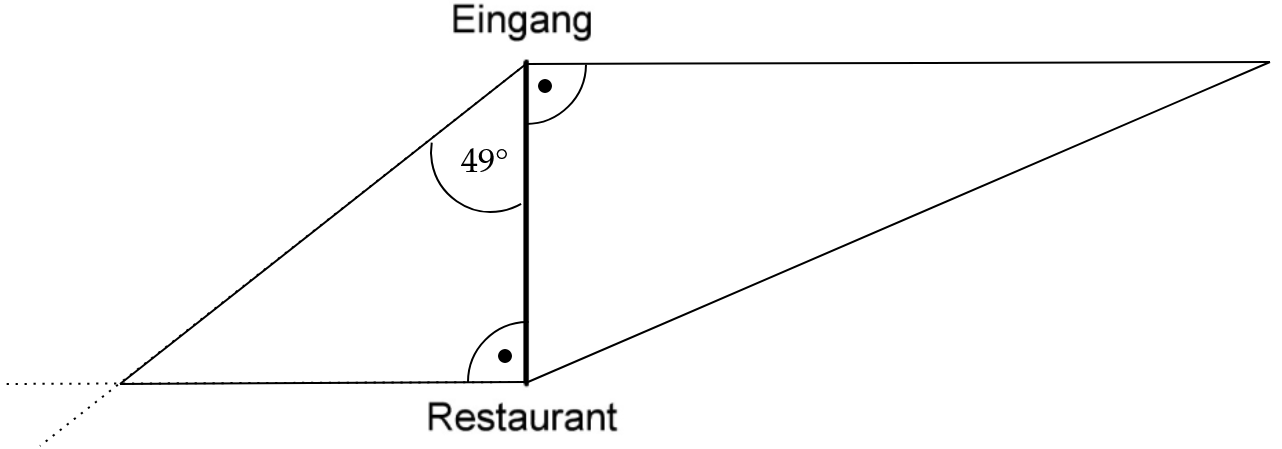
Vervollständige Annas Zeichnung. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lot zeichnen
Skizziere eine Hilfslinie, die am Eingang im Winkel $49°$ zur Strecke steht.
Hilfslinie
Die zweite Hilfslinie steht senkrecht auf der Strecke.
Sie schneidet die erste Hilfslinie, sodass sie zusammen das linke Dreieck bilden.
Senkrechte
Linkes Dreieck
Auf der anderen Seite muss ein Lot am Eingang eingezeichnet werden.
Die Länge dieses Lots muss im richtigen Verhältnis zur Strecke "Eingang-Restaurant" stehen.
Lot
Im letzten Schritt müssen die Enden der Strecken nur noch fertig verbunden werden.
Fertige Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Skizziere eine Hilfslinie, die am Eingang im $49°$ -Winkel zur Strecke steht.
Zeichne beim Restaurant das Lot zur Strecke ein, sodass sich ein Schnittpunkt mit der Hilfslinie bildet.
Zeichne ein weiteres Lot ein, welches vom Eingang aus nach rechts geht. Die Länge der Strecke oben rechts muss im richtigen Maßstab zur ursprünglichen Strecke stehen.
Verbinde das Ende des Lots und das Ende der Strecke beim Restaurant.
Kreuze den Maßstab an, den Anna wählte. (1 BE)
- 1 : 100
- 1 : 1000
- 1 : 10 000
Für diese Aufgabe benötigst Du folgendes Grundwissen: Maßstab berechnen
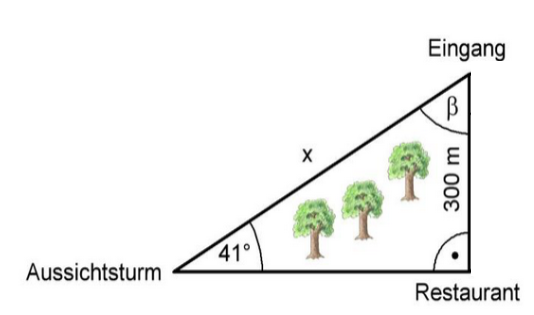
Die Strecke "Eingang-Restaurant" ist laut Skizze $300~m$ lang.
Auf dem Papier misst die Strecke: $3~cm=0{,}03~m$
Das entspricht einem Maßstab von:
$\displaystyle 300:0{,}03$
↓
Dividiere
$=$ $\displaystyle 10000$
Der verwendete Maßstab ist $1:10000$ . Achte darauf, dass die Längen unterschiedliche Einheiten besitzen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Dividiere die Länge, die in der Skizze angegeben ist, durch die tatsächliche Länge auf dem Papier.
Das sollte mit jeder Strecke funktionieren.

Berechne die Größe des Winkels $\alpha$ . (2 BE)

Berechne die Länge der Strecke $x$ . (3 BE)

Wahlaufgabe 2 - Körper

Der abgebildete Schokokuss besteht annähernd aus zwei geometrischen Teilkörpern.
Kreuze diese beiden Teilkörper an. (1 BE)
- Pyramide
- Kegel
- Kugel
- Halbkugel
- Zylinder
- Quader
Der Körper ist aus einem Zylinder und einer Halbkugel zusammengesetzt.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist hilfreich, den Schokokuss von verschiedenen Seiten anzusehen:
Von oben scheint der Schokokuss ein kreisförmiger Körper zu sein.
Von der Seite ist die Figur aus einem Rechteck und einem Halbkreis zusammengesetzt.
Die Abbildung zeigt den Querschnitt eines Schokokusses.
Ein Hersteller bietet Schokoküsse in einem quaderförmigen Karton an. Der Karton ist 20 cm lang, 16 cm breit und 19 cm hoch.
Bestimme die maximale Anzahl der Schokoküsse, die in diesem Karton verpackt sind. (2 BE)
Wir gehen davon aus, dass der beste Weg, die Schokoküsse zu stapeln, folgender ist:
Die Schokoküsse werden in Reihen gestellt und aufrecht aufeinander gestapelt.
Sie werden nicht schräg oder versetzt gestapelt. Das würde es sehr kompliziert machen.
Skizze des Kartons
Lange Seite des Kartons
In die lange Seite des Kartons kann man $20:3{,}8\approx5{,}26$ Schokoküsse stellen.
Das macht $5$ ganze Schokoküsse.
Lange Seite
Kurze Seite des Kartons
In die kurze Seite des Kartons kann man $16:3{,}8\approx 4{,}21$ Schokoküsse stellen.
Das macht $4$ ganze Schokoküsse.
Kurze Seite
Höhe des Kartons
Es passen $19:6{,}2\approx 3{,}06$ Schokoküsse aufeinander in den Karton.
Das sind $3$ ganze Schokoküsse.
Höhe
Gesamtanzahl
Insgesamt passen $5\cdot 4\cdot 3=60$ Schokoküsse in den Karton.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Anzahl der Schokoküsse, die in die lange Seite passen.
Bestimme die Anzahl der Schokoküsse, die auf die kurze Seite passen.
Bestimme die Anzahl der Schokoküsse, die in die Höhe des Kartons gestapelt passen.
Multipliziere diese drei Werte miteinander.

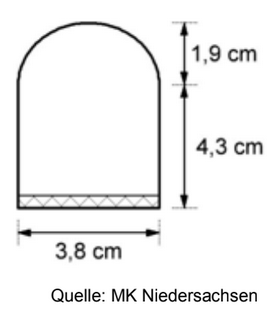
Berechne das Volumen eines Schokokusses. (5 BE)

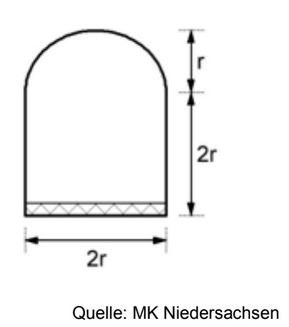
In der Grafik ist ein anderer Schokokuss abgebildet.

Stelle eine allgemeine Formel auf, mit der du das Volumen in Abhängigkeit von r berechnen kannst. (2 BE)

3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Wahlaufgabe 3 - Wachstumsprozesse
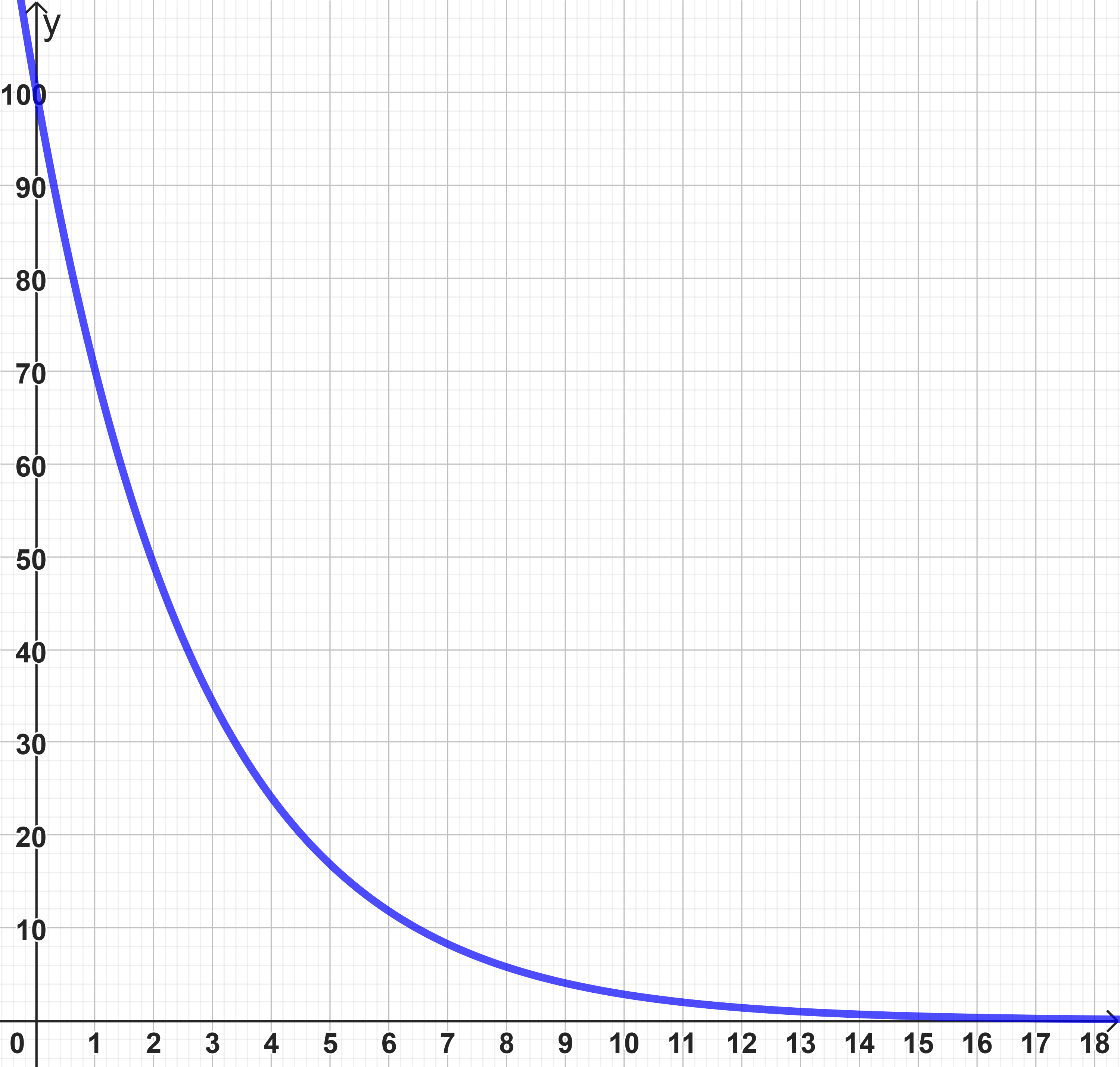
Um eine Bauchspeicheldrüse zu untersuchen, wird dem Patienten ein Farbstoff gespritzt.
Eine gesunde Bauchspeicheldrüse scheidet pro 10 Minuten ca. 30 % des jeweils noch vorhandenen Farbstoffes aus.
1. Vervollständige die Tabelle. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Änderungsrate
  Alle 10 Minuten gehen $30~\%$ verloren. Das heißt, es bleiben nur $70~\%$ übrig. Das ist die Änderungsrate des exponentiellen Zerfalls.
  Fehlenden Wert berechnen
  Der fehlende Wert ergibt sich durch: $70\cdot 0{,}7=49$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Faktor (Änderungsrate), um den sich die Konzentration alle 10 Minuten verringert.
  Berechne den fehlenden Wert, indem $70$ mit der Änderungsrate multipliziert wird.
2. Zeichne die Wertepaare in ein Koordinatensystem und verbinde sie sinnvoll. Wähle für die x-Achse 1 cm für 10 Minuten und für die y-Achse 1 cm für 10 %. (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Lösung
  Lösung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zeichne ein Koordinatensystem.
  Die x-Achse gibt die Zeit an. 1cm entspricht 10 Minuten.
  Die y-Achse gibt die Farbstoffmenge in % an. 1cm entspricht 10%.
  Trage alle Werte ein.
  Verbinde die Werte so, dass eine durchgehende Kurve ohne Ecken entsteht.
3. Kreuze die Art der Zuordnung an. (1 BE)
  linear
  quadratisch
  exponentiell
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Es liegt exponentieller Zerfall vor.
  Begründung: "10 Minuten" und "Farbstoffmenge" hängen durch eine konstante Änderungsrate zusammen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Gib die Farbstoffmenge in % nach 25 Minuten an. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Mit der Skizze aus Teilaufgabe (b) kann der Wert bei $x=2{,}5$ abgelesen werden.
  Die Farbstoffmenge liegt bei etwa:
  Skizze aus Teilaufgabe (b)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Wert durch die Skizze aus Teilaufgabe (b).
  Lies den Funktionswert bei $x=2{,}5$ ab.
5. Gib an, nach welcher Zeit noch 10 % des Farbstoffes vorhanden sind. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Mit der Skizze aus Teilaufgabe (b) kann der Wert bei $y=10~\%$ abgelesen werden.
  Nach etwa $65$ Minuten sind noch $10~\%$ der Farbstoffmenge übrig.
  Skizze aus Teilaufgabe (b)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Wert durch die Skizze aus Teilaufgabe (b).
  Schaue nach, bei welchem x-Wert der Funktionswert (y-Achse) 10 % beträgt.
6. Einem Patienten werden 0,2 g Farbstoff gespritzt. Nach 20 Minuten sind noch 0,1 g des Farbstoffes in der Bauchspeicheldrüse vorhanden.
  Entscheide, ob der Patient eine gesunde Bauchspeicheldrüse hat. Begründe deine Entscheidung. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
  Nach 20 Minuten sind mit der Änderungsrate $0{,}7$ noch
  $0{,}2\cdot 0{,}7^2=0{,}098$
  Gramm des Farbstoffs übrig.
  Das stimmt näherungsweise mit dem Wert des Patienten überein.
  Der Patient hat eine gesunde Bauchspeicheldrüse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne, wie viel Farbstoff nach 20 Minuten mit der Änderungsrate $0{,}7$ übrig wäre.
  Vergleiche den Wert mit dem des Patienten.

Wahlaufgabe 4 - Quadratische Funktionen

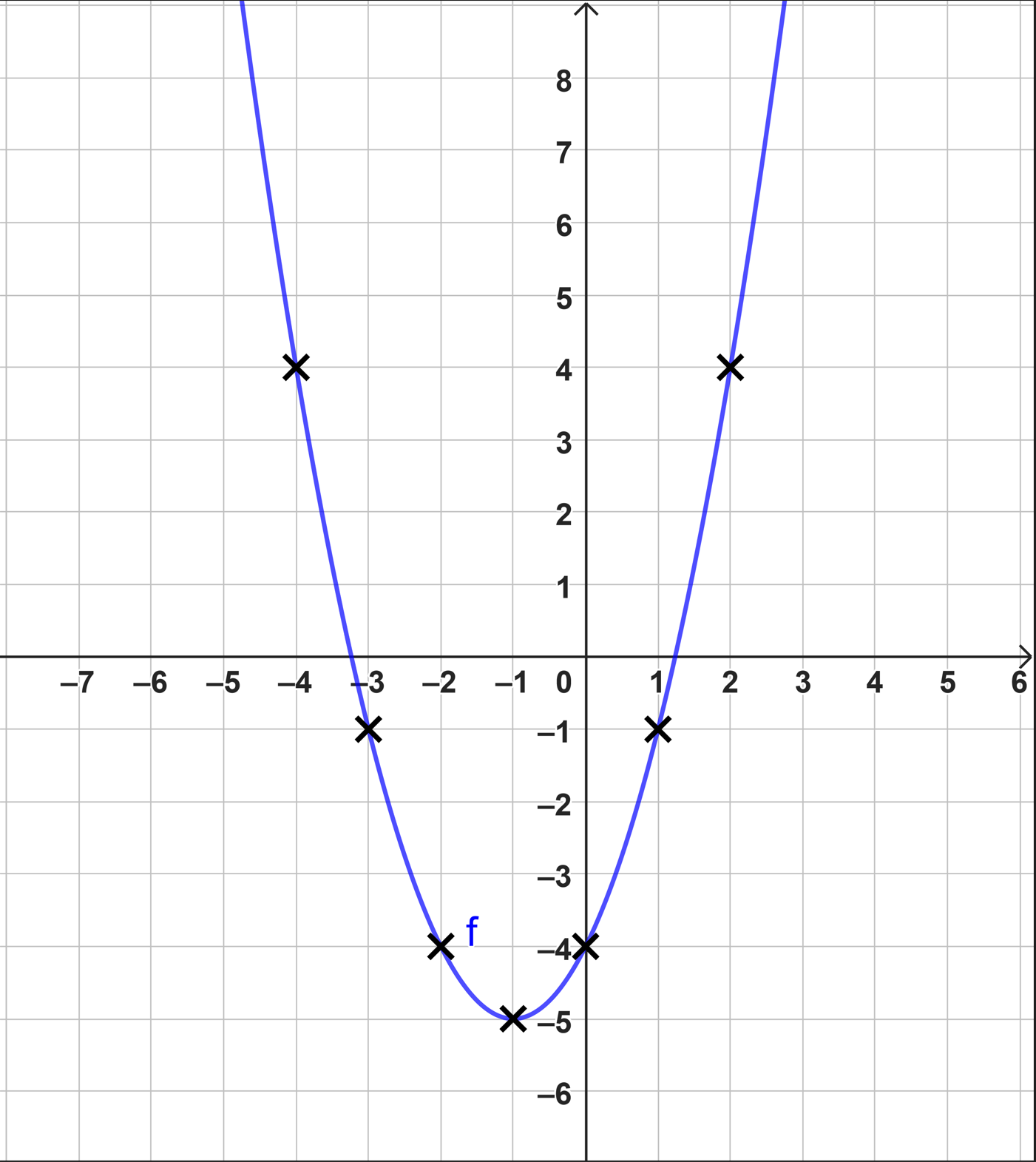
Die Abbildung zeigt vier Graphen von quadratischen Funktionen.

Ordne die Graphen den passenden Funktionsgleichungen zu. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm einer Parabel
Die richtige Zuordnung ist:
Lösung
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vergleiche die Scheitel der Parabel im Koordinatensystem mit den Scheiteln aus den Scheitelpunktformen.
Verwende, dass Parabeln der Form $y=ax^2+c$ auf der y-Achse liegen.

Eine andere quadratische Funktion hat die Funktionsgleichung $y = x^2 + 2x − 4.$

Vervollständige die Wertetabelle und zeichne den Graphen der Funktion in ein

Koordinatensystem. (3 BE)

Gib die Koordinaten des Scheitelpunktes der Funktion an. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
Der Scheitel ist der Punkt:
$S(-1|-5)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Verwende die Skizze aus Aufgabenteil (c).
Lies den Scheitelpunkt im Koordinatensystem ab.
Hinweis: Der Scheitel ist der tiefste bzw. höchste Punkt einer Parabel.

Berechne die Nullstellen der Funktion $y = x^2 + 2x − 4$ . (3 BE)

Verändere die Funktionsgleichung $y = x^2 + 2x − 4$ so, dass der Graph keine Nullstelle hat. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
In der Berechnung der Nullstelle kam es zum Term: $\sqrt{\left(\frac{2}{2}\right)^2-\underbrace{\left(-4\right)}_{q}}$
Wenn unter dieser Wurzel eine negative Zahl steht, hat die Parabel keine Nullstelle.
Jeder Wert $q>1$ macht den Wert unter der Wurzel negativ. Ein Beispiel wäre also $q=2$ (ein möglicher Wert reicht).
$y=x^2+4x+2$ wäre eine mögliche Lösung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gib einen Wert für $q$ an, sodass die $pq$ -Formel keine Lösung hat.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \tan\alpha$	$=$	$\displaystyle \frac{Gegenkathete}{Ankathete}$
	↓	Einsetzen der Längen
	$=$	$\displaystyle \frac{300}{650}$	$\displaystyle \tan^{-1}$
	↓	$\tan^{-1}$ verwenden, um nach $\alpha$ umzustellen
$\displaystyle \alpha$	$=$	$\displaystyle \tan^{-1}\left(\frac{300}{650}\right)$
	$=$	$\displaystyle 24{,}775...°$
	↓	Runden
	$≈$	$\displaystyle 24{,}78°$

$\displaystyle \sin41°$	$=$	$\displaystyle \frac{300}{x}$	$\displaystyle \cdot x$
$\displaystyle \sin41^°\cdot x$	$=$	$\displaystyle 300$	$\displaystyle :\sin41°$
$\displaystyle x$	$=$	$\displaystyle \frac{300}{\sin41°}$
$\displaystyle x$	$=$	$\displaystyle 457{,}275...$
	$≈$	$\displaystyle 457{,}28$

$\displaystyle V$	$=$	$\displaystyle \pi r^2\cdot h$
	↓	Einsetzen
	$=$	$\displaystyle \pi\cdot1{,}9^2\cdot4{,}3$
	$=$	$\displaystyle 48{,}766...$
	$≈$	$\displaystyle 48{,}77$

$\displaystyle V$	$=$	$\displaystyle \frac{\frac{4}{3}\pi\cdot r^3}{2}$
	$=$	$\displaystyle \frac{2}{3}\pi\cdot r^3$
	↓	Einsetzen
	$=$	$\displaystyle \frac{2}{3}\pi\cdot1{,}9^3$
	$=$	$\displaystyle 14{,}365...$
	$≈$	$\displaystyle 14{,}37$

$\displaystyle V$	$=$	$\displaystyle \pi\cdot r^2\cdot h$
	↓	$h=2r$ einsetzen
	$=$	$\displaystyle \pi\cdot r^2\cdot2r$
	↓	Zusammenfassen
	$=$	$\displaystyle 2\pi\cdot r^3$

Wahlteil

Wahlaufgabe 1 - Trigonometrie

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahlaufgabe 2 - Körper

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Volumen der Halbkugel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahlaufgabe 3 - Wachstumsprozesse

Änderungsrate

Fehlenden Wert berechnen

Hast du eine Frage oder Feedback?

Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahlaufgabe 4 - Quadratische Funktionen

Hast du eine Frage oder Feedback?

y-Wert

Wertetabelle

Skizze der Parabel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$\displaystyle 41°+90°+\beta$	$=$	$\displaystyle 180°$	$\displaystyle -41°-90°$
$\displaystyle \beta$	$=$	$\displaystyle 49°$

	$\displaystyle 300:0{,}03$
	↓ Dividiere
$=$	$\displaystyle 10000$

$\displaystyle V_{ges}$	$=$	$\displaystyle 2\pi\cdot r^3+\frac{2}{3}\pi\cdot r^3$
	$=$	$\displaystyle \frac{8}{3}\pi\cdot r^3$

$\displaystyle y$	$=$	$\displaystyle x^2+2x-4$
	↓	$x=-2$ einsetzen
	$=$	$\displaystyle \left(-2\right)^2-2\cdot2-4$
	↓	$(-2)^2=4$
	$=$	$\displaystyle 4-4-4$
	$=$	$\displaystyle -4$

$\displaystyle 0$	$=$	$\displaystyle x^2+2x-4$
	↓	$p=2,~q=-4$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle -\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$
	↓	$p$ und $q$ einsetzen
	$=$	$\displaystyle -\frac{2}{2}\pm\sqrt{\left(\frac{2}{2}\right)^2-\left(-4\right)}$
	$=$	$\displaystyle -1\pm\sqrt{1+4}$
	$=$	$\displaystyle -1\pm\sqrt{5}$
$\displaystyle \Rightarrow\ x_1$	$=$	$\displaystyle -1+\sqrt{5}$
$\displaystyle \Rightarrow\ x_2$	$=$	$\displaystyle -1-\sqrt{5}$