Pflichtteil - Stochastik

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgabe P1

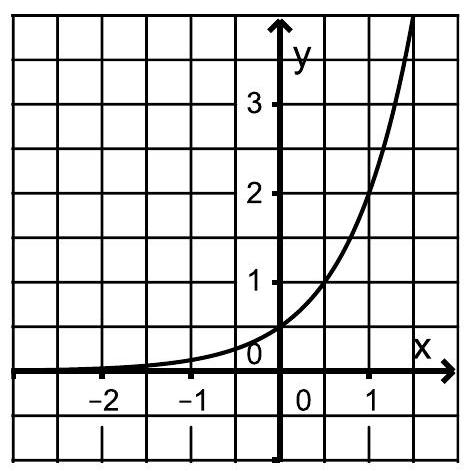
Die Abbildung zeigt den Graphen der

Funktion $f$ mit $f(x)=a \cdot b^{x}$ mit $a>0$ und $b>0$ .

Bestimmen Sie die passenden Werte von $a$ und $b$ . (3 BE)

Der Graph der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=3^{x}$ wird um 2 in negative $x$ -Richtung verschoben.
Zeigen Sie, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von $g$ in $y$ -Richtung erzeugt werden kann. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
Verschiebung um $2$ in negativer $x$ -Richtung
$g(x)=3^{x+2}$
Umformung von $g(x)$
$g(x)=3^{x+2}= 3^x\cdot3^2=9\cdot3^x$
Somit kann $g(x)$ auch durch eine Streckung in $y$ -Richtung um den Faktor $9$ erzeugt werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Ersetze $x$ durch den Term $x+2$ in der Funktionsgleichung.
Wende die Potenzgesetze an.

Aufgabe P2

Eine ganzrationale Funktion $f$ hat die Nullstellen 1, 2 und -3.
Geben Sie eine Funktionsgleichung für $f$ an. (2 BE)

Funktionsgleichung
Setze die Nullstellen in die Nullstellenform/Linearform ein:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle den Funktionsterm in der Nullstellenform/Linearform auf: $f(x)=(x-n_1)\cdot(x-n_2)...$

Für eine Funktion $h$ gilt: $h^{\prime}(x)=x^{2}-2 x-24$

Bestimmen Sie die Extremstellen des Graphen von $h$ . (3 BE)

Aufgabe P3

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^{2}$ .

Bestimmen Sie diejenige reelle Zahl $m$ mit $m<0$ , für die der Graph von $f$ und die Gerade mit der Gleichung $y=m \cdot x$ eine Fläche mit dem Inhalt 36 einschließen. (5 BE)

4
Aufgabe P4
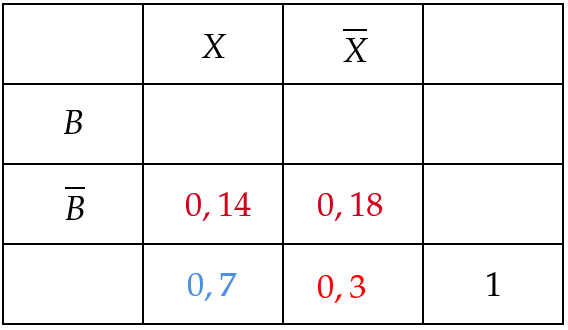
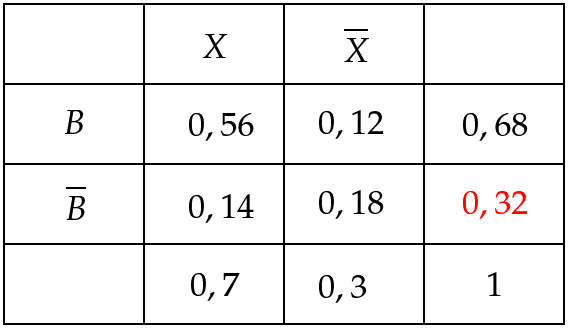
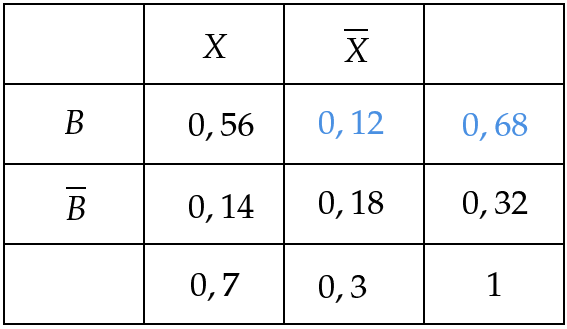
In einer Gemeinde gab es beim Streit um ein neues Bauprojekt eine Befragung. Von den Teilnehmenden waren $70 \%$ älter als 35 Jahre. $60 \%$ der höchstens 35-Jährigen und $20 \%$ der über 35-Jährigen, die an der Befragung teilnahmen, stimmten gegen das Bauprojekt.
1. Bestimmen Sie das Ergebnis der Befragung. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
  Ergebnis der Befragung
  $X$ steht für: Person ist über 35 Jahre alt
  $B$ steht für: Person stimmt für das Bauprojekt
  Aus der Aufgabenstellung ergeben sich bereits folgende Werte in der Vierfeldertafel:
  Der Anteil der über 35-jährigen Personen ist $0{,}7$ .
  Damit ist der Anteil der höchstens 35-jährigen Personen $0{,}3$ .
  $60~\%$ der höchstens 35-Jährigen entsprechen $0{,}3\cdot0{,}6=0{,}18$ .
  $20~\%$ der über 35-Jährigen entsprechen $0{,}2\cdot 0{,}7=0{,}14$ .
  Damit kann die Vierfeldertafel komplett ausgefüllt werden.
  Der Anteil der Personen, die gegen das Bauprojekt stimmen, steht bei $\bar{B}$ :
  $32~\%$ der Personen sind gegen das Bauprojekt.
  Damit ist das Ergebnis der Befragung, dass die Mehrheit der Personen das Bauprojekt möchten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lege eine Vierfeldertafel an mit den Variablen:
  $X$ steht für "Person ist über 35 Jahre alt"
  $B$ steht für "Person stimmt für das Bauprojekt"
  Vervollständige die Vierfeldertafel und bestimme den Anteil der Personen bei $\bar{B}$ .
2. Bestimmen Sie unter den Teilnehmenden, die für das Projekt stimmten, den Anteil der höchstens 35-Jährigen. (2 BE)
  
  Anteil bestimmen
  Der Anteil der Personen, die höchstens $35$ Jahre alt sind und für das Bauprojekt stimmen ist: $0{,}12$
  Der Anteil der Personen, die für das Bauprojekt stimmen, ist: $0{,}68$
  Insgesamt ist der Anteil also: $\dfrac{0{,}12}{0{,}68}\approx 17{,}65~\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Anteil der Personen, die höchstens 35 Jahre alt sind und für das Projekt stimmen.
  Bilde das Verhältnis zur Anzahl der Personen, die für das Projekt stimmen.
  Verwende die Vierfeldertafel aus Teilaufgabe (a).

Aufgabe P5

Für ein Zufallsexperiment wird eine Zufallsgröße $X$ festgelegt, welche die drei Werte $2$ , $5$ und $8$ annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von $X$ dargestellt.

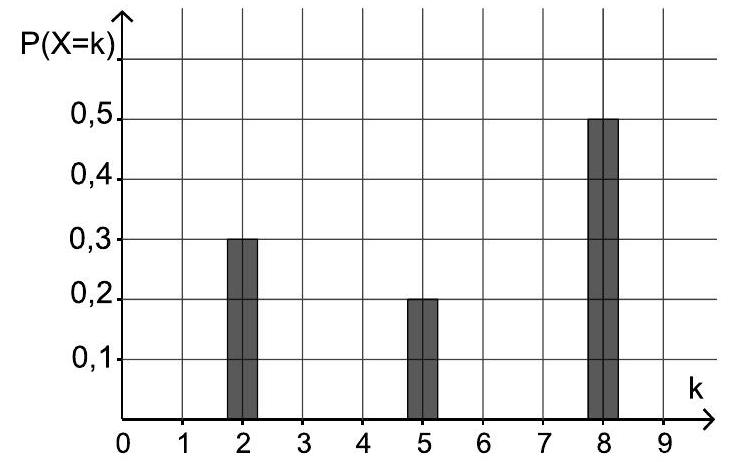
$k$	2	5	8
$P(X = k)$		$0{,}2$

Geben Sie die in der Tabelle fehlenden Werte an.

Berechnen Sie den Erwartungswert von $X$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert

Erwartungswert berechnen

Ergänze die fehlenden Werte:

$k$	2	5	8
$P(X = k)$	$0{,}3$	$0{,}2$	$0{,}5$

Der Erwartungswert beträgt:

$\displaystyle E[X]$	$=$	$\displaystyle 2\cdot P(X=2)+5\cdot P(X=5)+8\cdot P(X=8)$
	↓	Einsetzen
	$=$	$\displaystyle 2\cdot0{,}3+5\cdot0{,}2+8\cdot0{,}5$
	↓	Berechnen
	$=$	$\displaystyle 5{,}6$

Der Erwartungswert beträgt $5{,}6$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Das Zufallsexperiment wird zweimal unter gleichen Bedingungen durchgeführt.

Dabei wird jeweils der Wert der Zufallsgröße $X$ notiert.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass das Produkt dieser beiden Werte

den Wert $10$ ergibt. (2 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle f(x)$	$=$	$\displaystyle 0{,}5\cdot b^x$
	↓	Punkt einsetzen
$\displaystyle 2$	$=$	$\displaystyle 0{,}5\cdot b^1$	$\displaystyle :0{,}5$
$\displaystyle 4$	$=$	$\displaystyle b$

$\displaystyle x^2-2x-24$	$=$	$\displaystyle 0$
	↓	$pq-Formel$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle -\frac{\left(-2\right)}{2}\pm\sqrt{\left(\frac{\left(-2\right)}{2}\right)^2-\left(-24\right)}$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle 1\pm\sqrt{\left(1\right)^2+24}$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle 1\pm\sqrt{25}$

$\displaystyle mx$	$=$	$\displaystyle x^2$
$\displaystyle 0$	$=$	$\displaystyle x^2-mx$
	$=$	$\displaystyle x\left(x-m\right)$

"obere Funktion minus untere Funktion"
	↓
$\displaystyle A$	$=$	$\displaystyle \int_m^0mx-x^2dx$
	↓	Stammfunktion bilden
	$=$	$\displaystyle \left[\frac{m}{2}x^2-\frac{1}{3}x^3\right]_m^0$
	↓	Grenzen einsetzen
	$=$	$\displaystyle 0-(\frac{m^3}{2}-\frac{m^3}{3})$
	$=$	$\displaystyle -\frac{m^3}{6}$

Pflichtteil - Stochastik

Aufgabe P1

Anfangswert $a$

Wachstumsrate $b$

Hast du eine Frage oder Feedback?

Verschiebung um $2$ in negativer $x$ -Richtung

Umformung von $g(x)$

Hast du eine Frage oder Feedback?

Aufgabe P2

Funktionsgleichung

Hast du eine Frage oder Feedback?

Ableitung gleich 0 setzen und Gleichung lösen

$2$ . Ableitung

Hinreichende Bedingung

Hast du eine Frage oder Feedback?

Aufgabe P3

Schnittpunkte berechnen

Fläche berechnen

Aufgabe P4

Ergebnis der Befragung

Hast du eine Frage oder Feedback?

Anteil bestimmen

Hast du eine Frage oder Feedback?

Aufgabe P5

Erwartungswert berechnen

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit berechnen

Hast du eine Frage oder Feedback?

$\displaystyle P\left(X_1\cdot X_2=10\right)$	$=$	$\displaystyle P(X=2)\cdot P(X=5)+P(X=5)\cdot P(X=2)$
	↓	Einsetzen
	$=$	$\displaystyle 0{,}3\cdot0{,}2+0{,}2\cdot0{,}3$
	$=$	$\displaystyle 0{,}12$

Pflichtteil - Stochastik

Aufgabe P1

Anfangswert aaa

Wachstumsrate bbb

Hast du eine Frage oder Feedback?

Verschiebung um 222 in negativer xxx-Richtung

Umformung von g(x)g(x)g(x)

Hast du eine Frage oder Feedback?

Aufgabe P2

Funktionsgleichung

Hast du eine Frage oder Feedback?

Ableitung gleich 0 setzen und Gleichung lösen

222. Ableitung

Hinreichende Bedingung

Hast du eine Frage oder Feedback?

Aufgabe P3

Schnittpunkte berechnen

Fläche berechnen

Aufgabe P4

Ergebnis der Befragung

Hast du eine Frage oder Feedback?

Anteil bestimmen

Hast du eine Frage oder Feedback?

Aufgabe P5

Erwartungswert berechnen

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit berechnen

Hast du eine Frage oder Feedback?

Anfangswert $a$

Wachstumsrate $b$

Verschiebung um $2$ in negativer $x$ -Richtung

Umformung von $g(x)$

$2$ . Ableitung