Hilfsmittelfreier Teil
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Aufgaben zu Prüfung IGS E 2022, Hilfsmittelfreier Teil. Zum Download hier.
- 1
Aufgabe 1
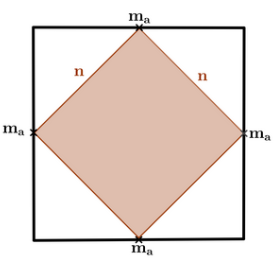
In der Abbildung siehst du einen Würfel mit einer Kantenlänge von .
In der Grundfläche werden die Mittelpunkte der Kanten zu einem Quadrat verbunden. Die Länge der Seite beträgt .
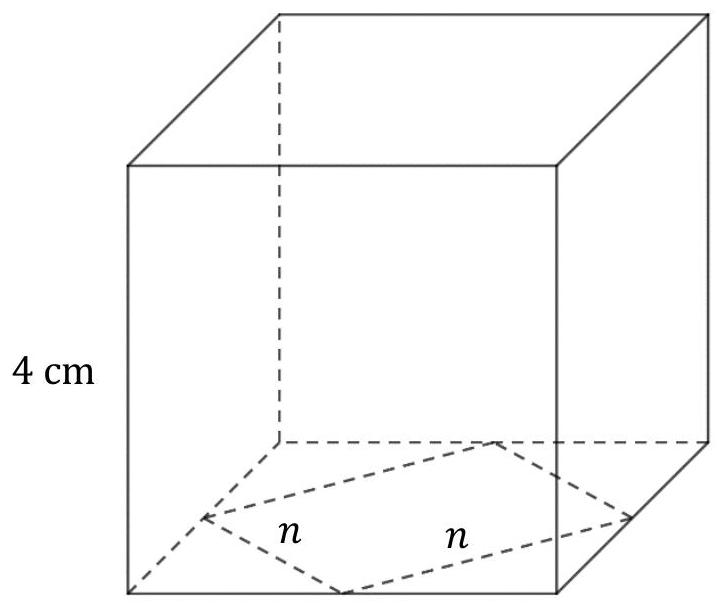
Skizze nicht maßstabsgerecht
Berechne das Volumen des Würfels. (1 BE)
Zeige durch eine Rechnung, dass die Länge der Seite tatsächlich beträgt. (2 BE)
Das Quadrat mit den Seitenlängen wird zu einem Quader erweitert.
Berechne das Volumen dieses Quaders. (2 BE)
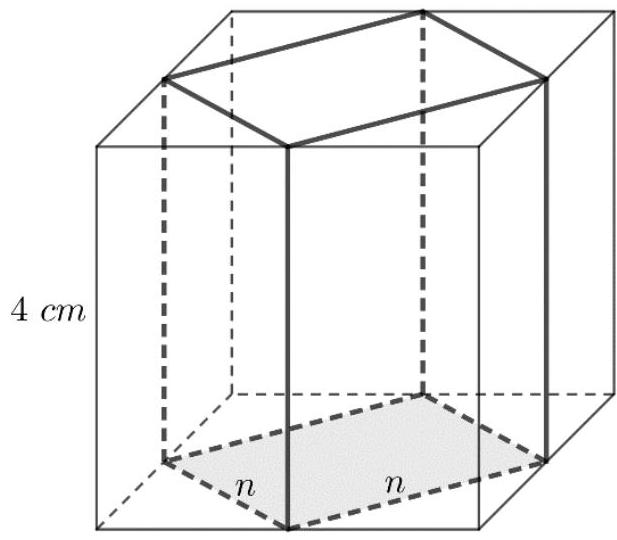
Skizze nicht maßstabsgerecht

Begründe, dass Dirk Recht hat. (2 BE)
- 2
Aufgabe 2
Du hast die Wahl zwischen zwei Zufallsversuchen.
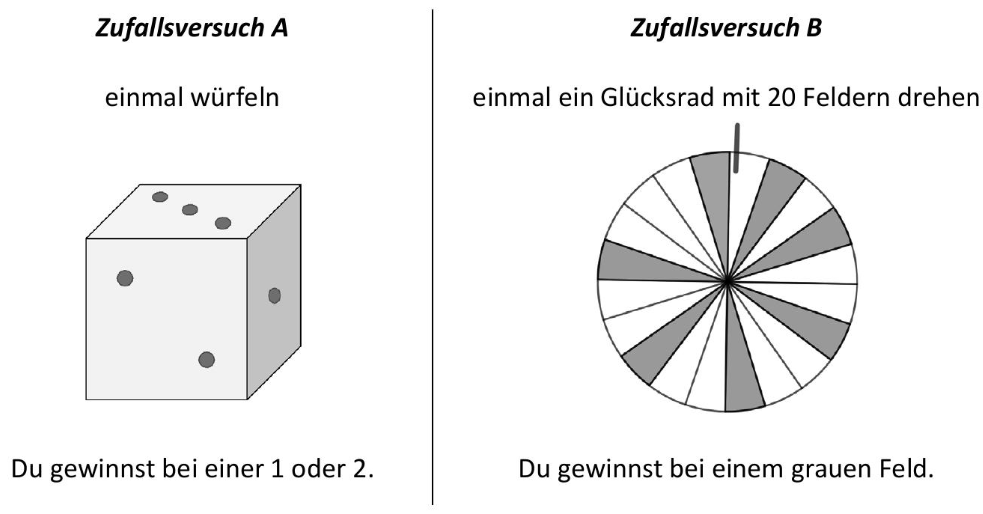
Entscheide mithilfe von Rechnungen, bei welchem Zufallsversuch die Wahrscheinlichkeit zu gewinnen größer ist. (2 BE)
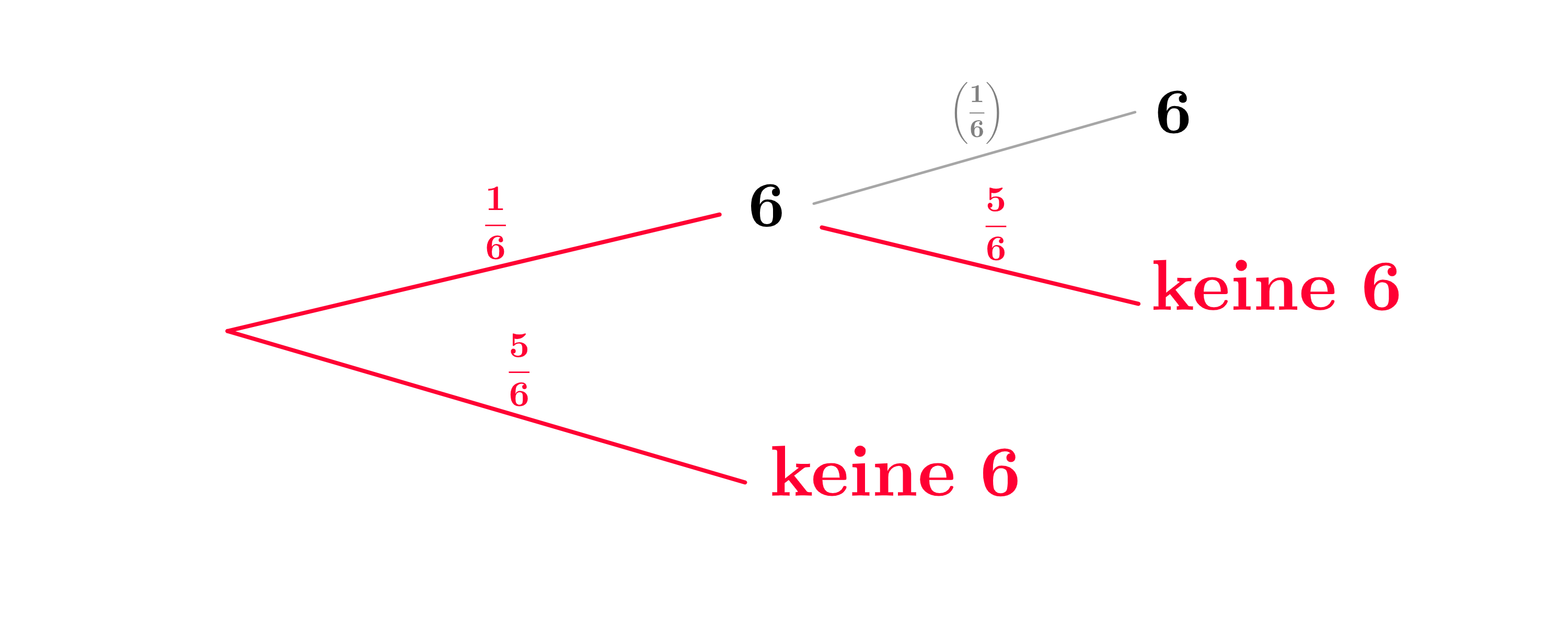
Ein Spielwürfel wird zweimal gewürfelt.
Es soll die Wahrscheinlichkeit für zweimal eine Sechs berechnet werden.
Kreuze alle Terme an, mit denen berechnet werden kann.
Erkläre, warum deine angekreuzten Terme richtig sind. (3 BE)

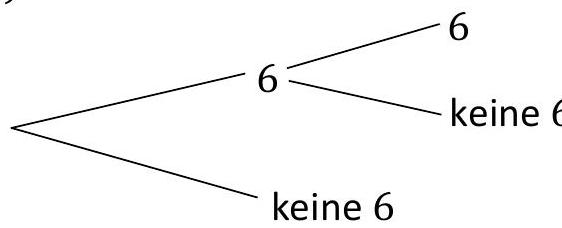
Dorothee zeichnet ein verkürztes Baumdiagramm und stellt einen Term zur Berechnung von auf:
Erkläre, warum Dorothees Term auch richtig ist. (1 BE)
- 3
Aufgabe 3
Hier siehst du verschiedene Graphen.
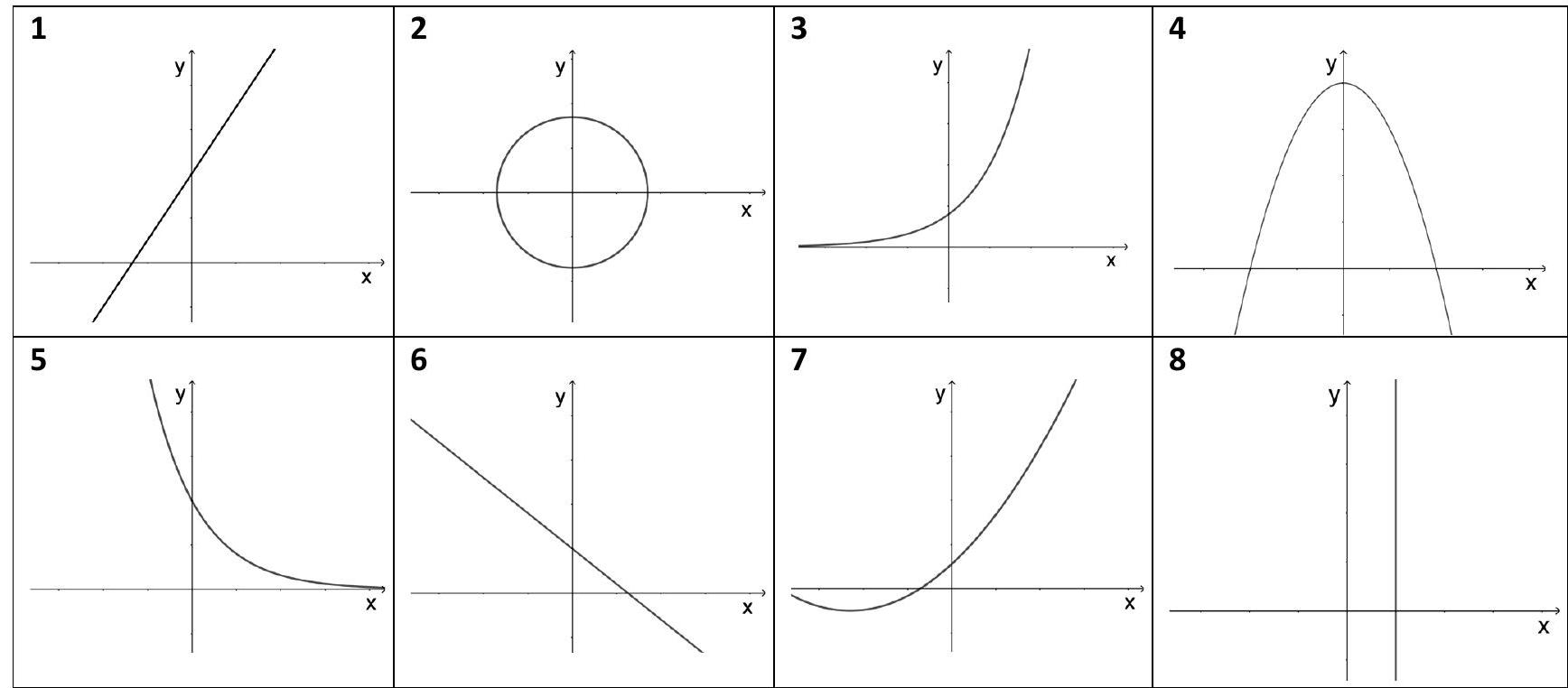
Trage die Nummern der Graphen richtig in die Tabelle ein. (3 BE)
Du kannst die Nummern mit der Maus ziehen und in der Tabelle ablegen.
Löse die Gleichung schriftlich. (2 BE)
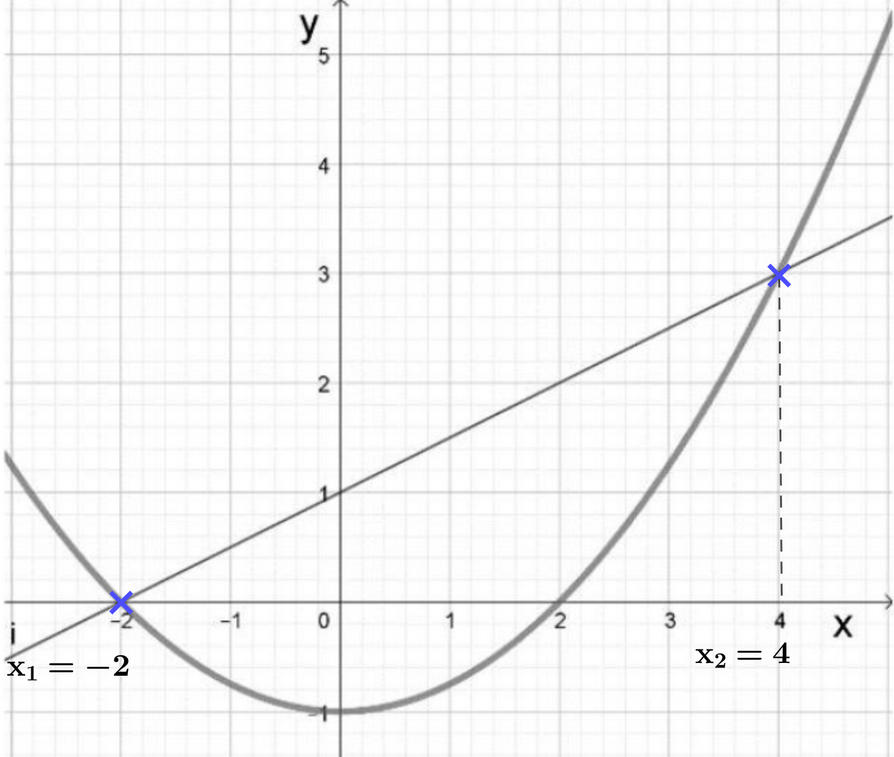
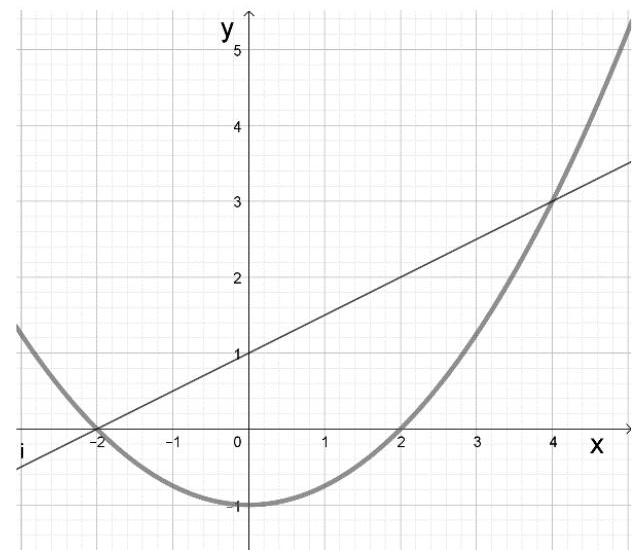
Janina möchte die Gleichung grafisch lösen.
Sie hat die Zeichnung rechts angefertigt.
Erkläre, warum mithilfe der Zeichnung die Gleichung gelöst werden kann und gib die Lösungen an. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?