Hilfsmittelfreier Teil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben zu Prüfung IGS G 2022, Hilfsmittelfreier Teil. Zum Download hier.

1
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 1
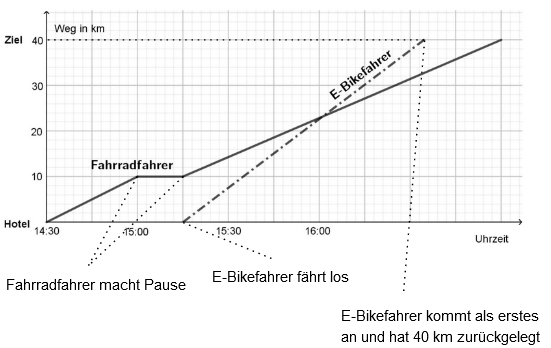
In einem Hotel kann man Fahrräder und E-Bikes ausleihen. Im Koordinatensystem ist der Verlauf der Fahrt eines Fahrradfahrers und eines E-Bikefahrers dargestellt. Sie fahren den gleichen Weg vom Hotel zum Ziel.
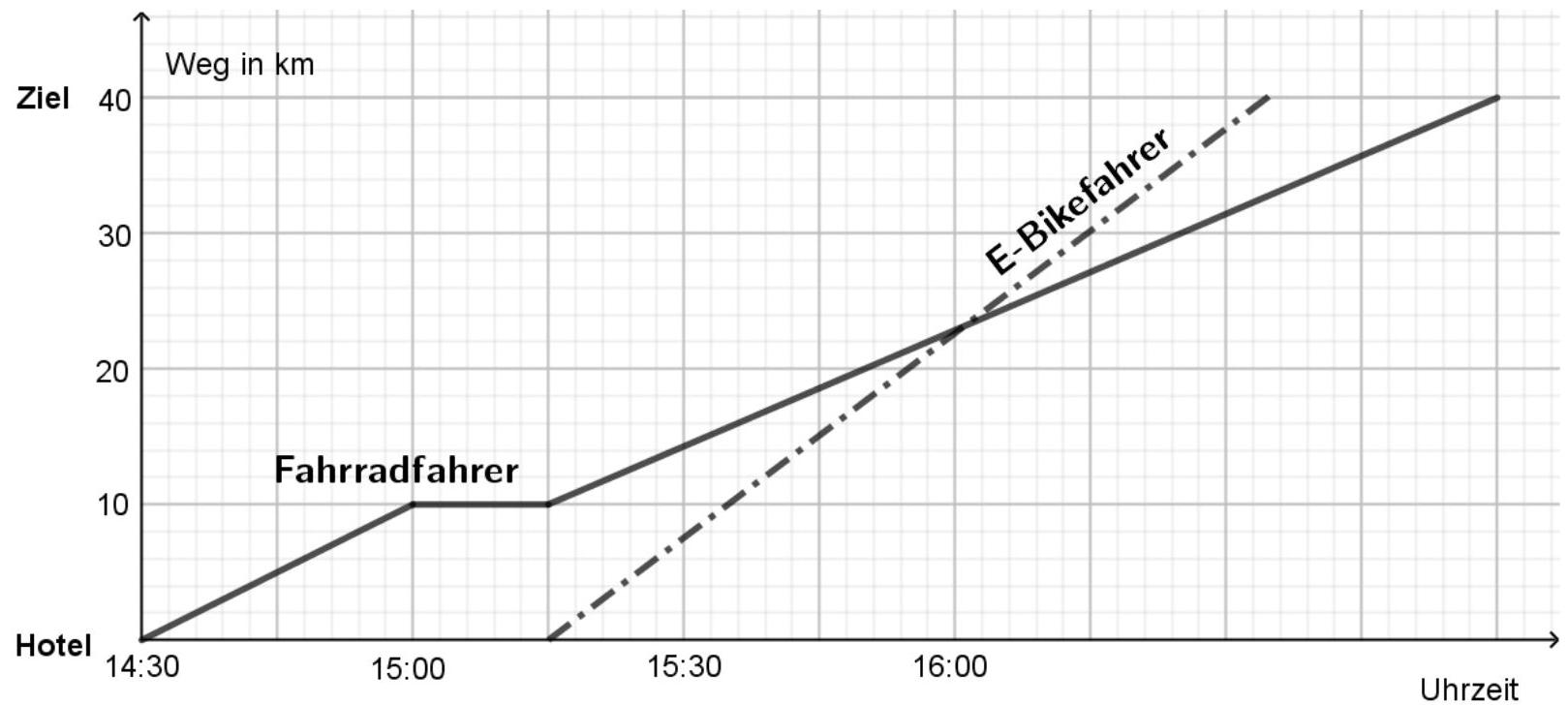
1. Fülle die Lücken aus: (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Richtiger Text
  Der Fahrradfahrer startet um 14:30 Uhr am Hotel.
  Er legt eine Pause von 15:00 Uhr bis 15:15 Uhr ein.
  Der E-Bikefahrer startet um 15:15 Uhr. Er startet somit 45 Minuten später als der Fahrradfahrer.
  Der E-Bikefahrer ist als erstes im Ziel und hat eine Gesamtstrecke von 40 $\mathrm{km}$ zurückgelegt.
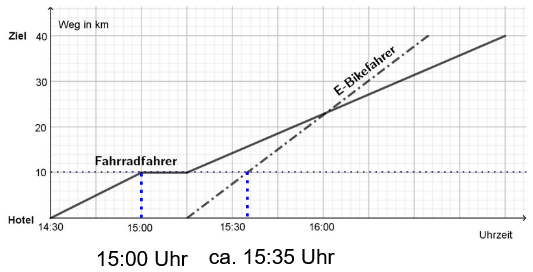
  Skizze
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies die verschiedenen Informationen aus dem Schaubild aus.
2. Nach $10 \mathrm{~km}$ befindet sich an der Strecke ein Kiosk. Markiere im Koordinatensystem, wann der Fahrradfahrer und wann der E-Bikefahrer den Kiosk erreichen. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Punkte im Koordinatensystem
  Skizze
  Gesucht sind die Punkte, die auf der Höhe des y-Werts $10~\text{km}$ liegen.
  Für den Fahrradfahrer ist dieser bei: 15:00 Uhr
  Für den E-Bikefahrer ist dieser bei: ~15:35 Uhr
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere die Punkte, wo die Graphen den y-Wert $10$ erreichen.
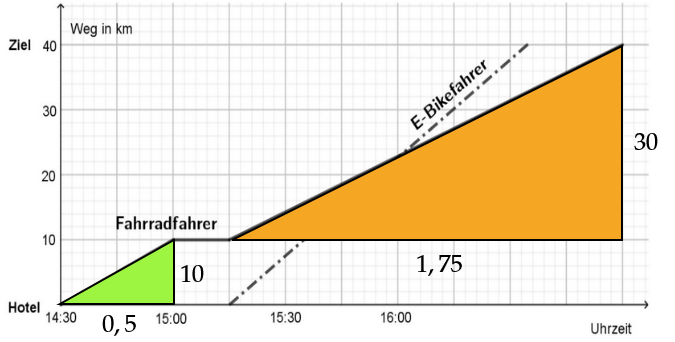
3. Entscheide, ob der Fahrradfahrer vor oder nach der Pause schneller gefahren ist. Begründe deine Entscheidung. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
  Steigungen messen
  Steigungsdreiecke
  Vor der Pause hat der Fahrradfahrer $10~\text{km}$ in $0{,}5~\text{h}$ zurückgelegt. Das entspricht einer Geschwindigkeit von:
  $\frac{}{}$ $\dfrac{10~\text{km}}{0{,}5~\text{h}}=20~\dfrac{\text{km}}{\text{h}}$
  Nach der Pause wurden $30~\text{km}$ in $1{,}75~\text{h}$ zurückgelegt, was eine Geschwindigkeit von
  $\dfrac{30~\text{km}}{1{,}75~\text{h}}\approx 17{,}14~\dfrac{\text{km}}{\text{h}}$
  ergibt.
  Vor der Pause ist der Radfahrer schneller gefahren.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Miss die Steigung der beiden Geraden in den Abschnitten vor und nach der Pause.
  Vergleiche und entscheide, wann der Fahrer schneller gefahren ist.
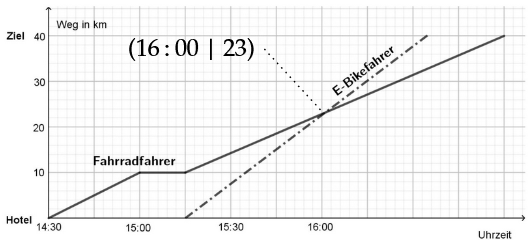
4. Gib den ungefähren Schnittpunkt der beiden Graphen an und erkläre die Bedeutung im Sachzusammenhang. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Funktionen
  Schnittpunkt bestimmen
  Schaubild
  Der ungefähre Schnittpunkt der beiden Geraden liegt etwa bei:
  Schnittpunkt im Sachzusammenhang
  Im Schnittpunkt stimmen Zeit und Ort der Fahrer überein. Sie begegnen sich in diesem Punkt. Genau genommen überholt der E-Bikefahrer in diesem Punkt den Fahrradfahrer.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies den Schnittpunkt anhand des Schaubilds ab.
  Interpretiere, was passiert ist wenn Ort und Zeit der beiden Fahrer übereinstimmen.
2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 2
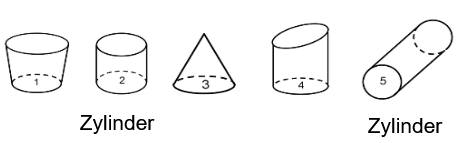
Hier siehst du verschiedene Körper:
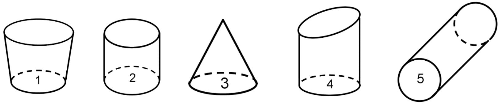
1. Trage die Nummern der Körper in die Tabelle ein. (1 BE)
  Du kannst die Nummern mit der Maus ziehen und in der Tabelle ablegen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
  Schaubild - Nr. 2 und Nr. 5 sind Zylinder
  Korrekt ausgefüllte Tabelle
  Nummern der Körper
  Zylinder
  2, 5
  kein Zylinder
  1, 3, 4
  Körper 1 ist kein Zylinder, weil die Radien der beiden Kreise verschieden sind, Körper 3 ist keiner, weil es nur einen Kreis auf der Oberfläche gibt. Bei Körper 4 sind die ebenen Flächen nicht parallel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
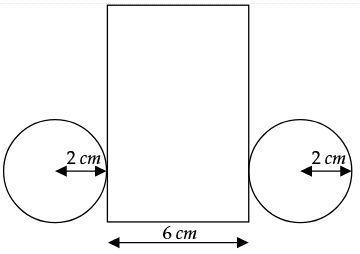
2. Gegeben ist ein Zylinder mit folgenden Maßen: $r=2~\text{cm},~h=6~\text{cm},~u=12{,}6~\text{cm}$
  Zeichne ein Netz für den Zylinder im Maßstab 1:1. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Körpernetze
  Mögliche Lösung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Das Netz besteht aus zwei Kreisen und einem Rechteck
3. Friederike hat die Formel für die Berechnung der Oberfläche des Zylinders aufgestellt.
  Erkläre, was sie falsch gemacht hat. (2 BE)
  Friederikes Formel: $O=\pi\cdot2^2+2\cdot\pi \cdot 2\cdot 6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
  Die Formel für die Oberfläche wäre allgemein:
  Es scheint so, als hätte Friederike eine Kreisfläche vergessen. In ihrer Formel fehlt der Faktor $2$ im Term für die Kreisflächen, somit berechnet sie nur eine.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Untersuche die einzelnen Terme. Grundsätzlich könnte Friederike:
  Terme vergessen haben
  Falsche Werte eingesetzt haben
  Rechenzeichen falsch gesetzt haben
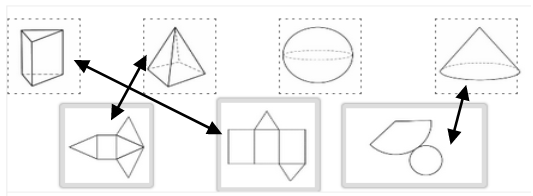
4. Im Folgenden siehst du vier Körper.
  Ordne jedem Körper das passende Netz zu, indem du die Netze mit der Maus auf den Körper ziehst.
  Benenne den übriggebliebenen Körper. (2 BE)
  
  Richtige Zuordnung
  Zuordnung
  Namen des Körpers
  Kugel
  Der übriggebliebene Körper ist eine Kugel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 3
Ralf, Yasmin und Martin werfen zwei Münzen.
Sie vereinbaren folgende Regel:
Ralf gewinnt, wenn beide Münzen Zahl zeigen.
Martin gewinnt, wenn beide Münzen Kopf zeigen.
Yasmin gewinnt in allen anderen Fällen.
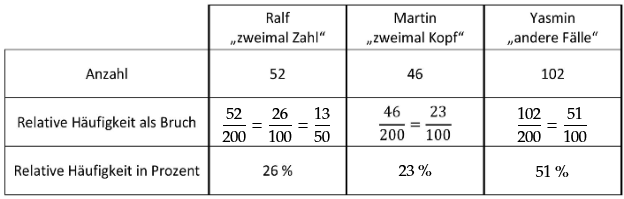
1. Die Münzen werden 200-mal geworfen und die Ergebnisse in einer Tabelle notiert.
  Vervollständige die Tabelle. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Rechne die Angaben in einen Bruch um.
  Schreibe hierzu die Anzahl der Treffer als Zähler und $200$ als Nenner.
  Bestimme die Häufigkeit in Prozent.
  Diese kann aus dem Bruch $\dfrac{...}{100}$ direkt ausgelesen werden.
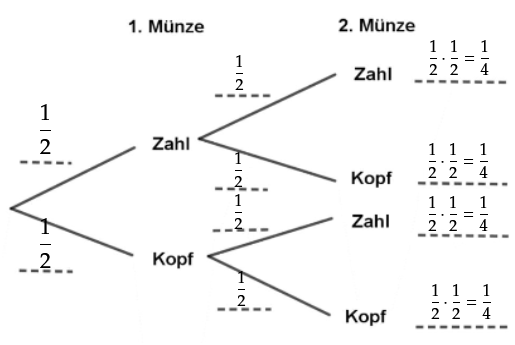
2. Martin möchte die Gewinnwahrscheinlichkeiten des Spiels untersuchen.
  Trage die Wahrscheinlichkeiten für das Werfen der Münzen in das Baumdiagramm ein. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Wahrscheinlichkeit beim Münzwurf
  Der Münzwurf ist ein Laplace-Experiment. Alle Elementareignisse, also "Kopf" und "Zahl" sind gleich wahrscheinlich.
  $P("\text{Kopf}")=P("\text{Zahl}")=\frac12$
  Baumdiagramm
  Baumdiagramm
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Wahrscheinlichkeiten beim Werfen einer Münze
  Fülle beide Stufen aus. Beachte, dass die Wahrscheinlichkeiten aller Stufen gleich bleiben.
  Berechne jeweils die Wahrscheinlichkeit entlang der Pfade und trage sie rechts ein.
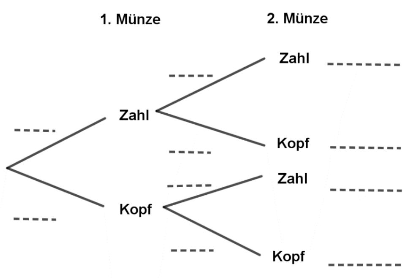
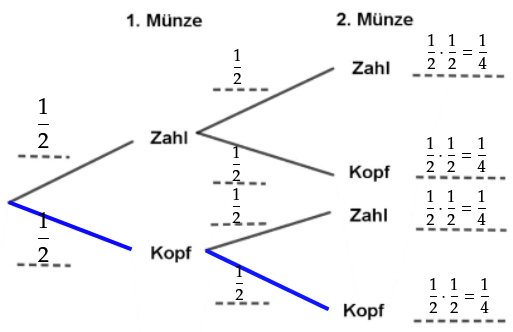
3. Färbe den Gewinnpfad für Martin im Baumdiagramm. (1 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Martins Gewinnpfad ist "Kopf-Kopf"
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
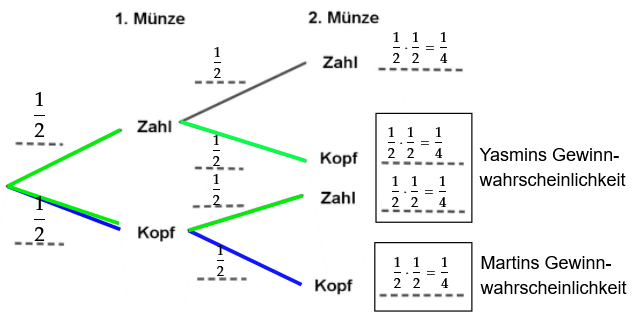
4. Martin meint:
  „Das Spiel ist unfair. Yasmins Wahrscheinlichkeit zu gewinnen ist doppelt so hoch wie meine.“
  Erkläre, warum Martin recht hat. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Yasmins Gewinnpfade
  Gewinnpfade beider Personen
  Wahrscheinlichkeit
  Aus dem Diagramm lässt sich bestimmen:
  Yasmin gewinnt mit einer Wahrscheinlichkeit+ von $\frac14+\frac14=\frac12$
  Martin gewinnt mit einer Wahrscheinlichkeit von $\frac14$
  Yasmins Wahrscheinlichkeit ist doppelt so hoch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme Yasmins Gewinnpfade, ähnlich wie in Teilaufgabe (c) Martins Pfad.
  Vergleiche die Wahrscheinlichkeiten.