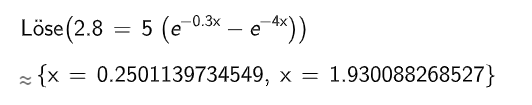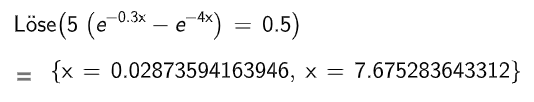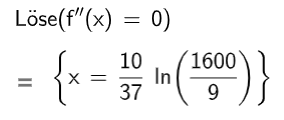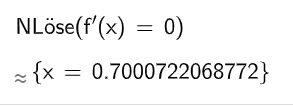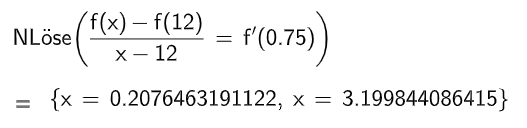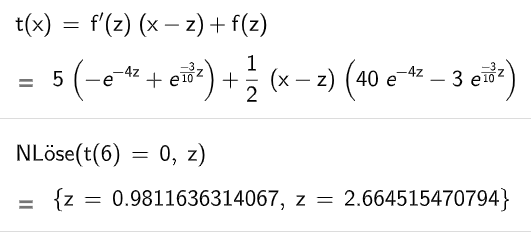Aufgabe 1A
Die auf definierte Funktion mit modelliert für die Konzentration eines Medikamentenwirkstoffes im Blut. Dabei beschreibt die Zeit in Stunden nach der Einnahme des Medikamentes und die Konzentration im Blut in Milligramm pro Liter .
Berechnen Sie die Konzentration eine Stunde nach der Einnahme des Medikamentes. Geben Sie den Zeitpunkt an, zu dem die Konzentration erstmals den Wert 2,8 annimmt.
Bestimmen Sie, wie lange die Konzentration mindestens beträgt. (6BE)
Bestimmen Sie und interpretieren Sie den Wert im Sachzusammenhang. (2BE)
Berechnen Sie den Zeitpunkt, zu dem die Konzentration am stärksten abnimmt. (3BE)
Die Konzentration im Blut sollte möglichst eine Stunde vor dem Schlafengehen am größten sein.
Berechnen Sie, wie viele Stunden vor dem Schlafengehen das Medikament optimalerweise eingenommen werden sollte. (4BE)
Für hat die Gleichung keine Lösung.
Interpretieren Sie diese Aussage im Sachkontext. (2BE)
Untersuchen Sie, ob es ein Zeitintervall gibt, in dem die durchschnittliche Änderungsrate der Konzentration so groß ist wie die momentane Änderungsrate der Konzentration Stunden nach der Einnahme. (4BE)
Vier Stunden nach der ersten Einnahme wird das Medikament in der gleichen
Dosierung erneut eingenommen. Die Gesamtkonzentration ist zu jedem Zeitpunkt die Summe der Konzentrationen, die sich aus der ersten und zweiten Einnahme ergeben. Ermitteln Sie die Gesamtkonzentration eine Stunde nach der zweiten Einnahme.
Die Gesamtkonzentration soll nicht übersteigen.
Untersuchen Sie, ob diese Vorgabe eingehalten wird. (6BE)
Eine vereinfachte Modellierung geht davon aus, dass die Konzentration ab einem bestimmten Zeitpunkt durch die Tangente an den Graphen von im Punkt beschrieben werden kann.
Bestimmen Sie für den Zeitpunkt nach der Einnahme des Medikamentes, zu dem die Konzentration nach diesem vereinfachten Modell null ist. (4BE)
Untersuchen Sie, ob es nach dieser vereinfachten Modellierung einen Zeitpunkt gibt, sodass die Konzentration genau 6 Stunden nach der Einnahme null ist. (4BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?