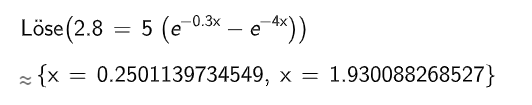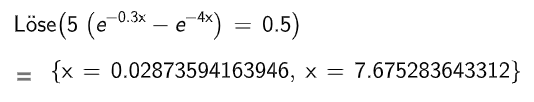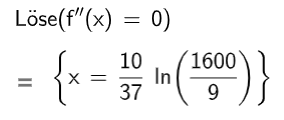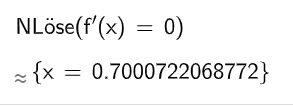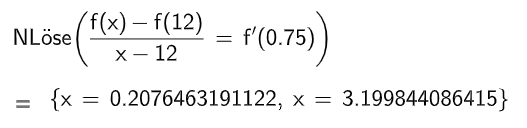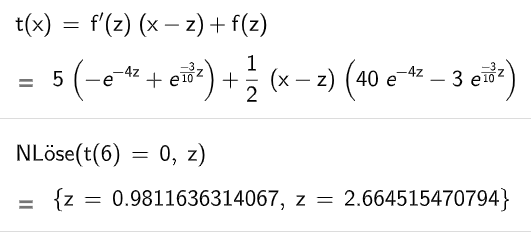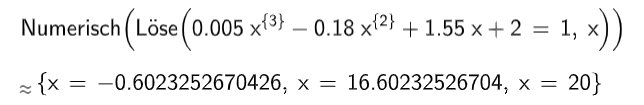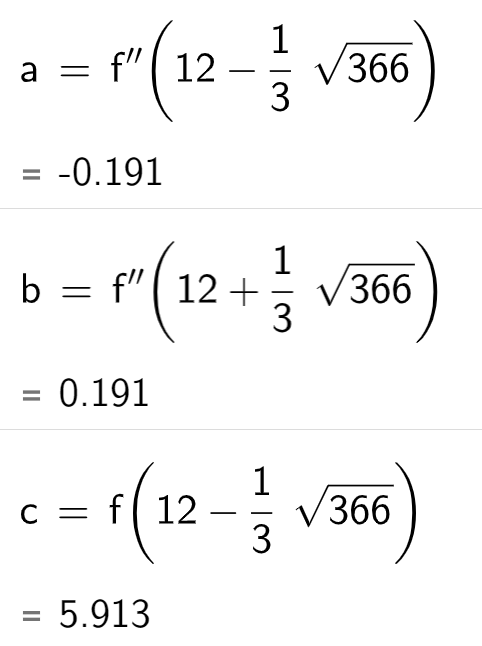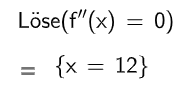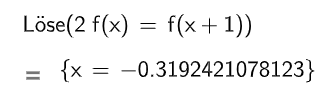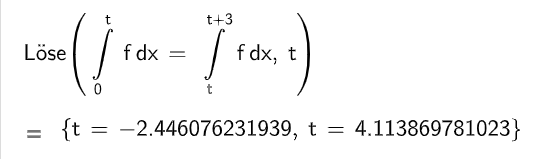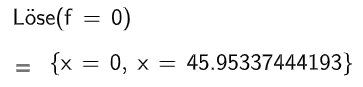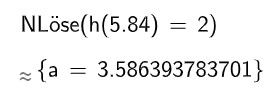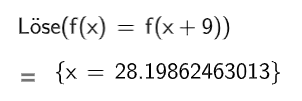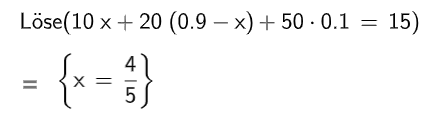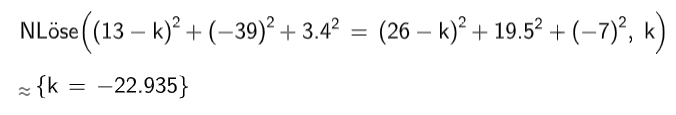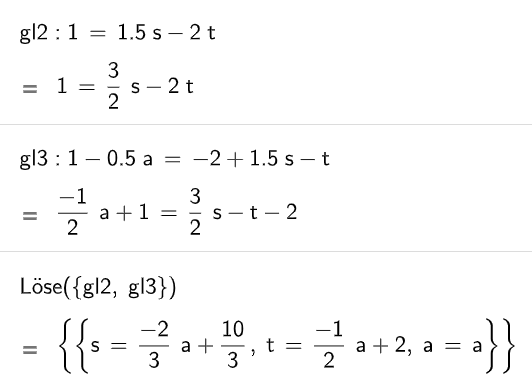Wahlteil - CAS
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe 1A
Die auf definierte Funktion mit modelliert für die Konzentration eines Medikamentenwirkstoffes im Blut. Dabei beschreibt die Zeit in Stunden nach der Einnahme des Medikamentes und die Konzentration im Blut in Milligramm pro Liter .
Berechnen Sie die Konzentration eine Stunde nach der Einnahme des Medikamentes. Geben Sie den Zeitpunkt an, zu dem die Konzentration erstmals den Wert 2,8 annimmt.
Bestimmen Sie, wie lange die Konzentration mindestens beträgt. (6BE)
Bestimmen Sie und interpretieren Sie den Wert im Sachzusammenhang. (2BE)
Berechnen Sie den Zeitpunkt, zu dem die Konzentration am stärksten abnimmt. (3BE)
Die Konzentration im Blut sollte möglichst eine Stunde vor dem Schlafengehen am größten sein.
Berechnen Sie, wie viele Stunden vor dem Schlafengehen das Medikament optimalerweise eingenommen werden sollte. (4BE)
Für hat die Gleichung keine Lösung.
Interpretieren Sie diese Aussage im Sachkontext. (2BE)
Untersuchen Sie, ob es ein Zeitintervall gibt, in dem die durchschnittliche Änderungsrate der Konzentration so groß ist wie die momentane Änderungsrate der Konzentration Stunden nach der Einnahme. (4BE)
Vier Stunden nach der ersten Einnahme wird das Medikament in der gleichen
Dosierung erneut eingenommen. Die Gesamtkonzentration ist zu jedem Zeitpunkt die Summe der Konzentrationen, die sich aus der ersten und zweiten Einnahme ergeben. Ermitteln Sie die Gesamtkonzentration eine Stunde nach der zweiten Einnahme.
Die Gesamtkonzentration soll nicht übersteigen.
Untersuchen Sie, ob diese Vorgabe eingehalten wird. (6BE)
Eine vereinfachte Modellierung geht davon aus, dass die Konzentration ab einem bestimmten Zeitpunkt durch die Tangente an den Graphen von im Punkt beschrieben werden kann.
Bestimmen Sie für den Zeitpunkt nach der Einnahme des Medikamentes, zu dem die Konzentration nach diesem vereinfachten Modell null ist. (4BE)
Untersuchen Sie, ob es nach dieser vereinfachten Modellierung einen Zeitpunkt gibt, sodass die Konzentration genau 6 Stunden nach der Einnahme null ist. (4BE)
- 2
Aufgabe 1B
Für einen Tag wird die in einen Stausee zufließende Wassermenge betrachtet.
Die momentane Zuflussrate wird durch die auf definierte Funktion mit
für beschrieben.
Dabei gibt die Zeit nach Beobachtungsbeginn in Stunden und die Zuflussrate des Wassers in 1000 Kubikmeter pro Stunde an.
Der Stausee verfügt auch über einen künstlichen Wasserablauf. Gehen Sie zunächst davon aus, dass der Ablauf am Tag der Beobachtung geschlossen ist.
Die Abbildung stellt den Graphen der Funktion dar.
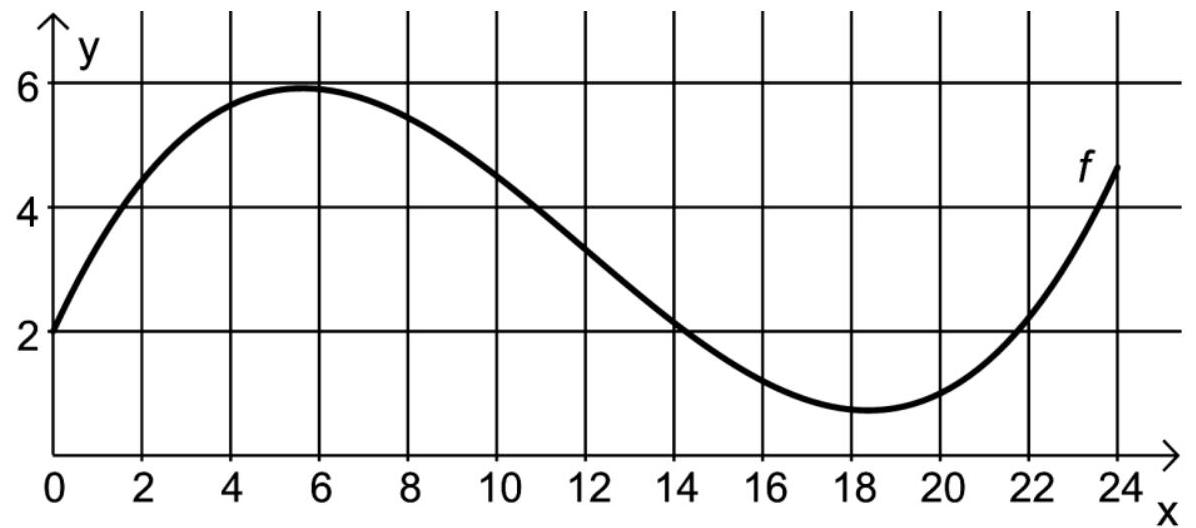
Geben Sie an und interpretieren Sie den Wert im Sachzusammenhang.
Begründen Sie mithilfe des Graphen von , dass der Wasserstand im Stausee ständig ansteigt. (4BE)
Berechnen Sie die Länge des Zeitraums, in dem die Zuflussrate geringer als ist. (3BE)
Berechnen Sie die maximale Zuflussrate im Beobachtungszeitraum. (3BE)
Bestimmen Sie die Zeitpunkte, an denen die Zuflussrate
am stärksten abnimmt.
am stärksten zunimmt.
(5BE)
Untersuchen Sie, ob es eine Zuflussrate gibt, die sich eine Stunde später verdoppelt hat. (3BE)
Vereinfacht wird die Form des Stausees als Quader mit einer Länge von und einer Breite von angenommen.
Berechnen Sie den Anstieg der Wasserhöhe innerhalb der Stunden. (4BE)
Von Beobachtungsbeginn bis zum Zeitpunkt ist eine bestimmte Wassermenge zugeflossen. In den folgenden drei Stunden fließt noch einmal genauso viel Wasser dazu.
Berechnen Sie den Zeitpunkt . (4BE)
Bei dem künstlichen Wasserablauf können konstante Abflussraten eingestellt werden.
Stunden nach Beobachtungsbeginn wird der Ablauf geöffnet.
Bestimmen Sie die Abflussrate des Stausees so, dass sich Stunden nach
Beobachtungsbeginn genauso viel Wasser im Stausee befindet wie zu Beobachtungsbeginn. (4BE)
m³/hDer Wasserablauf wird zu Beobachtungsbeginn mit einer Abflussrate von geöffnet.
Begründen Sie auch mithilfe einer Skizze und ohne Rechnung, dass etwa zum
Zeitpunkt die Wassermenge im Stausee maximal ist. (5BE)
- 3
Aufgabe 1C
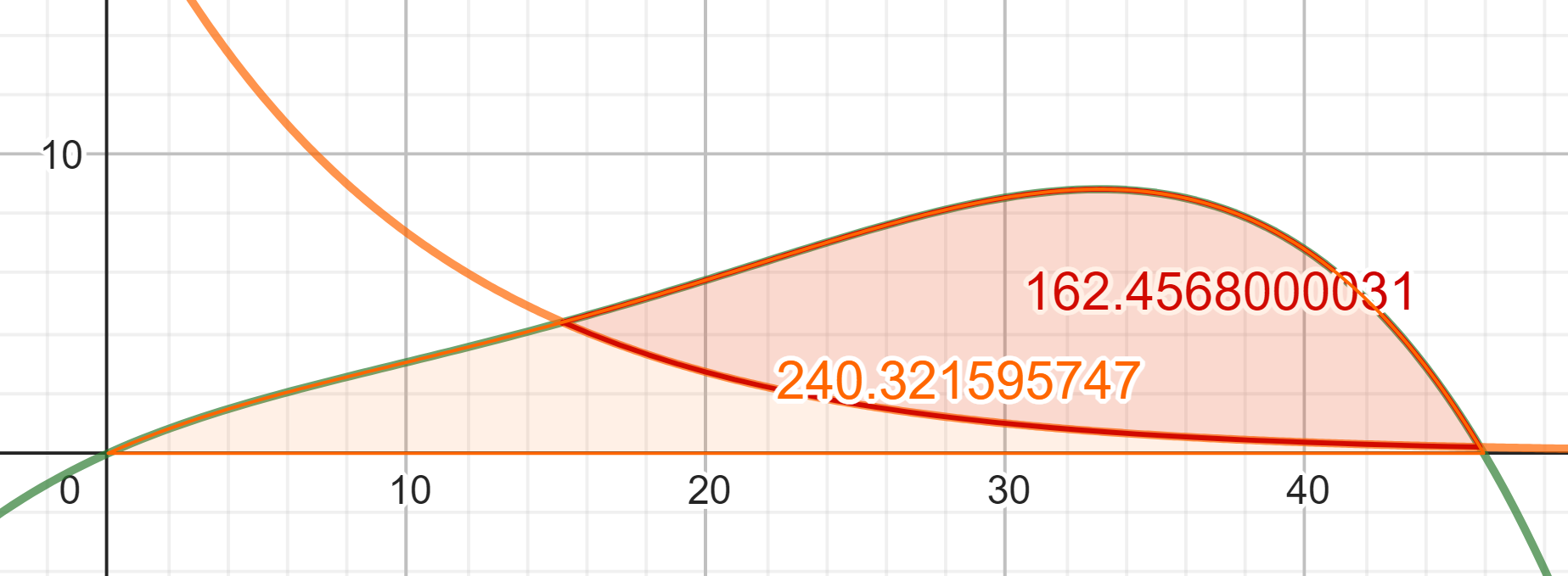
Gegeben ist die auf definierte Funktion mit . Der Querschnitt eines Deichs wird durch die von dem Graphen der Funktion und der -Achse eingeschlossenen Fläche modelliert. Dabei werden und in Metern angegeben.
Die Abbildung zeigt den Graphen von . Markieren Sie in der Abbildung auf der -Achse das Intervall, in dem der Deich mindestens hoch ist.
Ein moderner Deich ist etwa fünfmal so breit wie er hoch ist.
Entscheiden Sie, ob dieser Deich diese Regel erfüllt, und begründen Sie Ihre Entscheidung nur mithilfe der Abbildung. (5BE)
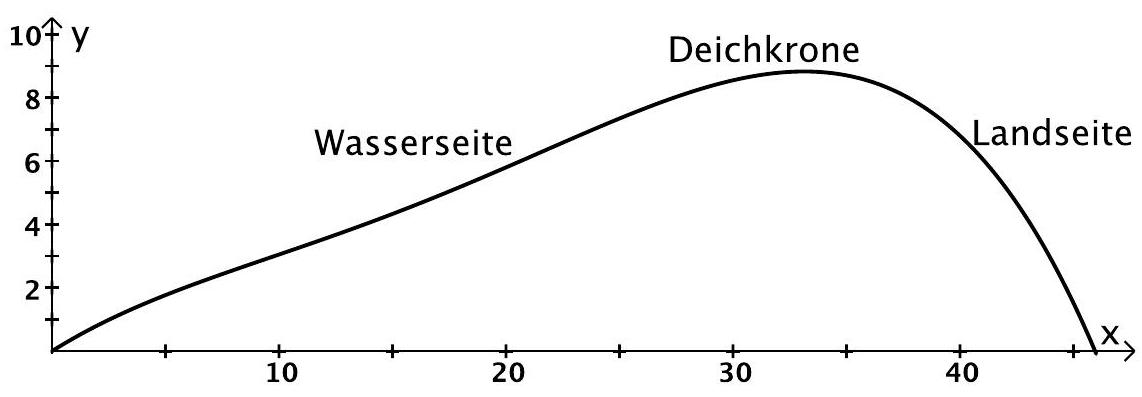
Berechnen Sie die durchschnittliche Steigung des Deichs im Intervall .
Bestimmen Sie die größte Steigung des Deichs im Intervall
Berechnen Sie den Neigungswinkel des Deichs an der Stelle . (9BE)
In den Deich eindringendes Wasser teilt den Querschnitt des Deiches in einen unteren feuchten und einen oberen trockenen Bereich. Die Trennlinie zwischen dem trockenen und feuchten Bereich nennt man Sickerlinie. Bei einem bestimmten Wasserstand wird die Sickerlinie innerhalb des Deichs durch die auf definierte Funktion mit beschrieben. und werden in Metern angegeben.
Berechnen Sie die Höhe, in der die Sickerlinie auf der Wasserseite des Deichs beginnt.
Begründen Sie ohne Rechnung, dass die Sickerlinie stets oberhalb des Bodens verläuft.
Berechnen Sie den prozentualen Anteil des feuchten Bereichs im Querschnitt des
Deichs. (10BE)
Die Sickerlinie verändert sich mit dem Wasserstand. Sie wird beschrieben durch die auf definierte Funktion mit und in Metern .
Bestimmen Sie einen Näherungswert für , sodass den Beginn der Sickerlinie in der Höhe von auf der Wasserseite beschreibt. (4BE)
Der Bereich der Deichkrone soll abgeplattet werden. Dazu wird Material abgetragen. Der Querschnitt des Deichs wird dabei so verändert, dass der obere Rand im Bereich der Deichkrone parallel zur Horizontalen verläuft.
Berechnen Sie die Breite des abgeplatteten Bereichs, wenn der Deich genau hoch sein soll.
Berechnen Sie die Höhe des Deichs, wenn der abgeplattete Bereich breit ist. (7BE)
- 4
Aufgabe 2A
In einem Bundesland wird die Bevölkerungsgruppe derjenigen, die im Jahr geboren wurden, im Hinblick auf Schulabschlüsse untersucht. In dieser Bevölkerungsgruppe beträgt der Anteil der Personen mit Abitur . Unter den Personen mit Abitur sind weiblich. der Bevölkerungsgruppe sind nicht weiblich und haben kein Abitur.
Weisen Sie nach, dass unter allen Personen ohne Abitur der Anteil derjenigen, die nicht weiblich sind, etwa beträgt. (2BE)
Stellen Sie den Sachzusammenhang in einem beschrifteten Baumdiagramm dar. (3BE)
Zur betrachteten Bevölkerungsgruppe gehören Personen.
Ermitteln Sie, wie viele dieser Personen weiblich sind. (3BE)
Für eine Online-Befragung werden aus der betrachteten Bevölkerungsgruppe Personen zufällig ausgewählt. Es soll davon ausgegangen werden, dass unter den ausgewählten Personen die Anzahl derjenigen mit Abitur binomialverteilt ist.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter den ausgewählten Personen mit Abitur sind. (1BE)
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Anzahl der ausgewählten Personen mit Abitur kleiner als der Erwartungswert dieser Anzahl ist. (3BE)
Die Wahrscheinlichkeit dafür, dass die Anzahl der ausgewählten Personen mit Abitur im Intervall liegt, beträgt etwa .
Bestimmen Sie die Werte für und so, dass das Intervall symmetrisch um den Erwartungswert liegt. (4BE)
Aus der anfangs betrachteten Bevölkerungsgruppe werden Personen zufällig ausgewählt. Die Wahrscheinlichkeit dafür, dass sich darunter mehr als mit Abitur befinden, ist größer als und kleiner als .
Ermitteln Sie alle Werte, die für infrage kommen. (4BE)
- 5
Aufgabe 2B
Bei einem Smartphone-Spiel kann jeder Spieler jeden Sonntag Sterne gewinnen. Dazu hat er an jedem Sonntag zehn Versuche. Bei jedem Versuch kann nur ein Stern gewonnen werden; die Wahrscheinlichkeit dafür beträgt .
Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein Spieler bei zehn Versuchen mehr als sechs Sterne gewinnt. (2BE)
Beurteilen Sie die Gültigkeit der folgenden Aussage eines Spielers: (2BE)
"Ich habe an den letzten drei Sonntagen jeweils acht Sterne gewonnen. Daher ist die Wahrscheinlichkeit, an diesem Sonntag wieder acht Sterne zu gewinnen, deutlich kleiner als vorher.“
An einem Sonntag nutzen vier Spieler jeweils die möglichen zehn Versuche zum Gewinnen von Sternen.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass dabei zwei der vier Spieler jeweils fünf Sterne gewinnen. (3BE)
Die Wahrscheinlichkeit dafür, bei einem Versuch einen Stern zu gewinnen, wird geändert. Anschließend beträgt die Wahrscheinlichkeit dafür, bei zehn Versuchen höchstens drei Sterne zu gewinnen, etwa
Ermitteln Sie die geänderte Wahrscheinlichkeit dafür, bei einem Versuch einen Stern zu gewinnen, auf ganze Prozent genau. (3BE)
Außerdem hat jeder Spieler täglich einmal die Möglichkeit, allein durch Starten des Spiels Bonuspunkte zu erhalten. Durch das Starten wird ihm automatisch eine zufällig bestimmte Anzahl von Bonuspunkten gutgeschrieben. Der Tabelle können die möglichen Anzahlen und die zugehörigen Wahrscheinlichkeiten entnommen werden.

Ein Spieler startet das Spiel an drei aufeinanderfolgenden Tagen.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass dieser Spieler von Tag zu Tag weniger Bonuspunkte erhält. (2BE)
Ein Spieler startet das Spiel an vier Tagen. Bestimmen Sie die Wahrscheinlichkeit dafür, dass dieser Spieler dabei insgesamt Bonuspunkte erhält. (4BE)
Die Wahrscheinlichkeiten für und Bonuspunkte werden so geändert, dass die Spieler im Zeitraum von Tagen, an denen das Spiel gestartet wird, im Mittel Bonuspunkte erhalten.
Ermitteln Sie die beiden geänderten Wahrscheinlichkeiten. (4BE)
- 6
Aufgabe 2C
Ein Unternehmen produziert Leiterplatten zum Einbau in elektronische Geräte. Aus Erfahrung weiß man, dass der Leiterplatten fehlerhaft sind. Leiterplatten werden zufällig ausgewählt. Die Anzahl der fehlerhaften Leiterplatten unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter den ausgewählten Leiterplatten
Leiterplatten fehlerhaft sind.
maximal Leiterplatten fehlerhaft sind.
mehr als aber weniger als Leiterplatten fehlerhaft sind.
(5BE)
Geben Sie die Bedeutung des folgenden Terms im Sachzusammenhang an:
(2BE)
Jede fehlerhafte Leiterplatte wird untersucht. Sie weist entweder Fehler oder Fehler auf. Die Wahrscheinlichkeit für Fehler beträgt , die für Fehler beträgt .
Beim Standardverfahren wird der vorliegende Fehler mit absoluter Sicherheit gefunden. Es wird zunächst Fehler gesucht. Falls dieser an keiner Stelle vorliegt, muss die Stelle gesucht werden, an der Fehler vorliegt. Die Suche von Fehler kostet , die Suche von Fehler kostet .
Geben Sie die Kosten an, die dem Unternehmen entstehen, wenn bei einer Leiterplatte der Fehler gefunden wird.
Weisen Sie nach, dass die zu erwartenden Kosten für das Standardverfahren
pro Leiterplatte betragen. (4BE)
Um Kosten einzusparen, wird für die fehlerhaften Leiterplatten ein Schnelltest vorgeschlagen: In diesem wird bei den fehlerhaften Leiterplatten ausschließlich Fehler gesucht. Dieser Schnelltest kostet nur , allerdings wird ein vorhandener Fehler nur in der Fälle gefunden.
Wird mit diesem Schnelltest der Fehler nicht gefunden, wird anschließend das Standardverfahren durchgeführt.
Begründen Sie, dass die Wahrscheinlichkeit dafür, dass Fehler in diesem Schnelltest nicht gefunden wird, beträgt.
Bestimmen Sie unter der Bedingung, dass bei dem Schnelltest Fehler nicht gefunden wurde, die Wahrscheinlichkeit dafür, dass der vorhandene Fehler trotzdem Fehler ist. (4BE)
Untersuchen Sie, ob sich die zu erwartenden Kosten pro Leiterplatte für die Fehlersuche mit Schnelltest und Standardverfahren tatsächlich verringern. (5BE)
- 7
Aufgabe 3A
Die Abbildung zeigt die Pyramide mit
und .
Die Grundfläche ist quadratisch.
Der Schnittpunkt der Diagonalen der Grundfläche wird mit bezeichnet.
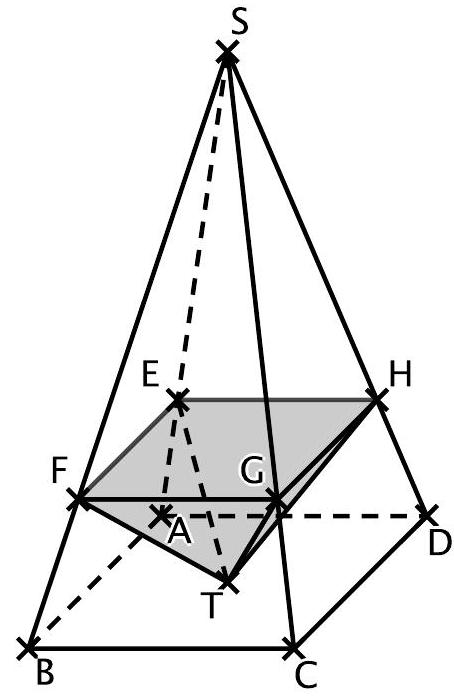
Geben Sie die Koordinaten des Punktes an.
Berechnen Sie den Inhalt der Oberfläche der Pyramide . (6BE)
Bestimmen Sie die Größe des Winkels zwischen den Kanten und . (3BE)
Der Mittelpunkt der Kante wird mit bezeichnet.
Untersuchen Sie, ob es einen Punkt auf der Kante gibt, für den das Dreieck im Punkt rechtwinklig ist. (5BE)
Die vier Punkte und liegen jeweils auf einer der vier vom Punkt ausgehenden Kanten und haben alle die -Koordinate (vgl. Abbildung).
Gegeben ist die folgende Lösung einer Aufgabe im Zusammenhang mit den betrachteten geometrischen Objekten:
liefert und damit und .
Geben Sie eine passende Aufgabenstellung an und erläutern Sie den Ansatz der gegebenen Lösung. (3BE)
Ermitteln Sie das Volumen der Pyramide . (3BE)
- 8
Aufgabe 3B
Das Rechteck stellt ein Tennisspielfeld dar. Die Koordinaten für die folgenden Punkte lauten: und .
Alle Koordinaten haben die Längeneinheit Fuß (ft). Das Netz ist an Pfosten befestigt, die durch die Strecken und dargestellt sind. Es hat an den Enden eine Höhe von 3,5 ft und fällt geradlinig ab, bis es in der Mitte nur noch eine Höhe von hat. Der Boden wird durch die -Ebene dargestellt. Der Ball wird als punktförmig angenommen.
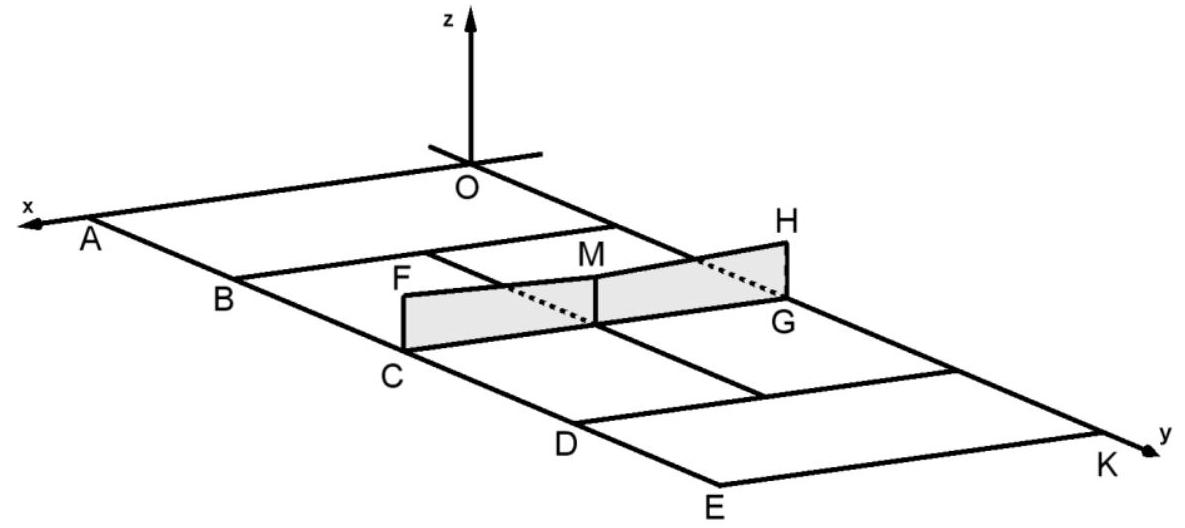
Geben Sie die Koordinaten der Punkte und an.
Berechnen Sie die Länge der Diagonalen des Spielfeldes. (4BE)
Bei einem Aufschlag wird der Ball im Punkt getroffen und fliegt in Richtung . Er trifft im Punkt auf dem Boden auf. Es kann vorausgesetzt werden, dass der Ball das Netz überquert und dass die -Koordinate zu diesem Zeitpunkt größer als ist. Die Flugbahn des Balls wird als geradlinig angenommen.
Bestimmen Sie die Koordinaten des Punktes, in dem der Ball sich über dem Netz befindet. [Zur Kontrolle: ]
Berechnen Sie die Höhe des Netzes an der Stelle, an der der Ball das Netz überquert.
(7BE)
Spiegelt man die Gerade, die die Flugbahn des Balles beschreibt, an der -Ebene, ergibt sich die Gerade . Die Gerade beschreibt die Flugbahn direkt nach dem Aufprall.
Bestimmen Sie eine Gleichung der Gerade . (4BE)
Im Punkt , befindet sich eine Kamera. Sie zeichnet die Flugbahn des Balles von Punkt nach Punkt auf.
Bestimmen Sie den Wert von so, dass die Kamera den gleichen Abstand zu Punkt
und zu Punkt hat. (5BE)
- 9
Aufgabe 3C
In einem Koordinatensystem mit Ursprung sind die folgenden Vektoren gegeben:
und
Zeigen Sie die Gültigkeit folgender Aussagen:
Es gibt Werte für und , sodass gilt:
und sind nicht kollinear.
(4BE)
Die Gerade durch die Punkte und wird mit bezeichnet.
Die Gerade durch die Punkte und wird mit bezeichnet.
Begründen Sie nur mit den Aussagen aus Teilaufgabe a), dass sich und in genau einem Punkt schneiden. (3BE)
Die Geraden und liegen in der Ebene mit der Gleichung
.
Für jeden Wert von wird ein Punkt betrachtet.
Geben Sie eine Gleichung der Geraden durch und an. (2BE)
Zeigen Sie, dass der Punkt für jeden Wert von in der Ebene liegt. (4BE)
Berechnen Sie den Wert von , sodass sich die Gerade und die Gerade durch die Punkte und orthogonal schneiden. (3BE)
Bestimmen Sie den Wert von , für den der Abstand von und minimal ist. (4BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?