Prüfungsaufgaben Mathematik 2023

Funktionen (10 Punkte)

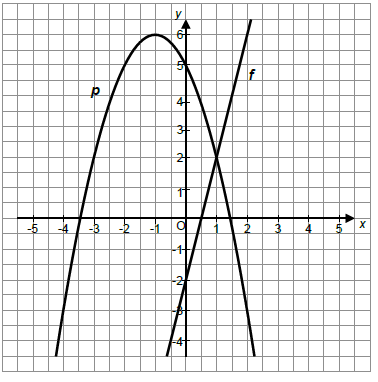
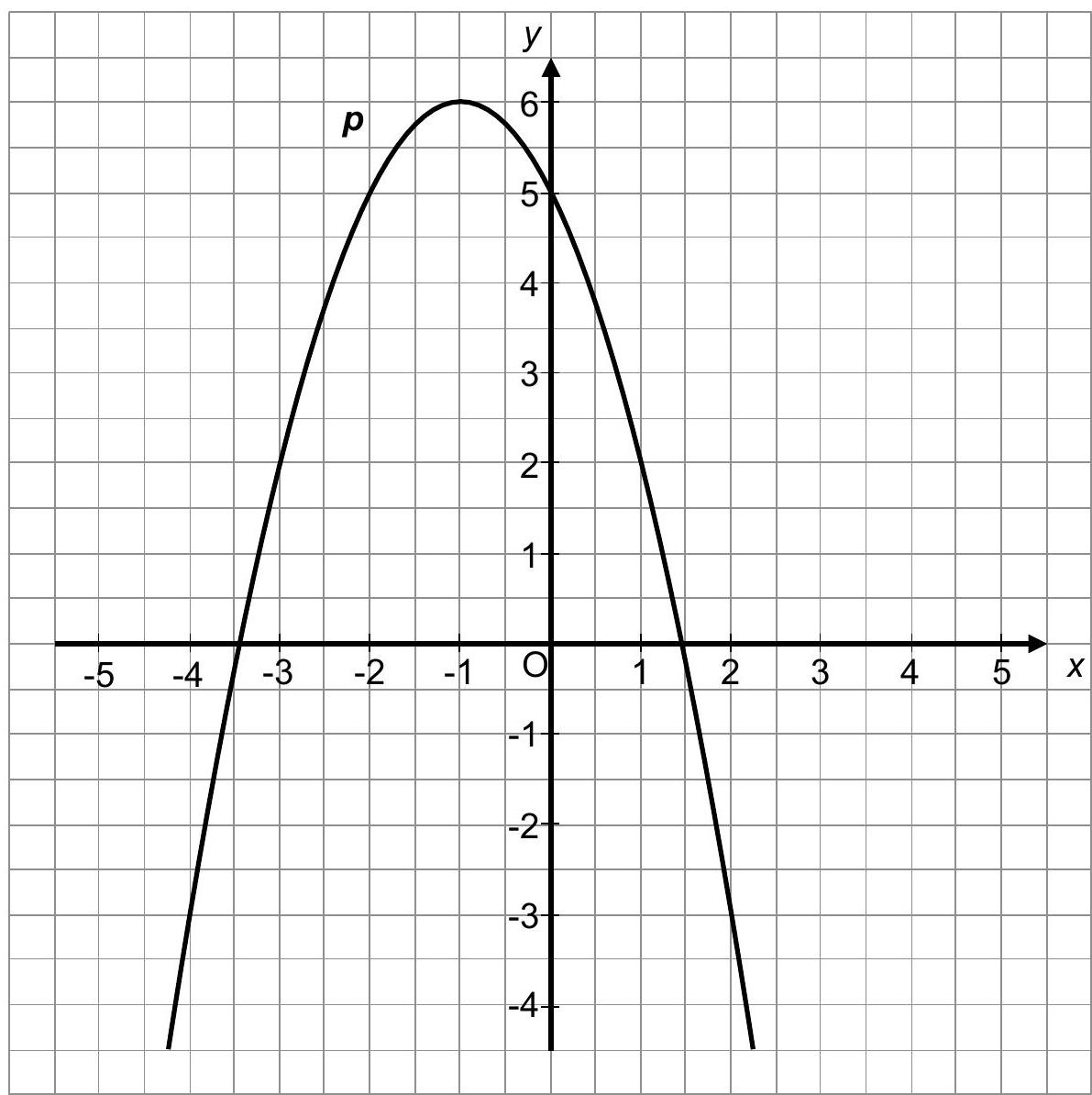
Im Koordinatensystem ist die Normalparabel $p$ dargestellt.

Die Gerade $f$ hat die Gleichung $f (x) = 4 x - 2$ .
Zeichnen Sie die Gerade $f$ in das vorgegebene Koordinatensystem.
Geben Sie die Koordinaten eines Schnittpunktes der beiden Graphen an. (2P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Funktionen
Darstellung der Graphen
Ein Schnittpunkt ist $S (1 | 2)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind. Ordnen Sie zu. (3P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Steigung der Funktion $f$
$f (x) = m \cdot x + b$
$f (x) = 4 x - 2$
Steigung: $m = 4$
Die Aussage "Die Steigung der linearen Funktion $f$ ist negativ" ist falsch.
Schnittpunkte von Parabel und Gerade
Parabel: $p (x) = - x^{2} - 2 x + 5$
Gerade: $f (x) = 4 x - 2$
$- x^{2} - 2 x + 5$ $=$ $4 x - 2$
↓
fasse zusammen
$- x^{2} - 6 x + 7$ $=$ $0$ $: (- 1)$
$x^{2} + 6 x - 7$ $=$ $0$
Mitternachtsformel:
$x_{1,2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
$x_{1,2} = \frac{- 6 \pm \sqrt{36 + 28}}{2}$
$x_{1,2} = \frac{- 6 \pm 8}{2}$
$x_{1} = 1$
$x_{2} = - 7$
Die Aussage "Die Gerade und die Parabel schneiden sich in zwei Punkten" ist richtig.
Schnittpunkt der Funktion f mit der y-Achse
Die Gerade $f$ schneidet die $y$ -Achse im Punkt $(0 | - 2)$
Die Aussage "Die Gerade $f$ schneidet die $y$ -Achse im Punkt $(- 2 ∣ 0)$ ist falsch.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Entscheide, ob die Gerade steigt oder fällt.
Die letzteren Aussagen können durch Berechnung des Schnittpunkts untersucht werden.
$*$ Geben Sie die Koordinaten des Scheitelpunktes der Parabel $p$ an. $S (\dots | \dots)$
Notieren Sie eine Gleichung der Parabel $p$ in der Scheitelpunktform.
(2P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
Scheitelpunkt aus dem Graphen ablesen
Der Scheitelpunkt ist $S (- 1 | 6)$ .
Verwendung der Scheitelform zur Bestimmung der Gleichung der Parabel
$p (x) = - (x + 1)^{2} + 6$
Achte dabei auf das Minuszeichen vor der Klammer, da die Parabel nach unten geöffnet ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Lies den Scheitelpunkt aus dem Graphen ab.
Setze die Koordinaten des Scheitelpunkts in die Scheitelform ein.
$*$ Die Parabel $p$ hat die Gleichung $p (x) = - x^{2} - 2 x + 5$ .
Bestimmen Sie die $x$ -Koordinaten derjenigen Punkte der Parabel $p$ , deren $y$ -Koordinate -10 ist. (3P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
$- 10$ $=$ $- x^{2} - 2 x + 5$ $+ 10$
$0$ $=$ $- x^{2} - 2 x + 15$ $\cdot (- 1)$
↓
Verwendung der pq-Formel
$=$ $x^{2} + 2 x - 15$
$x_{1,2}$ $=$ $- \frac{2}{2} \pm \sqrt{(\frac{2}{2})^{2} + 15}$
$x_{1,2}$ $=$ $- 1 \pm \sqrt{16}$
$=$ $- 1 \pm 4$
$x_{1}$ $=$ $3$
$x_{2}$ $=$ $- 5$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze $p (x) = y = - 10$ in die Gleichung ein und löse nach $x$ auf

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$- x^{2} - 2 x + 5$	$=$	$4 x - 2$
	↓	fasse zusammen
$- x^{2} - 6 x + 7$	$=$	$0$	$: (- 1)$
$x^{2} + 6 x - 7$	$=$	$0$

$- 10$	$=$	$- x^{2} - 2 x + 5$	$+ 10$
$0$	$=$	$- x^{2} - 2 x + 15$	$\cdot (- 1)$
	↓	Verwendung der pq-Formel
	$=$	$x^{2} + 2 x - 15$
$x_{1,2}$	$=$	$- \frac{2}{2} \pm \sqrt{(\frac{2}{2})^{2} + 15}$
$x_{1,2}$	$=$	$- 1 \pm \sqrt{16}$
	$=$	$- 1 \pm 4$
$x_{1}$	$=$	$3$
$x_{2}$	$=$	$- 5$

Funktionen (10 Punkte)

Darstellung der Graphen

Hast du eine Frage oder Feedback?

Steigung der Funktion f

Schnittpunkte von Parabel und Gerade

Schnittpunkt der Funktion f mit der y-Achse

Hast du eine Frage oder Feedback?

Scheitelpunkt aus dem Graphen ablesen

Verwendung der Scheitelform zur Bestimmung der Gleichung der Parabel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Steigung der Funktion $f$