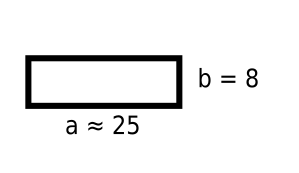Prüfungsaufgaben Mathematik 2023
🎓 Prüfungsbereich für Berlin
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Formelsammlung, die bei der Prüfung beiliegt.
- 1
Basisaufgaben (10 Punkte)
Nora benötigt für mit dem Fahrrad Minuten.
Geben Sie an, wie viele Minuten sie bei gleicher Geschwindigkeit für braucht. (1P)
minTim gewinnt bei einem Wettbewerb einen Geldpreis.
Er schenkt des Gewinnes seinen Eltern. Das sind .
Geben Sie die gesamte Gewinnsumme an. (1P)
€Ein Rechteck hat einen Flächeninhalt von .
Es ist breit.
Geben Sie die Länge des Rechtecks an. (1P)
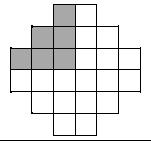
mmMarkieren Sie in der nebenstehenden Figur der Fläche. (1P)
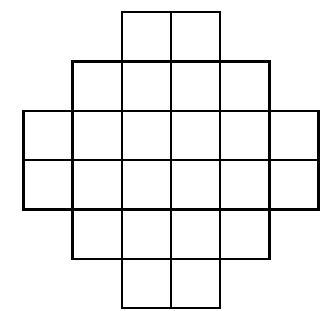
Geben Sie die Lösung der Gleichung an. (1P)
Geben Sie den kleinsten Wert an. (1P)
Gegeben ist das Dreieck . (2P)
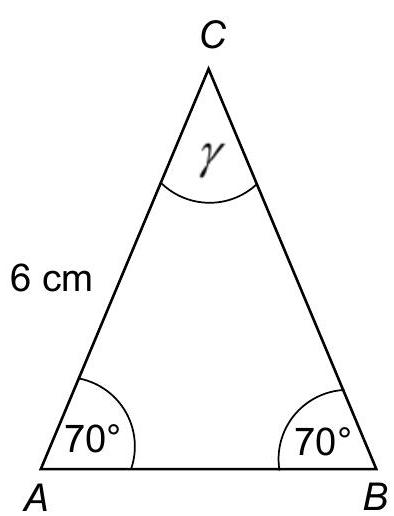
(Skizze nicht maßstabsgerecht)
Die Differenz aus dem Doppelten einer Zahl und wird verdreifacht.
Kreuzen Sie den zugehörigen Term an. (1P)
Einer der folgenden Punkte liegt nicht auf der Geraden mit der Gleichung .
Entscheiden Sie, welcher Punkt das ist. Kreuzen Sie an. (1P)
- 2
Trapez (6 Punkte)
Gegeben ist das folgende Trapez.
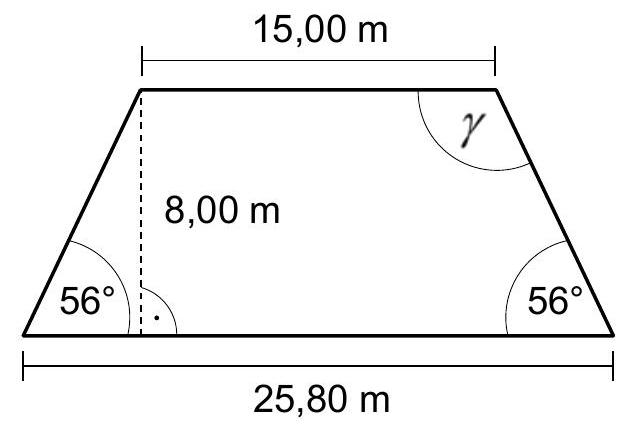
(Skizze nicht maßstabsgerecht)
Geben Sie die Größe des Winkels an. (1P)
Berechnen Sie den Flächeninhalt des Trapezes. (2P)
Berechnen Sie den Umfang des Trapezes. (3P)
- 3
Umzug (7 Punkte)
Herr Mert benötigt ein Mietfahrzeug für seinen Umzug.
Er holt sich zwei Angebote ein.
Angebot 1
Angebot 2
- Miete pro Tag - insgesamt kostenfrei - jeder zusätzliche Kilometer
- einmalig Miete für eine Woche - jeder Kilometer
Die Kosten für die Anmietung für einen Tag sollen für die Angebote 1 und 2 in einem Diagramm dargestellt werden.
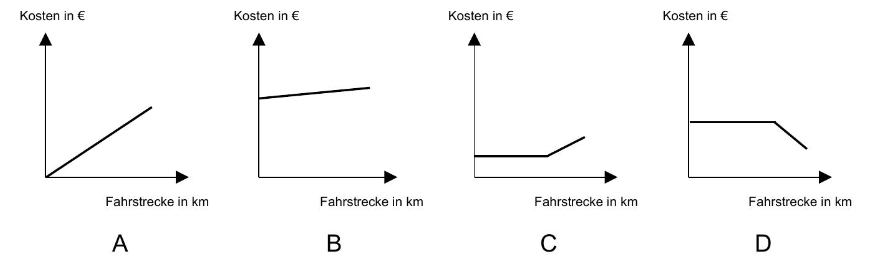
Geben Sie für jedes Angebot das passende Diagramm an. (2P)
Herr Mert benötigt das Mietfahrzeug von Montag bis Freitag.
Er muss insgesamt fahren.
Berechnen Sie die Gesamtkosten für beide Angebote.
Entscheiden Sie, welches Angebot günstiger ist.
Stellen Sie für das Angebot 2 eine Gleichung zur Berechnung der Gesamtkosten für beliebige bei einer Woche Mietdauer auf.
(5P)
- 4
Funktionen (10 Punkte)
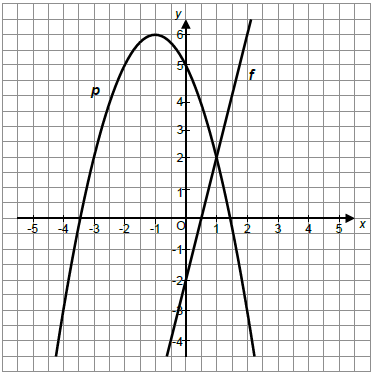
Im Koordinatensystem ist die Normalparabel dargestellt.
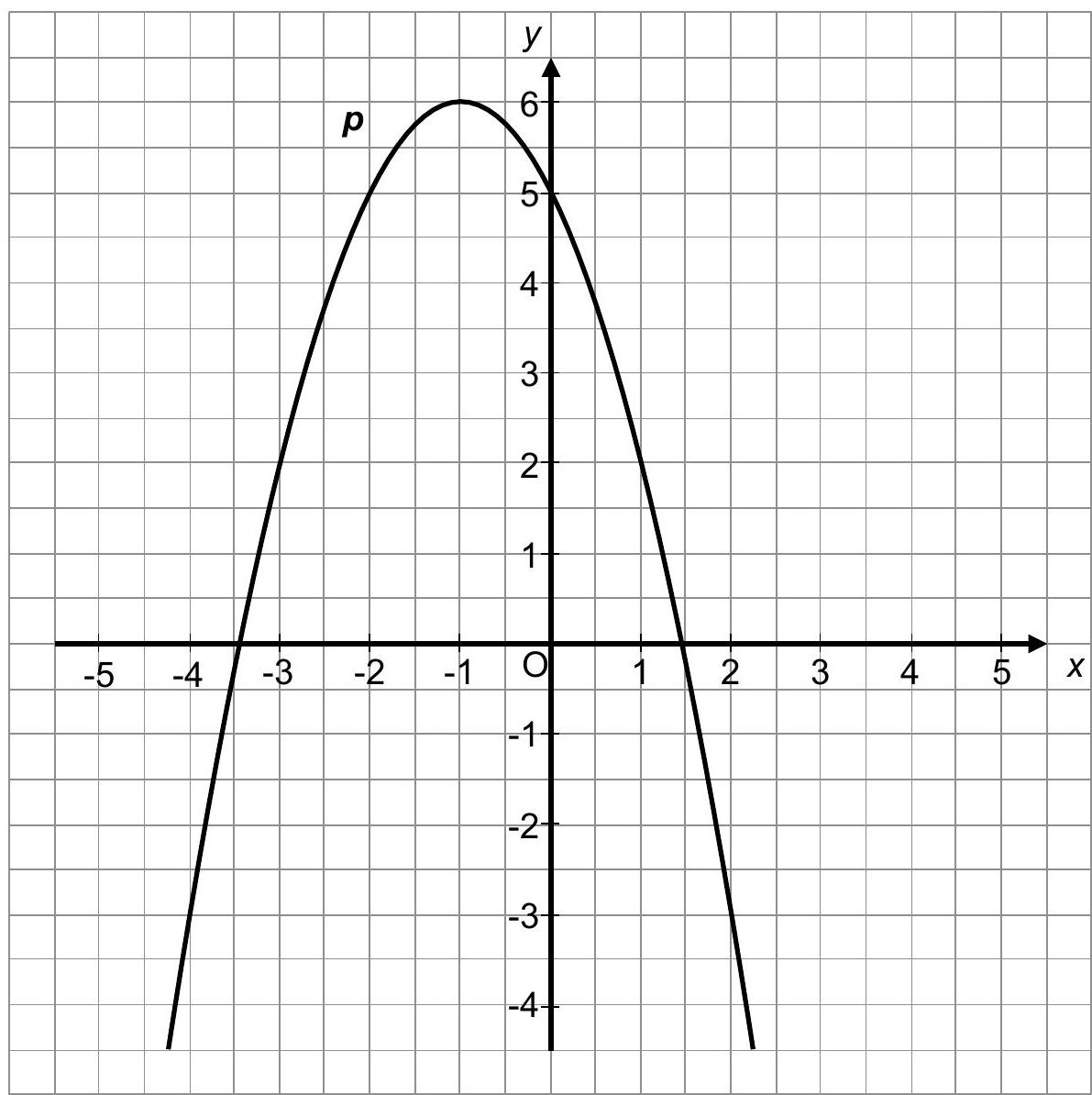
Die Gerade hat die Gleichung .
Zeichnen Sie die Gerade in das vorgegebene Koordinatensystem.
Geben Sie die Koordinaten eines Schnittpunktes der beiden Graphen an. (2P)
Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind. Ordnen Sie zu. (3P)
Geben Sie die Koordinaten des Scheitelpunktes der Parabel an.
Notieren Sie eine Gleichung der Parabel in der Scheitelpunktform.
(2P)
Die Parabel hat die Gleichung .
Bestimmen Sie die -Koordinaten derjenigen Punkte der Parabel , deren -Koordinate -10 ist. (3P)
- 5
Konservendose (12 Punkte)
Eine zylinderförmige Konservendose hat folgende Maße:
Radius:
Höhe:
(Skizze nicht maßstabsgerecht)
Skizzieren Sie die Mantelfläche der Konservendose.
Bestimmen Sie die Länge und Breite der Mantelfläche und beschriften Sie Ihre Skizze entsprechend. (3P)
Laut Hersteller hat die Konservendose ein Volumen von ca. .
Weisen Sie nach, dass diese Angabe richtig ist.
Hinweis: entspricht . (2P)
Die Deckel der Konservendosen werden aus rechteckigen Blechstreifen hergestellt. Diese Blechstreifen sind breit und lang. Aus einem Blechstreifen sollen so viele Deckel wie möglich hergestellt werden.
Der Materialverlust (Abfall) eines Blechstreifens bei der Produktion der Deckel soll nicht mehr als betragen.
Überprüfen Sie rechnerisch, ob die Vorgabe des Materialverlustes erfüllt ist. (4P)
Die hergestellten Deckel sollen auch für größere Konservendosen mit einem Volumen von 1 Liter verwendet werden.
Ermitteln Sie die Höhe der großen Konservendose. (3P)
- 6
Weltbevölkerung (10 Punkte)
Im Jahr 2020 lebten auf der Erde etwa Milliarden Menschen.
Kinder (0 bis 14 Jahre)
1,95 Milliarden
Jugendliche (15 - 24 Jahre)
Milliarden
mittleres Alter (25 - 64 Jahre)
Milliarden
höheres Alter (ab 65 Jahre)
Milliarden
Berechnen Sie, wie viel Prozent aller Menschen weltweit im Jahr 2020 Jugendliche waren. (2P)
Eine der folgenden zwei Aussagen passt nicht zu den Angaben aus der Tabelle.
Kreuzen Sie die falsche Aussage an und formulieren Sie dazu eine korrigierte Aussage, die zu den Angaben aus der Tabelle passt. (2P)
Es gibt vermutlich mehr als Sprachen auf der Welt.
In der Tabelle sind die fünf meist gesprochenen Sprachen angegeben.
Sprache
Anzahl der Menschen
mit dieser Muttersprache (in Millionen)
Arabisch
Chinesisch
Englisch
Hindi
Spanisch
Geben Sie Minimum, Maximum und die Spannweite der Datenreihe an. (3P)
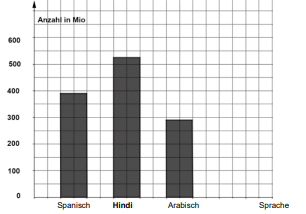
Einige Daten aus der Tabelle sind im Diagramm dargestellt.
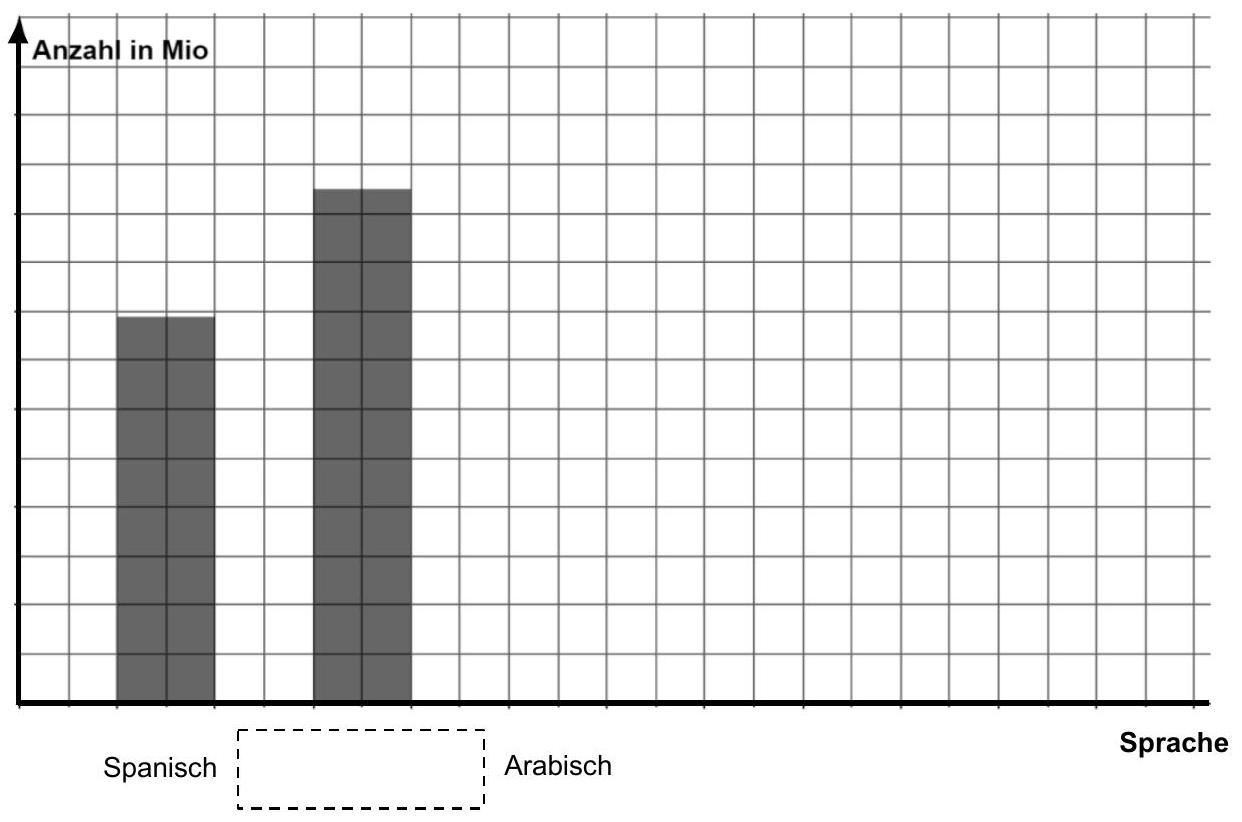
Ergänzen Sie die fehlende Einteilung der -Achse.
Notieren Sie unter der zweiten Säule die entsprechende Sprache.
Zeichnen Sie im Diagramm die Säule für „Arabisch“ ein. (3P)
- 7
Dreiecke (5 Punkte)
Gegeben ist das Dreieck .
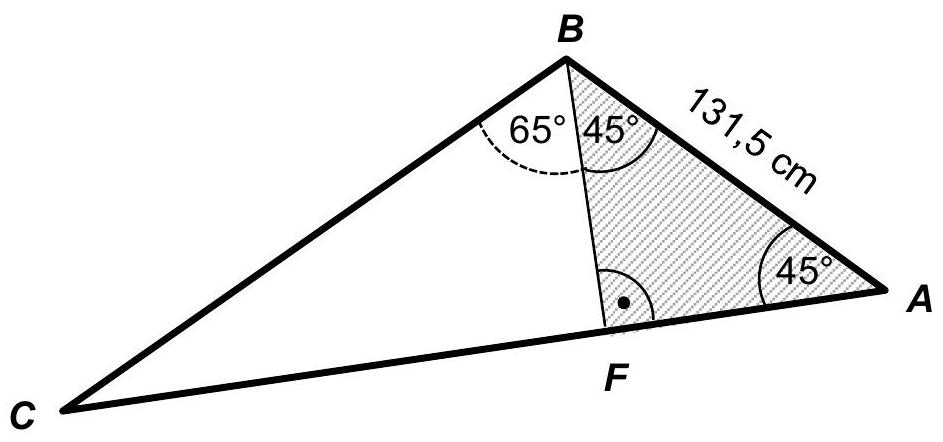
(Skizze nicht maßstabgerecht)
Begründen Sie, dass das Dreieck gleichschenklig ist. (1P)
Weisen Sie nach, dass die Länge der Strecken und jeweils ca. beträgt.
Berechnen Sie die Länge der Strecke .
(4P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?