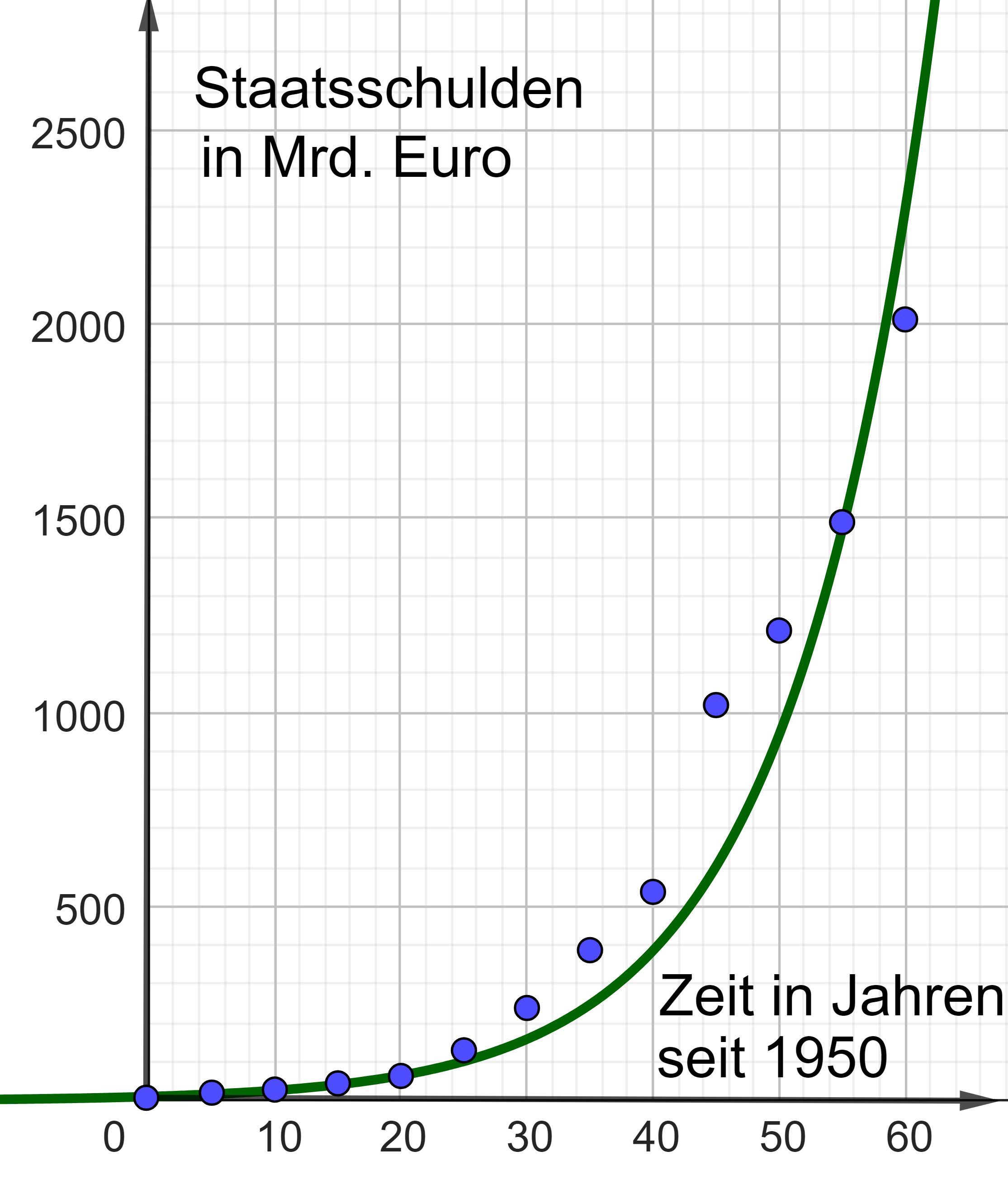
Aufgabe 1B
Die Grafik zeigt die Schulden Deutschlands zu Beginn eines Jahres für die Jahre bis in Mrd. Euro.
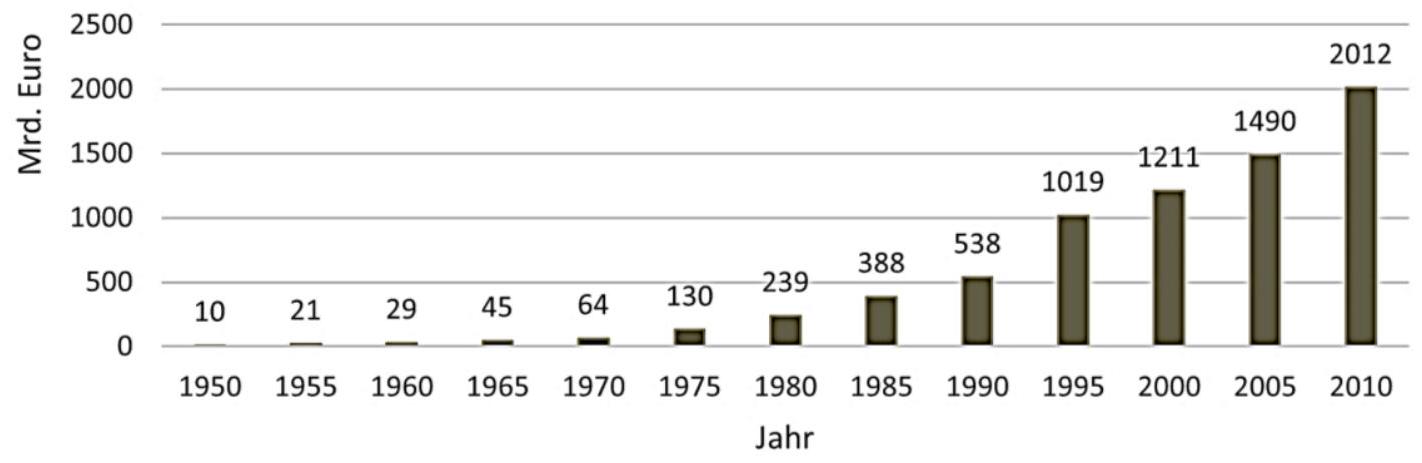
Geben Sie die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben. (2BE)
Geben Sie ein Verfahren an zur Bestimmung einer Funktion, die für den Zeitraum von bis die Schulden in Abhängigkeit von der Zeitdauer seit näherungsweise beschreibt.
Nennen Sie drei Schritte der Durchführung des Verfahrens. (4BE)
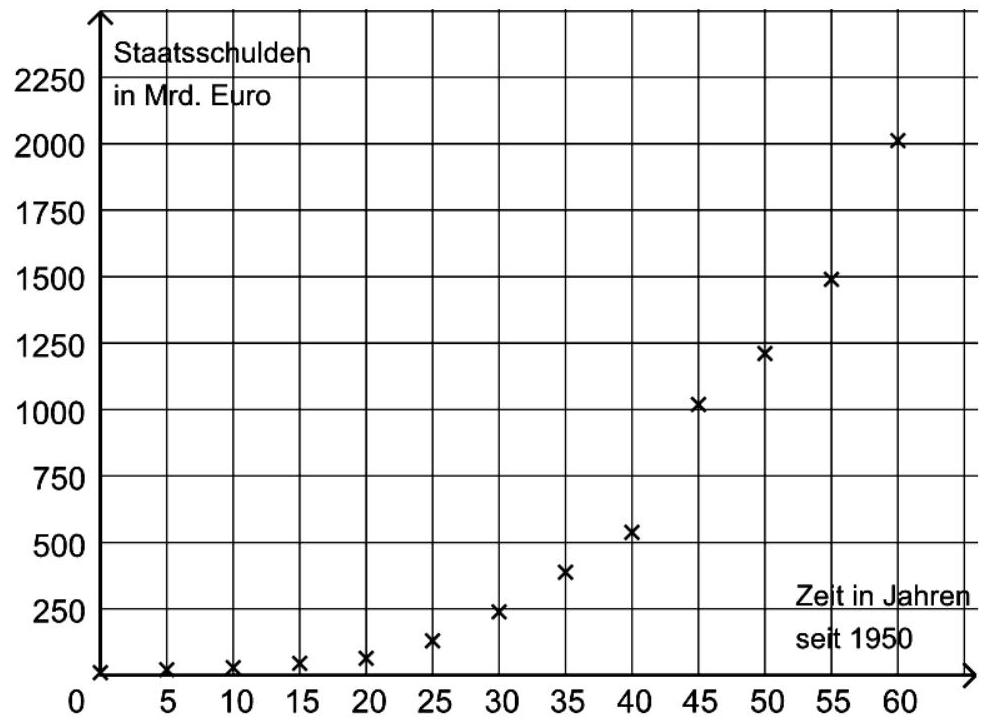
In der nebenstehenden Abbildung sind die Daten aus der Grafik eingetragen.
Die auf ganz definierte Funktion mit beschreibt für näherungsweise die Schulden Deutschlands von bis . Dabei gibt die Zeit in Jahren seit an und die Schulden in Mrd. Euro.
Zeichnen Sie den Graphen von in die Abbildung. (3BE)
Bestimmen Sie mithilfe der Funktion die jährliche prozentuale Zunahme der Schulden.
Untersuchen Sie, ob es einen Zeitpunkt gibt, zu dem die momentane Änderungsrate der Schulden größer als Mrd. Euro pro Jahr ist. (5BE)
Im Folgenden wird in einem anderen Modell die momentane Änderungsrate der Schulden Deutschlands zu Beginn eines Jahres ab dem Jahr 2005 betrachtet. Sie wird für durch die auf ganz definierte Funktion mit beschrieben.
Dabei gibt die Zeit in Jahren seit 2005 und die momentane Änderungsrate der Schulden in Mrd. Euro pro Jahr an.
Ohne Nachweis können Sie verwenden, dass mit eine Stammfunktion von ist.
Begründen Sie, dass in der Modellierung mit die momentane Änderungsrate der Schulden ab Beginn des Jahres abnimmt.
Berechnen Sie das Jahr, in dem die Schulden ihren Höchststand erreichen. (6BE)
Im Folgenden werden die zu erwartenden Schulden Deutschlands Jahre nach dem Jahr 2005 für betrachtet.
Begründen Sie, dass sich die zu erwartenden Schulden zu Beginn des Jahres mithilfe des folgenden Terms berechnen lassen:
Bestimmen Sie das Jahr, in dem die Schulden vollständig abgebaut sind. (7BE)
Begründen Sie, dass die Lösungen der Gleichung Zeitpunkte nach dem Jahr angeben, zu denen die Schulden um der vorhandenen Schulden wachsen.
Bestimmen Sie den Zeitraum, in dem die momentane Änderungsrate der Schulden weniger als der Schulden beträgt. (8BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?