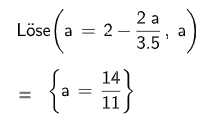Aufgabe 3A
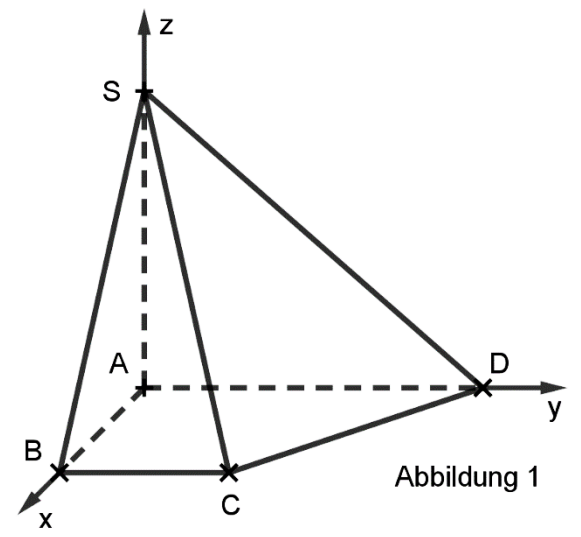
Begründen Sie, dass die Grundfläche der Pyramide ein Trapez ist.
Berechnen Sie das Volumen der Pyramide. [5 BE]
Zeigen Sie, dass das Dreieck im Punkt rechtwinklig ist. [2 BE]
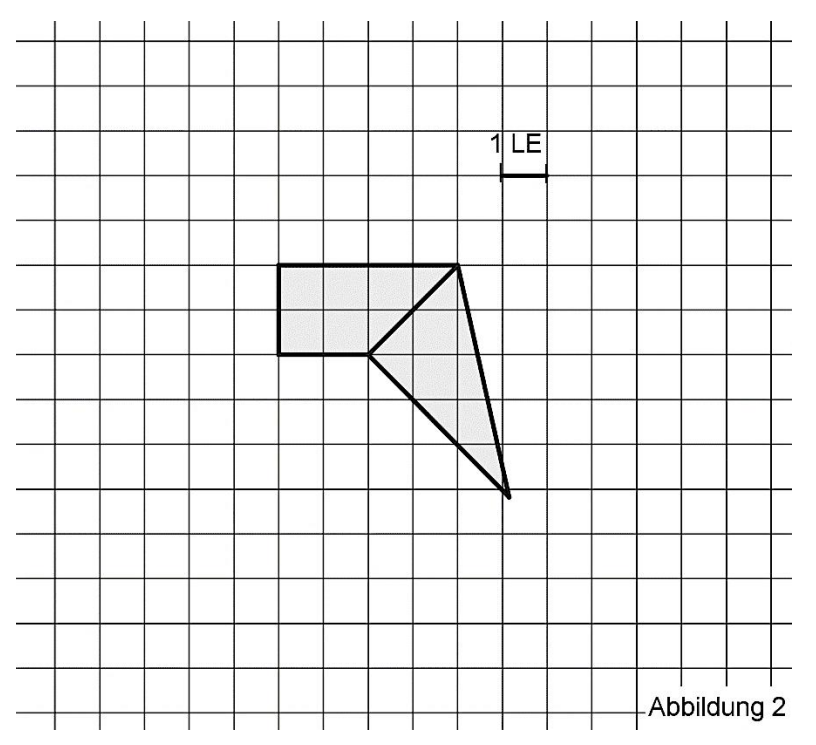
In Abbildung 2 ist ein Teil eines Netzes der Pyramide dargestellt.
Ergänzen Sie Abbildung 2 so, dass ein
vollständiges Netz der Pyramide
dargestellt ist. [4 BE]
Untersuchen Sie, ob der Punkt in der Ebene liegt, in der die Seitenfläche liegt. [4 BE]
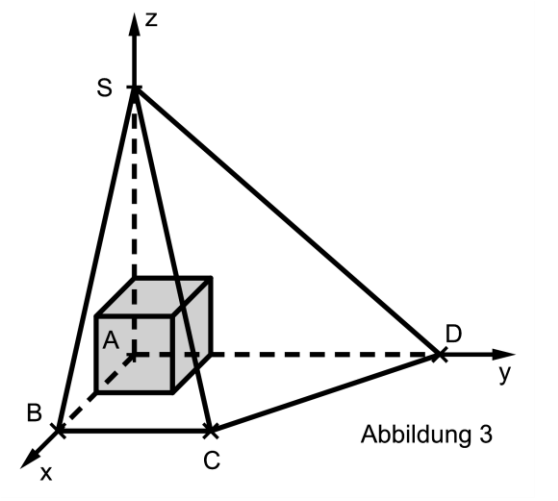
Betrachtet werden die Würfel, von denen drei Seitenflächen in den drei Koordinatenebenen liegen.
Abbildung 3 zeigt einen dieser Würfel.
Unter diesen Würfeln gibt es einen, bei dem ein Eckpunkt auf der Kante der Pyramide liegt.
Berechnen Sie die Kantenlänge dieses Würfels und begründen Sie, dass kein Punkt dieses Würfels außerhalb der Pyramide liegt. [5 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen