Teil 1, Stochastik

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
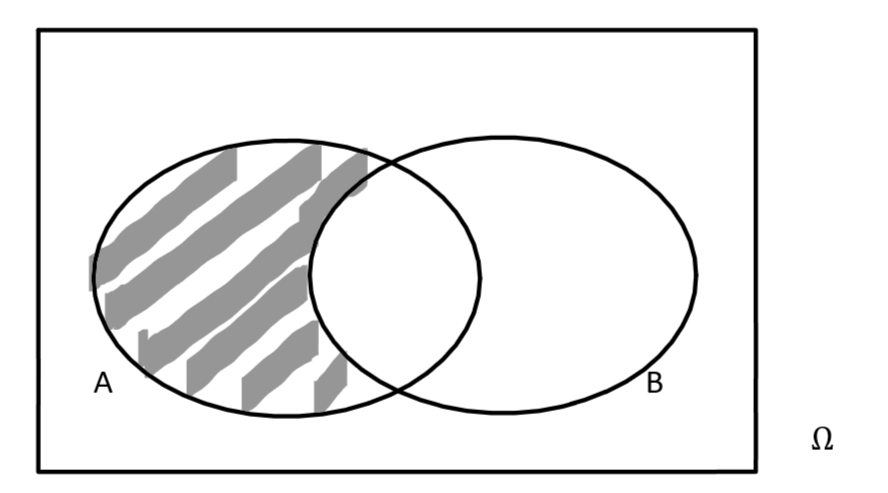
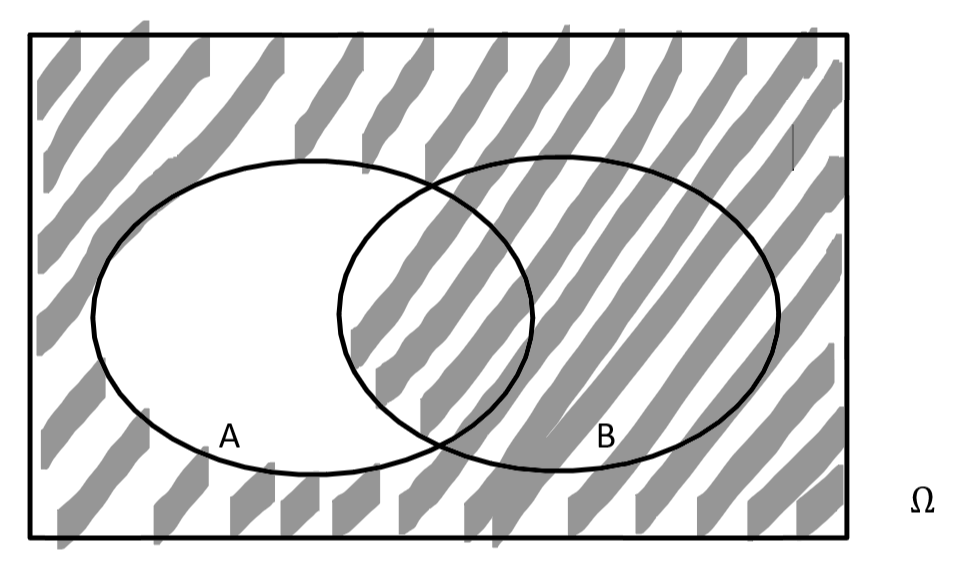
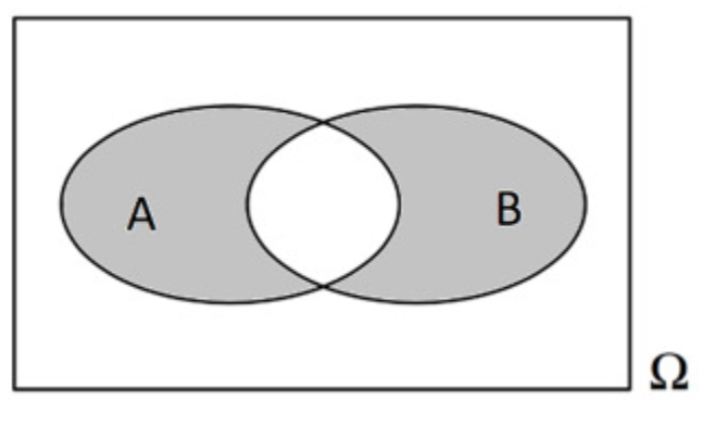
A und B sind zwei beliebige (vereinbare) Ereignisse von $\Omega$ . Geben Sie das in nebenstehenden Venn-Diagramm grau hinterlegte Ereignis $E_{1}$ in möglichst einfacher Symbolschreibweise an und veranschaulichen Sie das Ereignis $E_2=\overline{A\cap\overline B}$ in einem Venn-Diagramm
Für diese Aufgabe benötigst Du folgendes Grundwissen: Venn-Diagramm
Ereignis angeben
Bei $A\cup B$ wäre die Mitte zwischen den beiden Mengen auch ausgemalt.
Bei $A\cap B$ wäre nur die Mitte ausgemalt.
Man muss also von $A\cup B$ die Menge $A\cap B$ wegnehmen: $E_1=(A\cup B)\backslash (A\cap B)$
Venn Diagramm zeichnen
Die Menge $A\cap \overline B$ erhältst du, in dem du den Bereich ausmalst, der sowohl zu A gehört als auch nicht zu B:
Gesucht ist aber genau das Gegenteil dieser Menge. Es muss also alles andere ausgemalt werden. Vergiss nicht, auch den Bereich außerhalb der Menge B auszumalen!
Ereignis angeben:
Überlege dir, wie du das Ereignis mit den Grundoperationen $A\cap B$ und $A\cup B$ erzeugen könntest. Was müsstest du von was wegnehmen?
Verwende das Symbol \ für "ohne", um die Menge zu erzeugen
Venn-Diagramm zeichnen:
Überlege dir zuerst, wie $A\cup \overline B$ aussieht
Markiere genau das Gegenteil davon

Folgendes Baumdiagramm stellt die Ergebnisse eines zweistufigen Zufallsexperiments dar. Dabei gilt: $p\in \mathbb R$ und $0\leq p\leq 1$ .

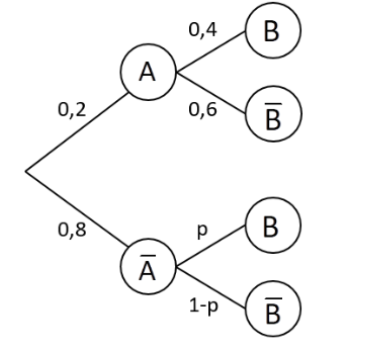
Bestimmen Sie den Wert von p so, dass für die Wahrscheinlichkeit des Ereignisses B gilt: $P (B) = 0, 24$ .

Das zweistufige Zufallsexperiment ist ein Gewinnspiel, bei dem man nur gewinnt, wenn das Ereignis $\overline A\cap\overline B$ eintritt.
Interpretieren Sie folgende Gleichung im Sachzusammenhang:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregeln
linke Seite der Gleichung
Der Term $0{,}8\cdot (1-p)$ beschreibt, wie in der Aufgabenstellung bereits vorgegeben, das Ereignis $\overline A \cap \overline B$ , also es darf weder A noch B eintreten.
Mit dem Exponenten $(. . .)^{3}$ wird ausgedrückt, dass das Ereignis dreimal hintereinander bei drei Versuchen eintreten soll.
rechte Seite der Gleichung und Interpretation
Durch die 0,001 ist die Wahrscheinlichkeit vorgegebn, dass man bei dreimaligem Spielen immer gewinnt.
Mithilfe der Gleichung kann der Wert von p also so bestimmt werden, dass man bei dreimaligem Spielen theoretisch in 0,1% der Fällen jedes Mal gewinnt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Interpretieren bedeutet, dass eine Textantwort gefordert ist.
Überlege, welches Ereignis der Term auf der linken Seite beschreibt. Woher kommt die 0,8? Was ist (1-p)? Warum hoch 3?
Wenn du das Ereignis hast, ist die nächste Frage, was das Gleichsetzen mit 0,001 bedeutet. Irgendwas wird hier festgelegt?

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Auf einem Schulfest wird als Gewinnspiel Dosenwerfen angeboten. Aus den Vorjahren weiß man, dass nur 10% der Teilnehmer es schaffen, alle Dosen abzuräumen und somit einen Gewinn zu erhalten. Betrachtet werden nun sieben zufällig ausgewählte, aufeinanderfolgende Teilnehmer.
Geben Sie jeweils einen Term an, mit dem die Wahrscheinlichkeit folgender Ereignisse berechnet werden kann.
$E_{1}$ : "Die letzten beiden Teilnehmer gewinnen."
$E_{2}$ : "Gewinner und Verlierer wechseln sich ab."
$E_{3}$ : "Genau drei Teilnehmer gewinnen und diese folgen aufeinander."

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
Aufgrund der Aufgabenstellung musst du die Termwerte nicht berechnen!
$E_{1}$
Im Satz steht nicht, dass nur die letzten zwei Teilnehmer gewinnen. Bei den ersten 8 Personen kann also alles passieren, weshalb sie nicht beachtet werden müssen.
Deshalb musst du nur die zwei Gewinner angeben mit der Gewinnwahrscheinlichkeit und der Anzahl 2:
$P(E_1)=0{,}1^2$
$E_{2}$
Insgesamt verlieren 4 Personen und 3 gewinnen oder 4 gewinnen und 3 verlieren. Es gibt dafür also zwei Möglichkeiten: Entweder gewinnt die erste Person (und die zweite verliert, die dritte gewinnt,...) oder es verliert die erste Person (und die zweite gewinnt, die dritte verliert...).
$P(E_2)= 0{,}1^4\cdot 0{,}9^3+0{,}1^3\cdot 0{,}9^4$
$E_{3}$
Es gibt diesmal drei Gewinner und vier Verlierer, deshalb benötigst du auf jeden Fall schon mal die Bestandteile $0{,}1^3$ und $0{,}9^4$ .
Durch Ausprobieren oder durch die Formel n-k+1 mit $n = 7$ Personen und $k = 3$ Gewinner die Anzahl der Möglichkeiten: $7 - 3 + 1 = 5$
Insgesamt also:
$P(E_3)=5\cdot 0{,}1^3\cdot 0{,}9^4$
Bei jedem der drei Ereignisse muss die Wahrscheinlichkeit $p = 0, 1$ für einen Volltreffer und die Gegenwahrscheinlichkeit $q = 0, 9$ mit den korrekten Exponenten versehen werden, z.B. $0{,}1^2$ bei zwei Treffern.
Außerdem muss aber noch überlegt werden, wie viele Möglichkeiten es für dieses Ereignis gibt und diese Zahl mit der Wahrscheinlichkeit multipliziert werden.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle P\left(B\right)$	$=$	$\displaystyle P\left(A\cap B\right)+P\left(\overline{A}\cap B\right)$
	↓	linke Seite aus Angabe, rechte Seite von oben
$\displaystyle 0{,}24$	$=$	$\displaystyle 0{,}08+0{,}8p$	$\displaystyle -0{,}08$
$\displaystyle 0{,}16$	$=$	$\displaystyle 0{,}8p$	$\displaystyle :0{,}8$
$\displaystyle 0{,}2$	$=$	$\displaystyle p$

Teil 1, Stochastik

Ereignis angeben

Venn Diagramm zeichnen

P(B) als Summe zweier Pfadwahrscheinlichkeiten

Pfadwahrscheinlichkeit mit 1. Pfadregel

Gleichung lösen

Hast du eine Frage oder Feedback?

linke Seite der Gleichung

rechte Seite der Gleichung und Interpretation

Hast du eine Frage oder Feedback?

$E_{1}$

$E_{2}$

$E_{3}$

Teil 1, Stochastik

Ereignis angeben

Venn Diagramm zeichnen

P(B) als Summe zweier Pfadwahrscheinlichkeiten

Pfadwahrscheinlichkeit mit 1. Pfadregel

Gleichung lösen

Hast du eine Frage oder Feedback?

linke Seite der Gleichung

rechte Seite der Gleichung und Interpretation

Hast du eine Frage oder Feedback?

E1 E_1E1​

E2E_2E2​

E3E_3E3​

$E_{1}$

$E_{2}$

$E_{3}$