Nachtermin Teil B - lernen mit Serlo!

Aufgabe B 2

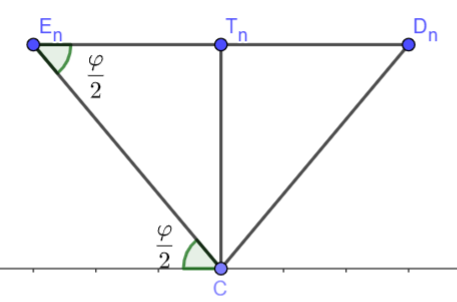
Kongruente, gleichschenklige Dreiecke $A_{n} B_{n} C$ und $C D_{n} E_{n}$ besitzen den gemeinsamen Punkt $C$ . Diese Dreiecke haben die Basen $A_{n} B_{n}$ und $D_{n} E_{n}$ mit den Mittelpunkten $S_{n}$ und $T_{n}$ .

Es gilt: $| A_{n} B_{n} | = | D_{n} E_{n} | = 6 cm$ .

Die Winkel $E_{n} C A_{n}$ und $B_{n} C D_{n}$ haben jeweils das Maß $φ$ mit $φ \in] 0^{\circ}; 180^{\circ} [$ .

Die nebenstehende Skizze zeigt die Dreiecke $A_{1} B_{1} C$ und $C D_{1} E_{1}$ für $φ = 100^{\circ}$ .

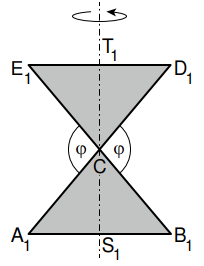
Die Dreiecke $A_{n} B_{n} C$ und $C D_{n} E_{n}$ rotieren um die Gerade $S_{n} T_{n}$ . In der Skizze ist der Axialschnitt des für $φ = 100^{\circ}$ entstehenden Rotationskörpers grau eingefärbt.
Berechnen Sie die Länge der Strecken $C T_{n}$ sowie das Volumen der entstehenden Rotationskörper in Abhängigkeit von $φ$ .
$[$ Ergebnisse: $| C T_{n} | (φ) = 3 \cdot \tan (\frac{φ}{2}) cm$ ; $V (φ) = 18 \cdot π \cdot \tan (\frac{φ}{2}) {cm}^{3}]$ (2,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
Berechne die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$
Die Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur zur Veranschaulichung.
Im oberen Dreieck gilt:
$\tan (\frac{φ}{2}) = \frac{| C T_{n} |}{| E_{n} T_{n} |}$
Dabei ist $| E_{n} T_{n} | = 0,5 \cdot | D_{n} E_{n} | = 0,5 \cdot 6 = 3 cm$ .
$\Rightarrow | C T_{n} | (φ) = | E_{n} T_{n} | \cdot \tan (\frac{φ}{2}) = 3 \cdot \tan (\frac{φ}{2}) cm$
Die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$ lautet:
$| C T_{n} | (φ) = 3 \cdot \tan (\frac{φ}{2}) cm$
Berechne das Volumen des zugehörigen Rotationskörpers
$V = 2 \cdot V_{Kegel}$
$V_{Kegel} = \frac{1}{3} \cdot G \cdot h$
Die Grundfläche ist ein Kreis $G = π \cdot r^{2}$ mit $r = 3 cm$ und $h = | C T_{n} | (φ)$ .
Dann folgt für das gesuchte Volumen:
$V (φ) = 2 \cdot \frac{1}{3} \cdot π \cdot 3^{2} \cdot 3 \cdot \tan (\frac{φ}{2}) = 18 \cdot π \cdot \tan (\frac{φ}{2}) {cm}^{3}$
Das Volumen des zugehörigen Rotationskörpers ist $V (φ) = 18 \cdot π \cdot \tan (\frac{φ}{2}) {cm}^{3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne $\tan (\frac{φ}{2})$ und löse nach $| C T_{n} |$ auf.
Teil 2
Es ist $V = 2 \cdot V_{Kegel}$ mit $V_{Kegel} = \frac{1}{3} \cdot G \cdot h$ .
Die Grundfläche ist ein Kreis und die Höhe $h$ ist $h = | C T_{n} | (φ)$ .
Die Dreiecke $A_{2} B_{2} C$ und $C D_{2} E_{2}$ sind gleichseitig.
Berechnen Sie das Volumen des zugehörigen Rotationskörpers.
Runden Sie auf zwei Stellen nach dem Komma. (1,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
Bekannt ist, dass die Dreiecke $A_{2} B_{2} C$ und $C D_{2} E_{2}$ gleichseitig sind.
Für den Winkel gilt dann:
$\frac{φ}{2} = 60^{\circ} \Rightarrow φ = 120^{\circ}$
$\Rightarrow V (120^{\circ}) = 18 \cdot π \cdot \tan (\frac{120^{\circ}}{2}) \approx 97,95$
Das Volumen des zugehörigen Rotationskörpers beträgt rund $97,95 {cm}^{3}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Beachte, dass im gleichseitigen Dreieck alle Winkel gleich $60^{\circ}$ sind.
Berechne $V (120^{\circ})$ .

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Aufgabe B 2

Berechne die Länge der Strecken CTn in Abhängigkeit von φ

Berechne das Volumen des zugehörigen Rotationskörpers

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechne die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$