Heft 1
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen des Mathe ESA 2021 Prüfungsteil 1.
Ein Taschenrechner ist in diesem Prüfungsteil nicht erlaubt.
- 1
- 2
- 3
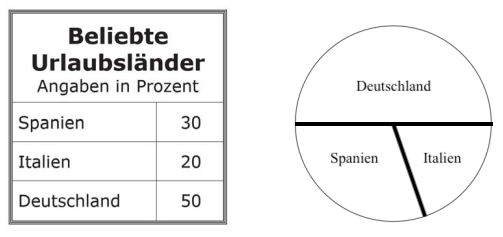
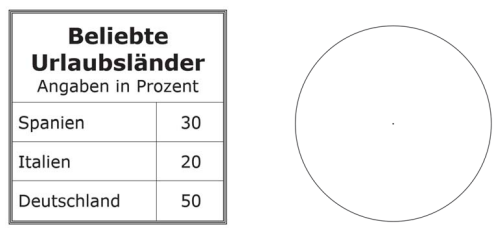
Stelle die Angaben der Umfrage in einem Kreisdiagramm dar. \2P.
- 4
Wie viele Zahlen liegen zwischen 3,4 und 3,6? \1P.
- 5
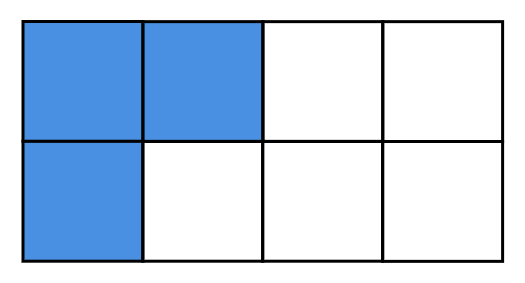
Stelle den Bruch mit einer Zeichnung dar. \1P.
- 6
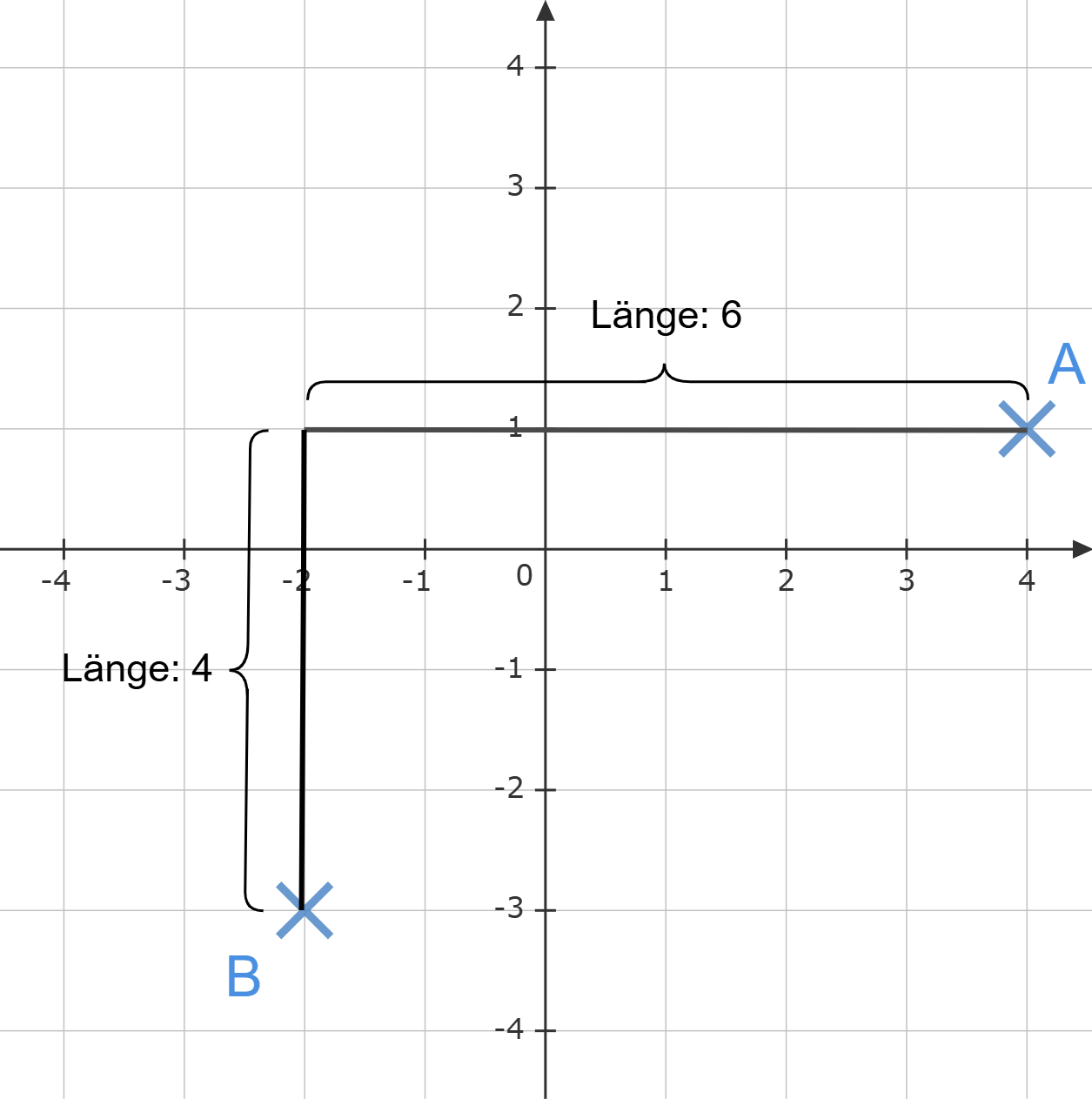
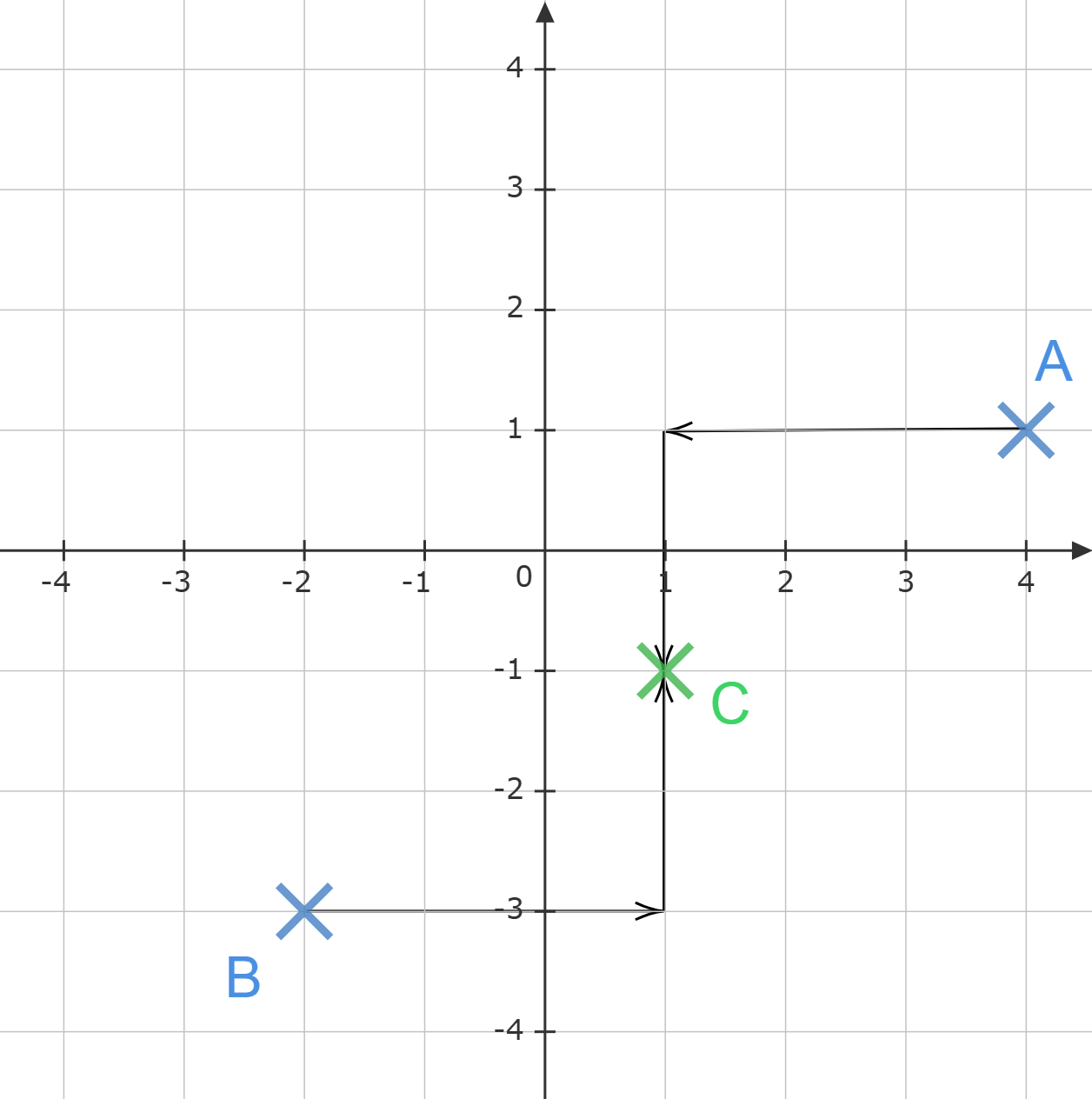
Gib die Koordinaten eines Punktes an, der zu den Punkten und
den gleichen Abstand hat.
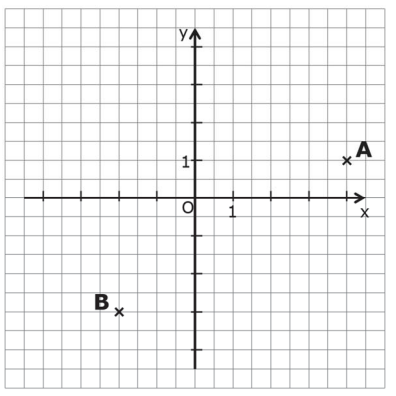
Koordinaten des Punktes C (___|___). \1P.
- 7
Der Körper lässt sich in einen Würfel und eine quadratische Pyramide zerlegen.
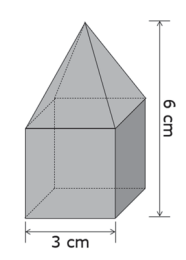
Das Volumen des Körpers beträgt insgesamt
- 8
Die Wertetabelle stellt eine Zuordnung dar.
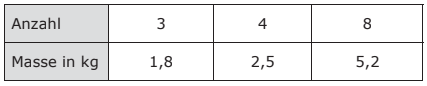
Kreuze an. \1P.
- 9
Eine der Aussagen passt zu der folgenden Rechnung.
Kreuze an. \1P.
- 10
Emil behauptet: „Ein Rechteck mit einem Flächeninhalt von hat auch immer einen Umfang von .“
Zeige durch ein Gegenbeispiel, dass Emil nicht recht hat. \1P.
- 11
- 12
Der Flaschencontainer hat eine kreisrunde Grundfläche.
Kreuze das ungefähre Volumen in Litern an. \1P.

- 13
Bianca baut Würfelgebäude.
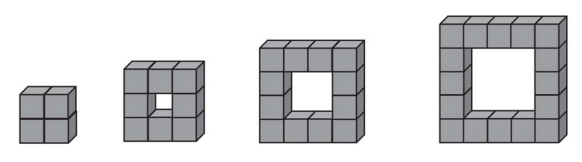
Gib an, aus wie vielen Würfeln das nächstgrößere Würfelgebäude
besteht.
\1P.
Bianca sagt: „Wenn eine Kante des Würfelgebäudes aus 6 Würfeln besteht, rechne ich , um die Anzahl der benötigten Würfel zu bestimmen.“
Erkläre, warum sie so rechnen kann. \1P.
- 14
Ein Spielwürfel ist mit den Zahlen und beschriftet. Gegenüberliegende Flächen haben die gleiche Zahl.
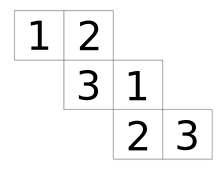
Trage die Zahlen im Würfelnetz ein. \1P.
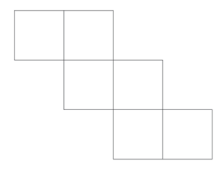
- 15
Bei einem Glücksspielautomaten gewinnt man, wenn die gleichen
Symbole in der gleichen Farbe angezeigt werden.

Die Wahrscheinlichkeit zu gewinnen, ist .
Eine der folgenden Aussagen ist richtig. Kreuze an.
/1P.
Oke soll aus den gegebenen Karten eine ziehen.
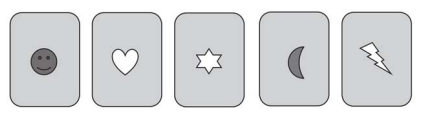
Formuliere eine Spielregel für das Ziehen einer Karte, so dass die
Gewinnchance größer als ist.
/1P.
- 16
Christian berechnet die fehlende Seitenlänge im rechtwinkligen Dreieck.
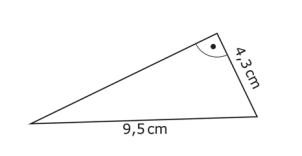
Die Seite ist lang.
Erkläre, warum man am Ergebnis erkennt, dass die Lösung nicht stimmen kann. \1p.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?