Heft 2 - B1
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen des Mathe ESA 2021 Prüfungsteil 2 Aufgabe 1.
Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.
- 1
Biathlon ist eine Wintersportart, bei der die Sportlerinnen und Sportler auf Skiern einen Rundkurs laufen und mit einem Gewehr auf Scheiben schießen. Beim Schießen zielen die Sportler im Liegen und im Stehen je zweimal auf unterschiedlich große Scheiben.
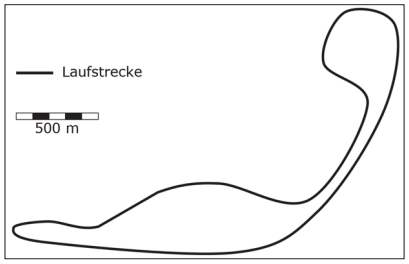
Gib die ungefähre Länge der Strecke in Metern an. \1P.
- 2
Das Diagramm zeigt das Höhenprofil einer Biathlonstrecke.
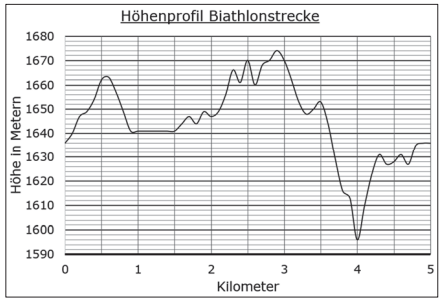
Bestimme den Unterschied zwischen dem höchsten und dem niedrigsten Punkt der Biathlonstrecke in Metern. \2P.
- 3
Beim Schießen muss im Liegen die kleine Scheibe getroffen werden und im
Stehen die große Scheibe.
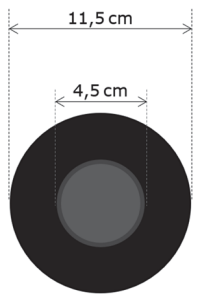
Oke vergleicht die Größe der Flächeninhalte der beiden Scheiben und rechnet:
Er behauptet: „Der Flächeninhalt der großen Scheibe ist ungefähr -mal größer als der
Flächeninhalt der kleinen Scheibe.“
Überprüfe, ob Oke recht hat. \3P.
- 4
Bei einem Rennen über vier Runden müssen die Sportler in jeder Runde auf
fünf schwarze Scheiben schießen.
Bei einem Treffer werden die Scheiben weiß.
Das Beispiel zeigt drei Treffer nach fünf Schüssen.

Ein Sportler trifft durchschnittlich Prozent der Scheiben. Die folgende Abbildung zeigt das Trefferbild des Sportlers im Wettkampf nach insgesamt Schüssen.
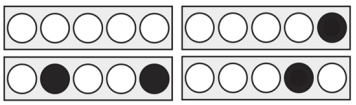
Überprüfe, ob die Trefferquote über dem Durchschnitt liegt. \3P.
- 5
Die Abbildung zeigt die Seitenansicht einer Tribüne sowie eines einzelnen
Sitzes.
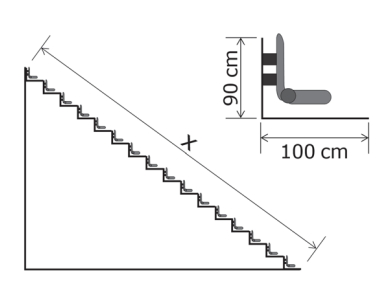
Max berechnet die Länge der Strecke mithilfe der folgenden richtigen
Gleichung:
Gib mithilfe der Gleichung die Länge der Strecke in Metern an. \1P.
Erkläre, warum Max diese Gleichung zur Berechnung nutzen kann. \2P.
- 6
Wahlteil zu B1
Du musst einen der beiden Wahlteile bearbeiten.
Um einen Biathlon-Wettkampf zu sehen, können die Zuschauer zwischen verschiedenen Tribünen wählen.
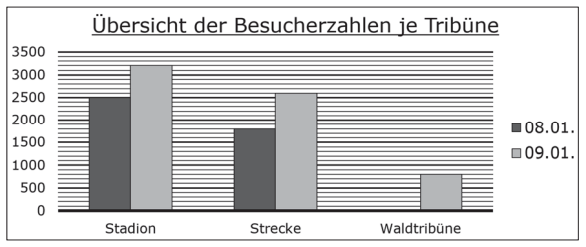
Gib an, wie viele Besucher insgesamt am 09.01. den Biathlon-Wettkampf gesehen haben.
\1P.
Die Tabelle zeigt die Preise für die Eintrittskarten an den beiden Tagen.
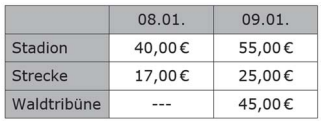
Berechne, wie viele Euro am 08.01. insgesamt durch den Verkauf der Eintrittskarten eingenommen wurde. \2P.
Michelle behauptet: „Im Stadion waren am 09.01. 28 Prozent mehr Zuschauer als am 08.01.“
Überprüfe, ob Michelle recht hat. \3P.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
