Prüfungsteil 2 2024
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Aufgaben mit Hilfsmitteln
Für diese Aufgaben stehen dir in der Zentralen Prüfung 90 Minuten Bearbeitungszeit zur Verfügung. Taschenrechner und Formelsammlung sind für diesen Prüfungsteil erlaubt.
- 1
Fruchtfliegen
Jasmin möchte für ein Biologieprojekt untersuchen, wie schnell sich Fruchtfliegen (Abbildung 1) vermehren. Sie kauft dazu zwei Zuchtboxen und bezeichnet diese mit und .

Zuchtbox A enthält anfänglich zehn Fruchtfliegen. Jasmin bewahrt die Box in ihrem warmen Zimmer auf und protokolliert in den folgenden Tagen die Anzahl der Tiere in der
Box (Abbildung 2).
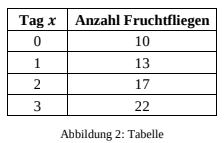
Die Anzahl der Fruchtfliegen in Zuchtbox wächst täglich um ca. %.
Weise dies für den Übergang von Tag 0 auf Tag 1 nach.
Jasmin stellt die Funktion mit der Funktionsgleichung auf, um die Anzahl der Fruchtfliegen am Tag zu berechnen.
Bestimme die voraussichtliche Anzahl an Fruchtfliegen nach 30 Tagen.
Bestimme, nach wie vielen Tagen die Anzahl der Fruchtfliegen erstmals größer als sein müsste.
Zuchtbox enthält anfänglich 20 Fruchtfliegen (). Zur Berechnung der Anzahl der Fruchtfliegen in der Box an Tag x nutzt Jasmin daher die Funktion mit
Jasmin bewahrt die Zuchtbox B im kühleren Keller auf und stellt fest, dass sich die Fruchtfliegen dort langsamer vermehren als in ihrem warmen Zimmer. An Tag 11 sind es 77 Fliegen. Weise rechnerisch nach, dass beträgt.
Jasmin vermutet: „Bei Zuchtbox kommen in der zweiten Woche mehr als doppelt so viele Fruchtfliegen hinzu, als in der ersten Woche hinzugekommen sind.“
Überprüfe ihre Vermutung mit einer Rechnung.
In Abbildung 3 sind die Graphen und dargestellt.
Begründe, dass
(1) die Funktion mit durch Graph dargestellt wird und
(2) die Funktion mit durch Graph dargestellt wird.
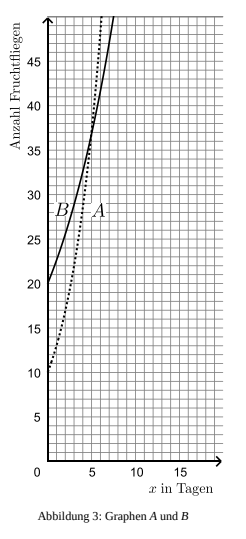
Bestimme mithilfe von Abbildung 3 den Tag, an dem die Zuchtboxen und etwa gleich viele Fruchtfliegen enthalten und gib die Anzahl an.
- 2
Lautsprecher
Chris möchte sich einen Lautsprecher kaufen. Er vergleicht dazu Maße und Volumen des zylinderförmigen Modells Echo mit den Maßen und dem Volumen des näherungsweise kugelförmigen Modells Dot (Abbildung 1).

Das Volumen des zylinderförmigen Modells Echo beträgt ca. .
Berechne die Höhe des Lautsprechers.
Als Näherungslösung berechnet Chris für das Modell Dot das Kugelvolumen. Als Ergebnis erhält er ca. .
Bestätige durch eine Rechnung das Kugelvolumen.
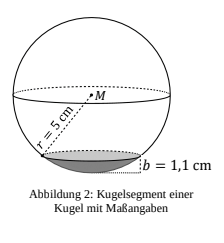
Damit das Modell Dot stabil steht, hat der Hersteller unten ein Kugelsegment abgetrennt. Das Volumen des abgetrennten
Kugelsegments (Abbildung 2) wird mit folgender Formel berechnet:
ist die Höhe des abgetrennten Kugelsegments und der Radius der Kugel.
Bestätige mit einer Rechnung, dass das Volumen des abgetrennten Kugelsegments ca.
% des Kugelvolumens entspricht.
Chris hat sich das Modell Dot gekauft und erstellt eine Playlist mit Liedern seiner drei Lieblingskünstler (Abbildung 3).
Die Lieder der Playlist lässt er in zufälliger Reihenfolge abspielen.
Erläutere, dass die Wahrscheinlichkeit, als erstes ein Lied des Sängers Ed Sheeran zu hören, beträgt.

Bei der zufälligen Wiedergabe wird aus der Playlist jedes Lied nur genau einmal abgespielt.
Von einer Künstlerin/einem Künstler können aber mehrere Lieder nacheinander gespielt werden. Das Baumdiagramm
in Abbildung 4 stellt das Abspielen der ersten beiden Lieder dar.
Ergänze die sechs fehlenden Wahrscheinlichkeiten im Baumdiagramm.
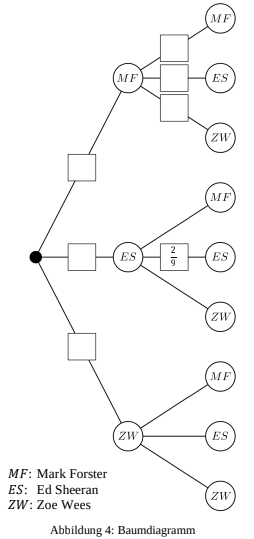
Berechne die Wahrscheinlichkeit, dass die beiden ersten Lieder von Ed Sheeran stammen.
- 3
Dreieck
Abbildung 1 zeigt das Dreieck mit
vorgegebenen Maßangaben.
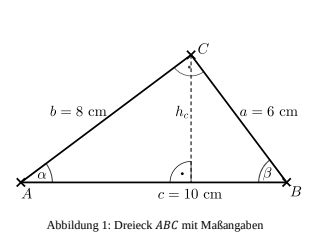
Begründe mithilfe einer Rechnung, dass das Dreieck beim Punkt einen rechten
Winkel hat.
Zeige rechnerisch, dass der Flächeninhalt dieses Dreiecks groß ist.
Begründe, dass die folgende Gleichung gilt:
Bestimme rechnerisch die Länge der Strecke .
Bestimme rechnerisch die Größe des Winkels .
Gegeben ist ein gleichschenkliges rechtwinkliges Dreieck mit der Basis und den beiden Schenkeln und .
(1) Skizziere eine geeignete Planfigur.
(2) Berechne die Länge der Schenkel.
Kai behauptet: „Es gibt auch ein rechtwinkliges Dreieck, bei dem alle drei Seiten gleich lang sind.“
Entscheide begründet, ob Kais Behauptung stimmt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


