Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

B3 Aufgabe 1

Der in Abbildung 1 dargestellte Körper KK mit den Eckpunkten A1,A2,A3,A4,B1,B2,B3A_{1}, A_{2}, A_{3}, A_{4}, B_{1}, B_{2}, B_{3} und B4B_{4} hat folgende Eigenschaften:

A1A2A3A4A_{1} A_{2} A_{3} A_{4} ist ein Rechteck in der x1x2x_{1} x_{2}-Ebene, B1B2B3B4B_{1} B_{2} B_{3} B_{4} ist ein Rechteck in einer zur x1x2x_{1} x_{2}-Ebene parallelen Ebene. Die Vierecke A2A3B3B2A_{2} A_{3} B_{3} B_{2} und A1A4B4B1A_{1} A_{4} B_{4} B_{1} liegen in Ebenen, die parallel zur x1x3x_{1} x_{3}-Ebene verlaufen.

Sechs der Eckpunkte sind gegeben durch

A1(50∣−5∣0)A_{1}(50|-5| 0), A2(50∣5∣0)A_{2}(50|5| 0), A3(753∣5∣0)A_{3}\left(\frac{\sqrt{75}}{3}|5| 0\right), A4(753∣−5∣0)A_{4}\left(\frac{\sqrt{75}}{3}|-5| 0\right), B2(10∣5∣30)B_{2}(10|5| 30), B3(753∣5∣30)B_{3}\left(\frac{\sqrt{75}}{3}|5| 30\right).

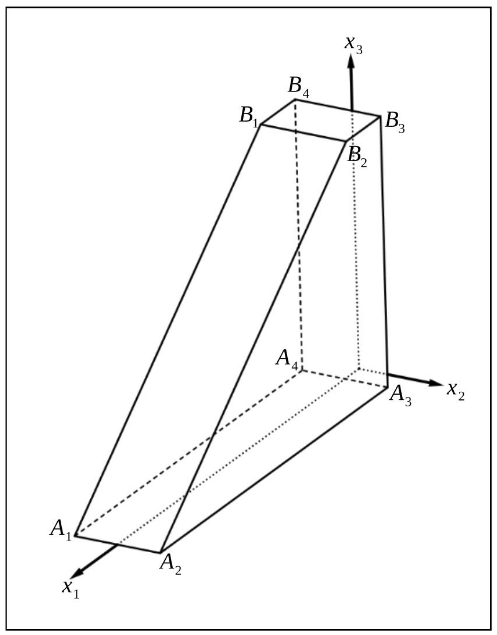
Abbildung 1

Abbildung 1

  1. Geben Sie die Koordinaten des Punktes B1B_{1} an. (1 P)

  2. Begründen Sie, dass die Seitenfläche A2A3B3B2A_{2} A_{3} B_{3} B_{2} ein Trapez ist, und berechnen Sie das Volumen des Körpers KK. (2 P + 2 P)

  3. Berechnen Sie den Winkel zwischen A2A3‾\overline{A_{2} A_{3}} und A2B2‾\overline{A_{2} B_{2}}. (2 P)