A1

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben sind die in $ℝ$ definierten ganzrationalen Funktionen $f_{k}$ mit
$f_{k} (x) = x^{4} + (2 - k) \cdot x^{3} - k \cdot x^{2} mit k \in ℝ$ .
1. Begründen Sie, dass der Graph von $f_{2}$ symmetrisch bezüglich der y-Achse ist. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
  Begründe, dass der Graph von $f_{2}$ symmetrisch bezüglich der y-Achse ist
  Es ist $f_{2} (x) = x^{4} + (2 - 2) \cdot x^{3} - 2 \cdot x^{2} = x^{4} - 2 x^{2}$ .
  Der Funktionsterm von $f_{2}$ enthält nur Potenzen von $x$ mit geraden Exponenten, d.h. der Graph von $f_{2}$ ist symmetrisch zur y-Achse
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Notiere $f_{2} (x)$ und schau Dir die Exponenten an.
2. Es gibt einen Wert von $k$ , für den $x = 1$ eine Wendestelle von $f_{k}$ ist.
  Berechnen Sie diesen Wert von $k$ . (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Berechne diesen Wert von $k$
  Gegeben ist $f_{k} (x) = x^{4} + (2 - k) \cdot x^{3} - k \cdot x^{2}$ .
  Berechne die 1. und 2. Ableitung:
  $f_{k}^{'} (x) = 4 x^{3} + 3 \cdot (2 - k) \cdot x^{2} - 2 k x$
  $f_{k}^{''} (x) = 12 x^{2} + 2 \cdot 3 \cdot (2 - k) \cdot x - 2 k$
  Bekannt ist: Es gibt einen Wert von $k$ , für den $x = 1$ eine Wendestelle von $f_{k}$ ist.
  Demnach muss $f_{k}^{''} (1) = 0$ sein.
  $\Rightarrow f_{k}^{''} (1) = 12 + 6 \cdot (2 - k) - 2 k = 0 \Rightarrow 24 - 6 k - 2 k = 0 \Rightarrow 24 - 8 k = 0$
  $\Rightarrow k = 3$
  Der Wert von $k$ ist gleich $3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die 1. und 2. Ableitung von $f_{k} (x)$ .
  Bekannt ist: Es gibt einen Wert von $k$ , für den $x = 1$ eine Wendestelle von $f_{k}$ ist.
  Demnach muss $f_{k}^{''} (1) = 0$ sein.
  Löse die Gleichung nach $k$ auf.
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Eine Funktionenschar $f_{k}$ ist gegeben durch die Gleichung
$f_{k} (x) = \frac{1}{k} \cdot x \cdot e^{- k^{2} \cdot x}, x \in ℝ, k \in ℝ, k \neq 0$ .
1. Zeigen Sie rechnerisch: $f_{k}^{'} (x) = (- k \cdot x + \frac{1}{k}) \cdot e^{- k^{2} \cdot x}$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
  Zeige rechnerisch: $f_{k}^{'} (x) = (- k \cdot x + \frac{1}{k}) \cdot e^{- k^{2} \cdot x}$
  Gegeben ist $f_{k} (x) = \frac{1}{k} \cdot x \cdot e^{- k^{2} \cdot x}$ .
  Mit der Produkt- und Kettenregel folgt:
  $f_{k}^{'} (x) = \frac{1}{k} (1 \cdot e^{- k^{2} \cdot x} + x (- k^{2}) \cdot e^{- k^{2} \cdot x})$
  $f_{k}^{'} (x) = \frac{1}{k} \cdot e^{- k^{2} \cdot x} (1 - k^{2} x) = (- k x + \frac{1}{k}) \cdot e^{- k^{2} \cdot x}$
  Also ist $f_{k}^{'} (x) = (- k x + \frac{1}{k}) \cdot e^{- k^{2} \cdot x}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die 1. Ableitung mit der Produkt- und Kettenregel.
2. Im Folgenden können Sie verwenden: $f_{k}^{''} (\frac{1}{k^{2}}) = - k \cdot e^{- 1}$ .
  Zeigen Sie, dass $\frac{1}{k^{2}}$ eine Extremstelle aller Funktionen der Schar ist, und untersuchen Sie, für welche Werte von $k$ die Funktionen der Schar an der Stelle $\frac{1}{k^{2}}$ ein Minimum besitzen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Zeige, dass $\frac{1}{k^{2}}$ eine Extremstelle aller Funktionen der Schar ist
  Gegeben ist $f_{k}^{''} (\frac{1}{k^{2}}) = - k \cdot e^{- 1}$ .
  Die notwendige Bedingung für eine Extremstelle bei $x = \frac{1}{k^{2}}$ ist $f_{k}^{'} (\frac{1}{k^{2}}) = 0$ .
  Es ist $f_{k}^{'} = (- k x + \frac{1}{k}) \cdot e^{- k^{2} \cdot x}$ (Aufgabe a).
  Setze $x = \frac{1}{k^{2}}$ ein: $f_{k}^{'} (\frac{1}{k^{2}}) = (- k \cdot \frac{1}{k^{2}} + \frac{1}{k}) \cdot e^{- k^{2} \cdot \frac{1}{k^{2}}} = (- \frac{1}{k} + \frac{1}{k}) \cdot e^{- 1} = 0 \cdot e^{- 1} = 0$ für alle $k \neq 0$ .
  Wegen $f_{k}^{''} (\frac{1}{k^{2}}) = - k \cdot e^{- 1} \neq 0$ für alle $k \neq 0$ ist $\frac{1}{k^{2}}$ eine Extremstelle aller Funktionen der Schar.
  Untersuche, für welche Werte von $k$ die Funktionen der Schar an der Stelle $\frac{1}{k^{2}}$ ein Minimum besitzen
  Für ein Minimum muss $f_{k}^{''} (\frac{1}{k^{2}}) > 0$ sein.
  $\Rightarrow f_{k}^{''} (\frac{1}{k^{2}}) = - k \cdot e^{- 1} > 0 \Leftrightarrow k < 0$ .
  Damit besitzen genau die $f_{k}$ mit $k < 0$ ein Minimum an der Extremstelle $\frac{1}{k^{2}}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Weise nach: Die notwendige Bedingung für eine Extremstelle bei $x = \frac{1}{k^{2}}$ ist $f_{k}^{'} (\frac{1}{k^{2}}) = 0$ . Beachte $f_{k}^{''} (\frac{1}{k^{2}}) = - k \cdot e^{- 1} \neq 0$ .
  Teil 2
  Es ist $f_{k}^{''} (\frac{1}{k^{2}}) = - k \cdot e^{- 1}$ .
  Für ein Minimum muss $f_{k}^{''} (\frac{1}{k^{2}}) > 0$ sein.
  Was folgt daraus für den Wert von $k$ ?
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Gegeben sind die Funktionen $f$ und $h$ mit den Gleichungen
$\begin{aligned} f (x) = (x - 3) \cdot e^{x}, x \in ℝ, \\ h (x) = x - 3, x \in ℝ . \end{aligned}$
1. Bestimmen Sie rechnerisch die beiden Schnittstellen der Graphen der Funktionen $f$ und $h$ .
  $[$ Zur Kontrolle: Die Schnittstellen sind $x = 0$ und $x = 3$ . $]$ (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
  Bestimme rechnerisch die beiden Schnittstellen der Graphen der Funktionen $f$ und $h$
  $f (x) = h (x) \Leftrightarrow (x - 3) \cdot e^{x} = x - 3 \Leftrightarrow (x - 3) \cdot (e^{x} - 1) = 0 \Leftrightarrow x - 3 = 0 \lor e^{x} - 1 = 0 \Leftrightarrow x = 3 \lor x = 0$
  Die Graphen der Funktionen $f$ und $h$ schneiden sich an den Stellen $x = 3$ und $x = 0$ .
  .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Gleichung $f (x) = h (x)$ .
2. Zwischen den Schnittstellen verläuft der Graph von $h$ oberhalb des Graphen von $f$ .
  Die Funktion $D (x) = (4 - x) \cdot e^{x} + 0,5 \cdot x^{2} - 3 \cdot x$ ist eine Stammfunktion der Funktion $d$ mit $d (x) = h (x) - f (x)$ .
  Ermitteln Sie den Flächeninhalt der Fläche, die von den Graphen der Funktionen $h$ und $f$ eingeschlossen wird. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Ermittele den Flächeninhalt der Fläche, die von den Graphen der Funktionen $h$ und $f$ eingeschlossen wird
  Für den Flächeninhalt gilt:
  $\int_{0}^{3} d (x) d x = D (3) - D (0) = ((4 - 3) \cdot e^{3} + 0,5 \cdot 3^{2} - 3 \cdot 3) - 4 \cdot e^{0}$
  $\int_{0}^{3} d (x) d x = e^{3} + 4,5 - 9 - 4 = e^{3} - 8,5$
  Der Flächeninhalt beträgt $(e^{3} - 8,5) FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne mit der Stammfunktion $D (x)$ das Integral $\int_{0}^{3} d (x) d x$ .
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Betrachtet werden die in $ℝ$ definierten Funktionen $f$ und $F$ , wobei $F$ eine Stammfunktion von $f$ ist. Die Abbildung zeigt den Graphen $G_{F}$ von $F$ .
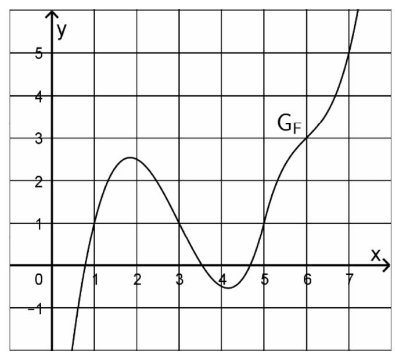
Abbildung
1. Bestimmen Sie den Wert des Integrals $\int_{1}^{7} f (x) d x$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hauptsatz der Differential- und Integralrechnung
  Bestimme den Wert des Integrals $\int_{1}^{7} f (x) d x$
  Die Stammfunktion hat die Funktionswerte (abgelesen aus der Abbildung):
  $F (7) = 5$
  $F (1) = 1$
  Das Integral ist nach dem Hauptsatz der Differential- und Integralrechnung:
  $\int_{1}^{7} f (x) d x$ $=$ $F (7) - F (1)$
  ↓
  Einsetzen
  $=$ $5 - 1$
  $=$ $4$
  Der Wert des Integrals ist gleich $4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies die Funktionswerte $F (7)$ und $F (1)$ aus dem Schaubild ab.
  Bestimme den Wert des Integrals.
2. Bestimmen Sie grafisch näherungsweise den Funktionswert von $f$ an der Stelle $1$ .
  (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hauptsatz der Differential- und Integralrechnung
  Bestimme grafisch näherungsweise den Funktionswert von $f$ an der Stelle $1$
  Laut dem Hauptsatz der Differential- und Integralrechnung gilt:
  Die Ableitung von $F$ ist die Funktion $f$ .
  Der Funktionswert $f (1)$ ist damit die Steigung, die $F$ an der Stelle $x = 1$ hat.
  Mithilfe des Schaubilds gilt: $F^{'} (1) = f (1) \approx \frac{4}{1} = 4$
  Schaubild mit Steigungsdreieck
  Der Funktionswert von $f$ an der Stelle $1$ beträgt ungefähr $4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Funktionswert $f (1)$ ist damit die Steigung, die $F$ an der Stelle $x = 1$ hat.
  Zeichne ein Steigungsdreieck bei $x = 1$ ein und bestimme die Steigung.
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 5
Gegeben sind die Gerade $g : \vec{x} = (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}), r \in ℝ$ und die Ebene $E : \vec{x} = (\begin{array}{l} 0 \\ 1 \\ 4 \end{array}) + s \cdot (\begin{array}{l} 4 \\ 2 \\ 3 \end{array}) + t \cdot (\begin{array}{l} 2 \\ 0 \\ 1 \end{array}), s, t \in ℝ$ .
1. Weisen Sie nach, dass die Gerade $g$ senkrecht zur Ebene $E$ verläuft. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Weise nach, dass die Gerade $g$ senkrecht zur Ebene $E$ verläuft
  Wenn die Gerade $g$ senkrecht zur Ebene $E$ verläuft, dann muss der Richtungsvektor ${\vec{u}}_{g}$ der Geraden $g$ senkrecht zu beiden Richtungsvektoren ${\vec{v}}_{E}$ und ${\vec{w}}_{E}$ der Ebene $E$ verlaufen. Für das Skalarprodukt gilt dann:
  ${\vec{u}}_{g} \circ {\vec{v}}_{g} = 0$ und ${\vec{u}}_{g} \circ {\vec{w}}_{g} = 0$
  $\Rightarrow$ $(\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) \cdot (\begin{array}{l} 4 \\ 2 \\ 3 \end{array}) = 1 \cdot 4 + 1 \cdot 2 + (- 2) \cdot 3 = 0 ✓$
  und
  $(\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) \cdot (\begin{array}{l} 2 \\ 0 \\ 1 \end{array}) = 1 \cdot 2 + 0 - 2 = 0 ✓$
  Somit verläuft $g$ senkrecht zu $E$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechnen Sie die Koordinaten des Schnittpunktes $D$ der Geraden $g$ mit der Ebene $E$ . (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
  Berechne die Koordinaten des Schnittpunktes $D$ der Geraden $g$ mit der Ebene $E$
  Setze $g = E$ :
  $(\begin{array}{c} 2 \\ 1 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) = (\begin{array}{l} 0 \\ 1 \\ 4 \end{array}) + s \cdot (\begin{array}{l} 4 \\ 2 \\ 3 \end{array}) + t \cdot (\begin{array}{l} 2 \\ 0 \\ 1 \end{array})$
  $\Rightarrow (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array}) - (\begin{array}{c} 0 \\ 1 \\ 4 \end{array}) = r \cdot (\begin{array}{l} - 1 \\ - 1 \\ 2 \end{array}) + s \cdot (\begin{array}{l} 4 \\ 2 \\ 3 \end{array}) + t \cdot (\begin{array}{l} 2 \\ 0 \\ 1 \end{array})$
  $\Rightarrow (\begin{array}{c} 2 \\ 0 \\ - 5 \end{array}) = r \cdot (\begin{array}{l} - 1 \\ - 1 \\ 2 \end{array}) + s \cdot (\begin{array}{l} 4 \\ 2 \\ 3 \end{array}) + t \cdot (\begin{array}{l} 2 \\ 0 \\ 1 \end{array})$
  Man erhält dann das folgende Gleichungssystem:
  $\begin{array}{ccccc} I & - 1 \cdot r & + & 4 \cdot s & + & 2 \cdot t & = 2 \\ II & - 1 \cdot r & + & 2 \cdot s & + & 0 \cdot t & = 0 \\ III & 2 \cdot r & + & 3 \cdot s & + & 1 \cdot t & = - 5 \end{array}$
  Aus Gleichung $II$ folgt: $r = 2 s$
  Setze $r = 2 s$ in Gleichung $I$ und $III$ ein:
  $\begin{array}{ccccc} I & - 1 \cdot 2 s & + & 4 \cdot s & + & 2 \cdot t & = 2 \\ III & 2 \cdot 2 s & + & 3 \cdot s & + & 1 \cdot t & = - 5 \end{array}$
  Zusammengefasst folgt:
  $\begin{array}{ccccc} I^{'} & 2 \cdot s & + & 2 \cdot t & = 2 \\ I I I^{'} & 7 \cdot s & + & 1 \cdot t & = - 5 \end{array}$
  Rechne $I^{'} + (- 2) \cdot I I I^{'} :$
  $\begin{array}{rrrrrcrr} I^{'} : & 2 \cdot s & + & 2 \cdot t & = & 2 \\ + (- 2) \cdot I I I^{'} : & - 14 \cdot s & - & 2 \cdot t & = & 10 \\ - 12 \cdot s & + & 0 & = & 12 \end{array}$
  Damit ist $s = \frac{12}{- 12} = - 1$ . Dann folgt $r = 2 \cdot s = 2 \cdot (- 1) = - 2$ und $t = 1 - s = 1 - (- 1) = 2$
  Setze $r = - 2$ in $g$ ein:
  $\vec{O D} = (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array}) + (- 2) \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 0 \\ - 1 \\ 3 \end{array}) \Rightarrow D (0 | - 1 | 3)$
  Die Koordinaten des Schnittpunktes $D$ der Geraden $g$ mit der Ebene $E$ lauten $D (0 | - 1 | 3)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $g = E$ und löse das Gleichungssystem $\Rightarrow r, s, t$ .
  Setze das Berechnete $r$ in $g$ ein $\Rightarrow D$ .
6
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 6
Gegeben sind die Punkte $A (- 5 | 5 | - 3)$ und $B (- 1 | 1 | - 1)$ .
Geben Sie die Koordinaten des Mittelpunktes der Strecke $A B$ an und bestimmen Sie eine Gleichung derjenigen Mittelsenkrechten von $A B$ , die parallel zur $x_{1} x_{3}$ -Ebene verläuft.
(1 P + 4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
Gib die Koordinaten des Mittelpunktes der Strecke $A B$ an
Es ist $\vec{m} = \frac{1}{2} \cdot ((\begin{array}{c} - 5 \\ 5 \\ - 3 \end{array}) + (\begin{array}{c} - 1 \\ 1 \\ - 1 \end{array})) = (\begin{array}{c} - 3 \\ 3 \\ - 2 \end{array}) \Rightarrow M (- 3 | 3 | - 2)$
Die Koordinaten des Mittelpunktes der Strecke $A B$ sind $M (- 3 | 3 | - 2)$ .
Bestimme eine Gleichung derjenigen Mittelsenkrechten von $A B$ , die parallel zur $x_{1} x_{3}$ -Ebene verläuft
Wenn die Gerade parallel zur $x_{1} x_{3}$ -Ebene verläuft, dann ist $x_{2}$ -Koordinate des Richtungsvektors gleich null.
Der Richtungsvektor der Geraden hat dann die allgemeine Form $(\begin{array}{c} a \\ 0 \\ b \end{array})$ und die Gleichung der Mittelsenkrechten ist dann:
$\vec{x} = (\begin{array}{c} - 3 \\ 3 \\ - 2 \end{array}) + s \cdot (\begin{array}{c} a \\ 0 \\ b \end{array})$ mit $s \in ℝ$ .
Der Vektor $\vec{A B}$ wird berechnet:
$\vec{A B} = \vec{O B} - \vec{O A} = (\begin{array}{c} - 1 \\ 1 \\ - 1 \end{array}) - (\begin{array}{c} - 5 \\ 5 \\ - 3 \end{array}) = (\begin{array}{c} 4 \\ - 4 \\ 2 \end{array})$
Der Richtungsvektor der Geraden muss senkrecht auf dem Vektor $\vec{A B}$ stehen, d.h. das Skalarprodukt ist gleich null.
$\Rightarrow \vec{A B} \circ (\begin{array}{l} a \\ 0 \\ b \end{array}) = 0 \Leftrightarrow (\begin{array}{c} 4 \\ - 4 \\ 2 \end{array}) \circ (\begin{array}{l} a \\ 0 \\ b \end{array}) = 0 \Leftrightarrow 4 a + 2 b = 0$ liefert $a = - 1$ und $b = 2$ als geeignete Werte von $a$ und $b$ .
Somit ist $\vec{x} = (\begin{array}{c} - 3 \\ 3 \\ - 2 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 0 \\ 2 \end{array})$ mit $s \in ℝ$ eine Gleichung der gesuchten Mittelsenkrechten.
Teil 1
Berechne $\vec{m} = \frac{1}{2} \cdot (\vec{O A} + \vec{O B})$ .
Teil 2
Der Richtungsvektor der Geraden hat die allgemeine Form $\vec{v} = (\begin{array}{c} a \\ 0 \\ b \end{array})$ und die Gleichung der Mittelsenkrechten ist dann: $\vec{x} = \vec{O M} + s \cdot \vec{v}$ .
Der Richtungsvektor der Geraden $(\begin{array}{c} a \\ 0 \\ b \end{array})$ muss senkrecht auf dem Vektor $\vec{A B}$ stehen, d.h. das Skalarprodukt ist gleich null $\Rightarrow a$ und $b$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\int_{1}^{7} f (x) d x$	$=$	$F (7) - F (1)$
	↓	Einsetzen
	$=$	$5 - 1$
	$=$	$4$

A1

Aufgabe 1

Begründe, dass der Graph von f2 symmetrisch bezüglich der y-Achse ist

Hast du eine Frage oder Feedback?

Berechne diesen Wert von k

Hast du eine Frage oder Feedback?

Aufgabe 2

Zeige rechnerisch: fk′(x)=(−k⋅x+1k)⋅e−k2⋅x

Hast du eine Frage oder Feedback?

Zeige, dass 1k2 eine Extremstelle aller Funktionen der Schar ist

Untersuche, für welche Werte von k die Funktionen der Schar an der Stelle 1k2 ein Minimum besitzen

Hast du eine Frage oder Feedback?

Aufgabe 3

Bestimme rechnerisch die beiden Schnittstellen der Graphen der Funktionen f und h

Hast du eine Frage oder Feedback?

Ermittele den Flächeninhalt der Fläche, die von den Graphen der Funktionen h und f eingeschlossen wird

Hast du eine Frage oder Feedback?

Aufgabe 4

Bestimme den Wert des Integrals ∫17f(x)dx

Hast du eine Frage oder Feedback?

Bestimme grafisch näherungsweise den Funktionswert von f an der Stelle 1

Hast du eine Frage oder Feedback?

Aufgabe 5

Weise nach, dass die Gerade g senkrecht zur Ebene E verläuft

Hast du eine Frage oder Feedback?

Berechne die Koordinaten des Schnittpunktes D der Geraden g mit der Ebene E

Hast du eine Frage oder Feedback?

Aufgabe 6

Gib die Koordinaten des Mittelpunktes der Strecke AB an

Bestimme eine Gleichung derjenigen Mittelsenkrechten von AB, die parallel zur x1x3-Ebene verläuft

Begründe, dass der Graph von $f_{2}$ symmetrisch bezüglich der y-Achse ist

Berechne diesen Wert von $k$

Zeige rechnerisch: $f_{k}^{'} (x) = (- k \cdot x + \frac{1}{k}) \cdot e^{- k^{2} \cdot x}$

Zeige, dass $\frac{1}{k^{2}}$ eine Extremstelle aller Funktionen der Schar ist

Untersuche, für welche Werte von $k$ die Funktionen der Schar an der Stelle $\frac{1}{k^{2}}$ ein Minimum besitzen

Bestimme rechnerisch die beiden Schnittstellen der Graphen der Funktionen $f$ und $h$

Ermittele den Flächeninhalt der Fläche, die von den Graphen der Funktionen $h$ und $f$ eingeschlossen wird

Bestimme den Wert des Integrals $\int_{1}^{7} f (x) d x$

Bestimme grafisch näherungsweise den Funktionswert von $f$ an der Stelle $1$

Weise nach, dass die Gerade $g$ senkrecht zur Ebene $E$ verläuft

Berechne die Koordinaten des Schnittpunktes $D$ der Geraden $g$ mit der Ebene $E$

Gib die Koordinaten des Mittelpunktes der Strecke $A B$ an

Bestimme eine Gleichung derjenigen Mittelsenkrechten von $A B$ , die parallel zur $x_{1} x_{3}$ -Ebene verläuft