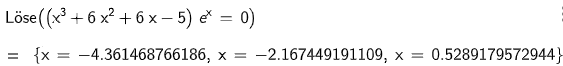B1 - lernen mit Serlo!

Aufgabe 1

Die Funktion $f$ ist gegeben durch die Gleichung

$f (x) = (x^{3} - 5) e^{x}, x \in ℝ$ .

Der Graph von $f$ ist in Abbildung 1 dargestellt.

Im Folgenden darf ohne Nachweis verwendet werden: $f^{'} (x) = (x^{3} + 3 x^{2} - 5) \cdot e^{x}$ .

Zeigen Sie: $f^{''} (x) = (x^{3} + 6 x^{2} + 6 x - 5) \cdot e^{x}$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Gegeben ist $f^{'} (x) = (x^{3} + 3 x^{2} - 5) \cdot e^{x}$ .
Berechne $f^{''} (x)$ mit der Produktregel: $f^{''} (x) = (3 x^{2} + 6 x) \cdot e^{x} + (x^{3} + 3 x^{2} - 5) \cdot e^{x} = (x^{3} + 6 x^{2} + 6 x - 5) \cdot e^{x}$
Damit ist $f^{''} (x) = (x^{3} + 6 x^{2} + 6 x - 5) \cdot e^{x}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $f^{''} (x)$ .
Der Graph von $f$ besitzt genau eine Extremstelle und drei Wendestellen.
Berechnen Sie die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Berechne die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet
Es ist $f^{''} (x) = (x^{3} + 6 x^{2} + 6 x - 5) \cdot e^{x}$ .
Löse die Gleichung $f^{''} (x) = 0$ (notwendige Bedingung).
Die Gleichung hat die Lösungen $x_{W 1}, x_{W 2}$ und $x_{W 3}$ mit $x_{W 1} \approx - 4,361, x_{W 2} \approx - 2,167$ und $x_{W 3} \approx 0,529$ .
Anmerkung: Da die Existenz von drei Wendestellen durch die Aufgabenstellung gesichert ist, ist keine Prüfung eines hinreichenden Kriteriums erforderlich.
Die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet sind
$x_{W 1} \approx - 4,361, x_{W 2} \approx - 2,167$ und $x_{W 3} \approx 0,529$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $f^{''} (x)$ und löse die Gleichung $f^{''} (x) = 0$ (notwendige Bedingung).
Hinweis: Es ist keine Prüfung eines hinreichenden Kriteriums erforderlich.
Für $z > 0$ ist $P_{z} (z | f (z))$ ein Punkt auf dem Graphen von $f$ . Er bildet zusammen mit dem Koordinatenursprung $O (0 | 0)$ und dem Punkt $Q_{z} (z | 0)$ ein Dreieck $O P_{z} Q_{z}$ .
Bestimmen Sie den Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
Bestimme den Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird
Der Taschenrechner liefert für den Tiefpunkt des Graphen von $f$ ungefähr $T P (1,1 | - 11)$ .
Dann erhält man für den Flächeninhalt des Dreiecks:
$A_{Dreieck} = \frac{1}{2} \cdot g \cdot h \approx \frac{1}{2} \cdot 1,1 \cdot 11 = 6,05$ .
Der Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird, beträgt rund $6,05 FE$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Taschenrechner liefert für den Tiefpunkt des Graphen von $f$ ungefähr $T P (x_{1} | y_{1})$ .
Dann ist $A_{Dreieck} \approx \frac{1}{2} \cdot x_{1} \cdot y_{1}$ $[FE]$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 1

Hast du eine Frage oder Feedback?

Berechne die Wendestellen der Funktion f auf drei Nachkommastellen gerundet

Hast du eine Frage oder Feedback?

Bestimme den Flächeninhalt des Dreiecks OPzQz, wenn für Pz der Tiefpunkt des Graphen von f gewählt wird

Hast du eine Frage oder Feedback?

Berechne die Wendestellen der Funktion $f$ auf drei Nachkommastellen gerundet

Bestimme den Flächeninhalt des Dreiecks ${OP}_{z} Q_{z}$ , wenn für $P_{z}$ der Tiefpunkt des Graphen von $f$ gewählt wird