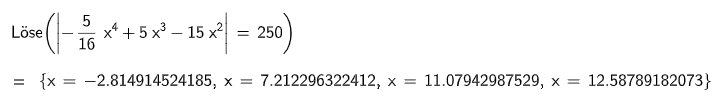B2
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe 1
Die Abbildung zeigt den Graphen der in definierten Funktion mit .
Abbildung
Zeigen Sie rechnerisch, dass der Punkt ein Hochpunkt des Graphen von ist und dass die Tangente an den Graphen von im Punkt parallel zur -Achse verläuft. (5 P)
Bestimmen Sie eine Gleichung der Geraden , die durch die beiden Wendepunkte des Graphen von verläuft.
Zeichnen Sie in die Abbildung eine Gerade ein, die parallel zu ist und für mit dem Graphen von genau einen Punkt gemeinsam hat. (6 P)
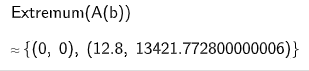
Die Punkte und bilden für jede reelle Zahl mit ein Dreieck .
Ermitteln Sie denjenigen Wert von , für den der Flächeninhalt des Dreiecks maximal wird, und geben Sie diesen Flächeninhalt an.
Hinweis: Eine Betrachtung der Randwerte ist nicht erforderlich. (4 P)
- 2
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist .
Für jede reelle Zahl ist eine in definierte Funktion mit gegeben.
Beschreiben Sie, wie der Graph von aus dem Graphen von erzeugt werden kann.
(2 P)
Bestimmen Sie denjenigen Wert von , für den der Punkt auf dem Graphen von liegt. (2 P)
Die Gleichung hat genau die drei Lösungen und und es gilt .
Erläutern Sie die geometrische Bedeutung dieser Aussage in Bezug auf die Graphen von und . (3 P)
Ermitteln Sie, an welchen Stellen im Intervall die Graphen der Funktionen und einen vertikalen Abstand von Längeneinheiten haben. (4 P)
- 3
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Die Abbildung zeigt den Graphen der in definierten Funktion mit .
Abbildung
Ein Unternehmen lagert Glyzerin in einem Tank. Die momentane Änderungsrate des Tankinhalts kann für mithilfe der Funktion (aus Aufgabe 1) beschrieben werden. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Stunden und die momentane Änderungsrate in Kilogramm pro Stunde. Zu Beobachtungsbeginn befinden sich im Tank Glyzerin.
Der Punkt liegt auf dem Graphen von .
Interpretieren Sie die Koordinaten dieses Punktes im Sachzusammenhang. (2 P)
Beurteilen Sie die folgende Aussage: "Zwölf Stunden nach Beobachtungsbeginn ist die größte Menge Glyzerin im Tank enthalten." (2 P)
Bestimmen Sie die Zunahme des Tankinhalts zwischen den Zeitpunkten acht Stunden und zehn Stunden nach Beobachtungsbeginn. (2 P)
Berechnen Sie, wie viel Glyzerin Stunden nach Beobachtungsbeginn im Tank enthalten ist. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?