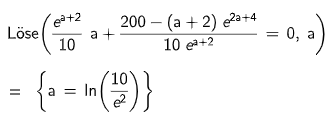B1 - lernen mit Serlo!

Aufgabe 5

Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.

$t_{a}$ ist die Tangente im Wendepunkt $W_{a} (a + 2 | h_{a} (a + 2))$ . Eine Gleichung für $t_{a}$ ist $y = - 10 \cdot e^{- a - 2} \cdot x + 10 (a + 4) \cdot e^{- a - 2}$ .

Weiterhin ist $h_{a} (x) = 10 \cdot (x - a) \cdot e^{- x}, x \in ℝ, a \in ℝ$ .

Die Gerade $l_{a}$ ist die Gerade, die im Wendepunkt $W_{a} (a + 2 | h_{a} (a + 2))$ senkrecht auf der Tangente $t_{a}$ steht.

Ermitteln Sie eine Gleichung für $l_{a}$ . (4 P)
$[$ Mögliche Lösung: $y = \frac{e^{a + 2}}{10} \cdot x + \frac{200 - (a + 2) e^{2 a + 4}}{10 \cdot e^{a + 2}}]$
$[$ Hinweis: Ohne Nachweis kannst du den folgenden Sachverhalt nutzen:
Zwei Geraden stehen senkrecht aufeinander genau dann, wenn für ihre Steigungen gilt: $m_{1} \cdot m_{2} = - 1$ . $]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Normale
Ermittle eine Gleichung für $l_{a}$
Gegeben ist der Wendepunkt $W_{a} (a + 2 | h_{a} (a + 2))$ und die Gleichung der Tangente $t_{a} : y = - 10 \cdot e^{- a - 2} \cdot x + 10 (a + 4) \cdot e^{- a - 2}$ $\Rightarrow m_{t_{a}} = - 10 \cdot e^{- a - 2}$ .
Berechne zunächst $h_{a} (a + 2) = 10 \cdot (a + 2 - a) \cdot e^{- (a + 2)}$ .
$h_{a} (a + 2) = 20 \cdot e^{- a - 2}$
Die Gerade $l_{a}$ ist die Gerade, die im Wendepunkt $W_{a} (a + 2 | h_{a} (a + 2))$ senkrecht auf der Tangente $t_{a}$ steht $\Rightarrow m_{l_{a}} \cdot m_{t_{a}} = - 1 \Rightarrow m_{l_{a}} = - \frac{1}{m_{t_{a}}} = - \frac{1}{- 10 \cdot e^{- a - 2}}$ .
Somit ist $m_{l_{a}} = \frac{e^{a + 2}}{10}$ .
Dann folgt für die Normalengleichung: $l_{a} : y = \frac{e^{a + 2}}{10} \cdot x + b$ .
Setze $W_{a} (a + 2 | 20 \cdot e^{- a - 2})$ in die Gleichung ein und löse nach $b$ auf:
$20 \cdot e^{- a - 2} = \frac{e^{a + 2}}{10} \cdot (a + 2) + b \Rightarrow b = 20 \cdot e^{- a - 2} - \frac{(a + 2) \cdot e^{a + 2}}{10}$
$b$ $=$ $20 \cdot e^{- a - 2} - \frac{(a + 2) \cdot e^{a + 2}}{10}$
$=$ $\frac{20}{e^{a + 2}} - \frac{(a + 2) \cdot e^{a + 2}}{10}$
↓
Bringe auf den Hauptnenner.
$=$ $\frac{200 - (a + 2) \cdot e^{2 a + 4}}{10 \cdot e^{a + 2}}$
Die Normalengleichung lautet also: $l_{a} : y = \frac{e^{a + 2}}{10} \cdot x + \frac{200 - (a + 2) \cdot e^{2 a + 4}}{10 \cdot e^{a + 2}}$
(Siehe mögliche Lösung.)
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne zunächst $h_{a} (a + 2) \Rightarrow y_{a}$ .
Die Gerade $l_{a}$ ist die Gerade, die im Wendepunkt $W_{a} (a + 2 | y_{a})$ senkrecht auf der Tangente $t_{a}$ steht $\Rightarrow m_{l_{a}} \cdot m_{t_{a}} = - 1 \Rightarrow m_{l_{a}} = - \frac{1}{m_{t_{a}}}$ .
Setze $W_{a} (a + 2 | y_{a})$ in die Gleichung $l_{a} : y = m_{l_{a}} \cdot x + b$ ein und löse nach $b$ auf.
$N_{a}$ ist der Schnittpunkt des Graphen von $h_{a}$ mit der $x$ -Achse.
Ermitteln Sie den Wert von $a$ , für den die Gerade $l_{a}$ durch $N_{a}$ verläuft. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Ermittle den Wert von $a$ , für den die Gerade $I_{a}$ durch $N_{a}$ verläuft
Gegeben ist $h_{a} (x) = 10 \cdot (x - a) \cdot e^{- x}$ und $l_{a} : y = \frac{e^{a + 2}}{10} \cdot x + \frac{200 - (a + 2) \cdot e^{2 a + 4}}{10 \cdot e^{a + 2}}$ .
Berechne den Schnittpunkt $N_{a}$ des Graphen von $h_{a}$ mit der $x$ -Achse $\Rightarrow h_{a} (x) = 0$ .
$0 = 10 \cdot (x - a) \cdot e^{- x}$
Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:
$x - a = 0 \Rightarrow x = a \Rightarrow N_{a} (a | 0)$
Die Gerade $l_{a}$ soll durch $N_{a}$ verlaufen.
Setze $N_{a} (a | 0)$ in $l_{a} : y = \frac{e^{a + 2}}{10} \cdot x + \frac{200 - (a + 2) \cdot e^{2 a + 4}}{10 \cdot e^{a + 2}}$ ein und löse mit CAS:
$\Rightarrow 0 = \frac{e^{a + 2}}{10} \cdot a + \frac{200 - (a + 2) \cdot e^{2 a + 4}}{10 \cdot e^{a + 2}}$
Es ist $a = \ln (\frac{10}{e^{2}}) = \ln (10) - \ln (e^{2}) = \ln (10) - 2 \approx 0,3026$ .
Der Wert von $a$ , für den die Gerade $l_{a}$ durch $N_{a}$ verläuft, ist $a = \ln (10) - 2 \approx 0,3026$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Schnittpunkt $N_{a}$ des Graphen von $h_{a}$ mit der $x$ -Achse $\Rightarrow h_{a} (x) = 0 \Rightarrow N_{a} (x_{1} | 0)$ .
Die Gerade $l_{a}$ soll durch $N_{a}$ verlaufen.
Setze $N_{a}$ in $l_{a}$ ein und löse mit CAS.

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

$b$	$=$	$20 \cdot e^{- a - 2} - \frac{(a + 2) \cdot e^{a + 2}}{10}$
	$=$	$\frac{20}{e^{a + 2}} - \frac{(a + 2) \cdot e^{a + 2}}{10}$
	↓	Bringe auf den Hauptnenner.
	$=$	$\frac{200 - (a + 2) \cdot e^{2 a + 4}}{10 \cdot e^{a + 2}}$

Aufgabe 5

Ermittle eine Gleichung für la

Hast du eine Frage oder Feedback?

Ermittle den Wert von a, für den die Gerade Ia durch Na verläuft

Hast du eine Frage oder Feedback?

Ermittle eine Gleichung für $l_{a}$

Ermittle den Wert von $a$ , für den die Gerade $I_{a}$ durch $N_{a}$ verläuft