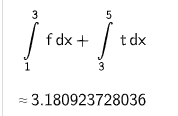B1 - lernen mit Serlo!

Aufgabe 3

Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.

Die Funktion $f$ ist gegeben durch die Gleichung $f(x)=10 \cdot(x-1) \cdot \mathrm{e}^{-x}, x \in \mathbb{R}$ .

Die 1. Ableitung ist $f'(x)=10\cdot(2-x)\cdot \mathrm{e}^{-x}$ .

Gegeben ist die Funktion $t$ mit $t(x)=-10 \cdot \mathrm{e}^{-3} \cdot x+50 \cdot \mathrm{e}^{-3}, x \in \mathbb{R}$ , und der Wendepunkt $W(3 \mid f(3))$ des Graphen von $f$ .

Weisen Sie rechnerisch nach, dass der Graph von $t$ die Tangente an den Graphen von $f$ im Punkt $W$ ist. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Weise rechnerisch nach, dass der Graph von $t$ die Tangente an den Graphen von $f$ im Punkt $W$ ist
Wenn $t$ Tangente an den Graphen von $f$ im Punkt $W$ ist, dann muss für den Punkt $W$ gelten:
$W\in t$ d.h. $f (3) = t (3)$ .
Die Steigungen der beiden Graphen müssen im Punkt $W$ gleich groß sein, d.h. $f^{'} (3) = t^{'} (3)$ .
Gegeben sind: $W(3 \mid f(3)), f(x)=10 \cdot(x-1) \cdot \mathrm{e}^{-x},t(x)=-10 \cdot \mathrm{e}^{-3} \cdot x+50 \cdot \mathrm{e}^{-3}$ ,
und nach Aufgabe 1 auch $f'(x)=10\cdot(2-x)\cdot \mathrm{e}^{-x}$ .
Überprüfung der 1. Bedingung:
Es ist $f(3)=10 \cdot(3-1) \cdot \mathrm{e}^{-3}=20\cdot \mathrm{e}^{-3}$ und $t(3)=-10 \cdot \mathrm{e}^{-3} \cdot 3+50 \cdot \mathrm{e}^{-3}=20\cdot \mathrm{e}^{-3}\;\Rightarrow\;f(3)=t(3)\;\checkmark$ .
Überprüfung der 2. Bedingung:
Für $t^{'} (x)$ erhält man: $t'(x)=-10 \cdot \mathrm{e}^{-3}$
Dann ist $f'(3)=10\cdot(2-3)\cdot \mathrm{e}^{-3}=-10 \cdot \mathrm{e}^{-3}=t'(3)\;\checkmark$ .
Die beiden Bedingungen sind erfüllt und der Graph von $t$ ist die Tangente an den Graphen von $f$ im Punkt $W(3 \mid f(3))$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Wenn $t$ Tangente an den Graphen von $f$ im Punkt $W$ ist, dann muss für den Punkt $W$ gelten:
$W\in t$ , d.h. $f (3) = t (3)$ .
Die Steigungen der beiden Graphen müssen im Punkt $W$ gleich groß sein, d.h. $f^{'} (3) = t^{'} (3)$ .
Überprüfe die beiden Bedingungen.
Die Schnittpunkte der in Aufgabe 3 gegebenen Tangente mit den beiden Koordinatenachsen legen zusammen mit dem Koordinatenursprung $O(0 \mid 0)$ ein Dreieck fest.
Berechnen Sie den Umfang dieses Dreiecks. (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
Berechne den Umfang dieses Dreiecks
Skizze des Dreiecks.
Es ist $t(x)=-10 \cdot \mathrm{e}^{-3} \cdot x+50 \cdot \mathrm{e}^{-3}$ .
Der Schnittpunkt der Tangente mit der y-Achse ist $t(0)\;\Rightarrow\;t(0)=50 \cdot \mathrm{e}^{-3}\approx2{,}4894$ .
Dann ist $S_y(0|50 \cdot \mathrm{e}^{-3})$ , gerundet $S_y(0|2{,}4894)$ .
Für den Schnittpunkt der Tangente mit der x-Achse setze $t (x) = 0$ .
$0=-10 \cdot \mathrm{e}^{-3} \cdot x+50 \cdot \mathrm{e}^{-3}=10\cdot\mathrm{e}^{-3}(-x+5)\;\Rightarrow\;x=5$
Dann ist $S_{x} (5 ∣ 0)$ .
Für den Abstand von $2$ Punkten verwende $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ .
Setze die Koordinaten von $S_{x}$ und $S_{y}$ ein:
$d=\sqrt{(5-0)^2+(0-50 \cdot \mathrm{e}^{-3})^2}=\sqrt{25+2500\cdot\mathrm{e}^{-6}}\approx5{,}5854$
Die Länge dieser Strecke beträgt rund $5{,}5854 \;\mathrm{LE}$ .
Der Umfang des Dreiecks ist die Summe der drei Seiten des Dreiecks.
$U=\overline {OS_x}+\overline {OS_y}+ d=5+2{,}4894+5{,}5854\approx 13{,}075$
Der Umfang dieses Dreiecks beträgt rund $13{,}075\;\mathrm{LE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Schnittpunkt der Tangente mit der y-Achse $\;\Rightarrow\;S_y(x_1|y_1)$ .
Berechne den Schnittpunkt der Tangente mit der x-Achse $\;\Rightarrow\;S_x(x_2|y_2)$ .
Für den Abstand von $2$ Punkten verwende $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ .
Der Umfang des Dreiecks ist die Summe der drei Seiten des Dreiecks $U = y_{1} + y_{2} + d$ .
Im Intervall $[1; 5]$ begrenzen der Graph von $f$ und die in Aufgabe 3 gegebene Tangente zusammen mit der $x$ -Achse eine Fläche $F$ (siehe Abbildung 2).
Bestimmen Sie den Flächeninhalt von $F$ auf vier Nachkommastellen gerundet. (3 P)
Abbildung 2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Bestimme den Flächeninhalt von $F$ auf vier Nachkommastellen gerundet
Bekannt ist: Im Intervall $[1; 5]$ begrenzen der Graph von $f$ und die in Aufgabe 2 gegebene Tangente zusammen mit der $x$ -Achse eine Fläche $F$ und es ist $W(3 \mid f(3))$ .
Die Fläche $F$ besteht aus 2 Teilen $F = A_{1} + A_{2}$ .
Die Grenzen für die Flächenberechnung der ersten Fläche sind die linke Intervallgrenze $1$ und die x-Koordinate des Wendepunkte $x = 3$ .
Die Grenzen für die Flächenberechnung der zweiten Fläche sind die x-Koordinate des Wendepunkte $x = 3$ und die rechte Intervallgrenze $5$ .
Dann gilt: $A_1=\displaystyle\int_1^3f(x)\;\mathrm{d}x$ und $A_2=\displaystyle\int_3^5t(x)\;\mathrm{d}x$ .
Der CAS-Rechner liefert das Ergebnis für $F = A_{1} + A_{2}$ :
Der Flächeninhalt von $F$ beträgt auf vier Nachkommastellen gerundet $3{,}1809\;\mathrm{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Fläche $F$ besteht aus 2 Teilen $F = A_{1} + A_{2}$ .
Die Grenzen für die Flächenberechnung der ersten Fläche sind die linke Intervallgrenze $1$ und die x-Koordinate des Wendepunkte $x = 3$ .
Die Grenzen für die Flächenberechnung der zweiten Fläche sind die x-Koordinate des Wendepunkte $x = 3$ und die rechte Intervallgrenze $5$ .
Berechne mit dem CAS die Summe der beiden Integrale.
Runde auf vier Nachkommastellen.

Aufgabe 3

Weise rechnerisch nach, dass der Graph von ttt die Tangente an den Graphen von fff im Punkt WWW ist

Hast du eine Frage oder Feedback?

Berechne den Umfang dieses Dreiecks

Hast du eine Frage oder Feedback?

Bestimme den Flächeninhalt von FFF auf vier Nachkommastellen gerundet

Hast du eine Frage oder Feedback?

Weise rechnerisch nach, dass der Graph von $t$ die Tangente an den Graphen von $f$ im Punkt $W$ ist

Bestimme den Flächeninhalt von $F$ auf vier Nachkommastellen gerundet