B2 - lernen mit Serlo!

Aufgabe 1

Die Abbildung zeigt den Graphen der in $ℝ$ definierten Funktion $f$ mit $f (x) = - \frac{5}{16} x^{4} + 5 x^{3}$ .

Zeigen Sie rechnerisch, dass der Punkt $(12 | 2160)$ ein Hochpunkt des Graphen von $f$ ist und dass die Tangente an den Graphen von $f$ im Punkt $(0 | 0)$ parallel zur $x$ -Achse verläuft. (5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Zeige rechnerisch, dass der Punkt $(12 | 2160)$ ein Hochpunkt des Graphen von $f$ ist
Gegeben ist $f (x) = - \frac{5}{16} x^{4} + 5 x^{3}$ .
Berechne $f^{'} (x)$ und $f^{''} (x)$ :
$f^{'} (x) = - \frac{5}{4} x^{3} + 15 x^{2}$
$f^{''} (x) = - \frac{15}{4} x^{2} + 30 x$
Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
$\Rightarrow 0 = - \frac{5}{4} x^{3} + 15 x^{2} = 5 x^{2} \cdot (- \frac{1}{4} x + 3)$
Mit dem Satz vom Nullprodukt folgt:
$x = 0 \lor - \frac{1}{4} x + 3 = 0 \Rightarrow x = 12$
Lokale Extremstellen sind $x = 0$ oder $x = 12$ .
Nach Aufgabenstellung muss nur $x = 12$ beachtet werden.
Die hinreichende Bedingung für ein Extremum ist $f^{''} (x) \neq 0$ .
$\Rightarrow f^{''} (12) = - \frac{15}{4} \cdot 12^{2} + 30 \cdot 12 = - 180 < 0 \Rightarrow$ Maximum
Berechne $f (12) = - \frac{5}{16} \cdot 12^{4} + 5 \cdot 12^{3} = 2160$ .
Der Punkt $(12 | 2160)$ ist also ein Hochpunkt des Graphen von $f$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne $f^{'} (x)$ und $f^{''} (x)$ .
Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ $\Rightarrow x_{1}$ und $x_{2}$ .
Die hinreichende Bedingung für ein Extremum ist $f^{''} (x) \neq 0$ .
Nach Aufgabenstellung muss nur $x = 12$ untersucht werden.
Teil 2
Es ist $f^{'} (0) = 0$ und $f (0) = 0$ . Was folgt daraus?
Bestimmen Sie eine Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft.
Zeichnen Sie in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat. (6 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Bestimme eine Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft
Berechne die Wendepunkte:
Die notwendige Bedingung für einen Wendepunkt ist $f^{''} (x) = 0$ .
$\Rightarrow 0 = - \frac{15}{4} x^{2} + 30 x = 15 \cdot x (- \frac{1}{4} \cdot x + 2)$
Mit dem Satz vom Nullprodukt folgt:
$x = 0 \lor - \frac{1}{4} x + 2 = 0 \Rightarrow x = 8$
Wendestellen liegen bei $x = 0$ oder $x = 8$ vor, wenn die hinreichende Bedingung $f^{'''} (x) \neq 0$ erfüllt ist.
Berechne $f^{'''} (x) = - \frac{15}{2} x + 30 \Rightarrow f^{''} (0) = 30 \neq 0$ und $f^{'''} (8) = - \frac{15}{2} \cdot 8 + 30 = - 30 \neq 0$
Die Bedingung ist erfüllt, d.h. Wendestellen liegen bei $x = 0$ oder $x = 8$ vor.
Berechne $f (0) = 0$ und $f (8) = - \frac{5}{16} \cdot 8^{4} + 5 \cdot 8^{3} = 1280$ .
Die Wendepunkte haben die Koordinaten $W P_{1} (0 | 0)$ und $W P_{2} (8 | 1280)$ .
Für die Geradengleichung $g$ benutze die Zwei-Punkte-Form der Geradengleichung:
$y = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot (x - x_{1}) + y_{1} \Rightarrow y = \frac{1280 - 0}{8 - 0} \cdot (x - 0) + 0$
$\Rightarrow g : y = 160 \cdot x$
Die Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft, lautet $y = 160 \cdot x$ .
Zeichne in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat
Die zu $g$ parallele Gerade hat für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Die notwendige Bedingung für einen Wendepunkt ist $f^{''} (x) = 0$ $\Rightarrow x_{1}$ und $x_{2}$ .
Die hinreichende Bedingung ist $f^{'''} (x) \neq 0$ .
Berechne $f (x_{1})$ und $f (x_{2})$ $\Rightarrow W P_{1} (x_{1} | f (x_{1}))$ und $W P_{2} (x_{2} | f (x_{2}))$ .
Für die Geradengleichung $g$ benutze die Zwei-Punkte-Form der Geradengleichung: $y = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \cdot (x - x_{1}) + y_{1}$
Teil 2
Zeichne die zu $g$ parallele Gerade, die für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat, in die Abbildung ein.
Die Punkte $O (0 | 0), B (b | 0)$ und $C (b | f (b))$ bilden für jede reelle Zahl $b$ mit $0 < b < 16$ ein Dreieck $O B C$ .
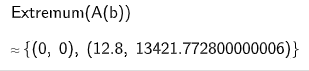
Ermitteln Sie denjenigen Wert von $b$ , für den der Flächeninhalt des Dreiecks $O B C$ maximal wird, und geben Sie diesen Flächeninhalt an.
$[$ Hinweis: Eine Betrachtung der Randwerte ist nicht erforderlich. $]$ (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Ermittle denjenigen Wert von $b$ , für den der Flächeninhalt des Dreiecks $O B C$ maximal wird, und gib diesen Flächeninhalt an
Abbildung mit einem eingezeichneten Dreieck $O B C$ :
Abbildung mit Dreieck
Für den Flächeninhalt des Dreiecks gilt: $A = \frac{1}{2} \cdot g \cdot h$
$\Rightarrow A (b) = \frac{1}{2} \cdot b \cdot f (b) = \frac{1}{2} \cdot b \cdot (- \frac{5}{16} \cdot b^{4} + 5 \cdot b^{3}) = - \frac{5}{32} \cdot b^{5} + \frac{5}{2} \cdot b^{4}$
Bestimme das absolute Maximum von $A (b)$ mit dem CAS-Rechner im Intervall $[0; 16]$ .
Das Maximum hat die gerundeten Koordinaten $(12,8 | 13421,77)$ .
Für $b = 12,8$ hat das Dreieck $O B C$ den maximalen Flächeninhalt von rund $13421,77 FE$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für den Flächeninhalt des Dreiecks gilt: $A = \frac{1}{2} \cdot g \cdot h \Rightarrow A (b) = \frac{1}{2} \cdot b \cdot f (b)$ .
Bestimme das absolute Maximum von $A (b)$ mit dem CAS-Rechner im Intervall $[0; 16]$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 1

Zeige rechnerisch, dass der Punkt (12|2160) ein Hochpunkt des Graphen von f ist

Hast du eine Frage oder Feedback?

Bestimme eine Gleichung der Geraden g, die durch die beiden Wendepunkte des Graphen von f verläuft

Zeichne in die Abbildung eine Gerade ein, die parallel zu g ist und für 0≤x≤8 mit dem Graphen von f genau einen Punkt gemeinsam hat

Hast du eine Frage oder Feedback?

Ermittle denjenigen Wert von b, für den der Flächeninhalt des Dreiecks OBC maximal wird, und gib diesen Flächeninhalt an

Hast du eine Frage oder Feedback?

Zeige rechnerisch, dass der Punkt $(12 | 2160)$ ein Hochpunkt des Graphen von $f$ ist

Bestimme eine Gleichung der Geraden $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft

Zeichne in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0 \leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat

Ermittle denjenigen Wert von $b$ , für den der Flächeninhalt des Dreiecks $O B C$ maximal wird, und gib diesen Flächeninhalt an