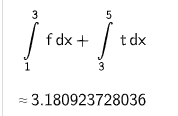Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Die Funktion ist gegeben durch die Gleichung .
Die 1. Ableitung ist .
Gegeben ist die Funktion mit , und der Wendepunkt des Graphen von .
Weisen Sie rechnerisch nach, dass der Graph von die Tangente an den Graphen von im Punkt ist. (4 P)
Die Schnittpunkte der in Aufgabe 2 gegebenen Tangente mit den beiden Koordinatenachsen legen eine Strecke fest.
Berechnen Sie die Länge dieser Strecke. (3 P)
Im Intervall begrenzen der Graph von und die in Aufgabe 2 gegebene Tangente zusammen mit der -Achse eine Fläche (siehe Abbildung 2).
Bestimmen Sie den Flächeninhalt von . (3 P)
Abbildung 2