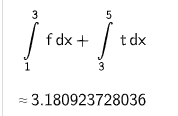B1

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = 10 \cdot (x - 1) \cdot e^{- x}, x \in ℝ$ .
Der Graph von $f$ ist in Abbildung 1 dargestellt.
Abbildung 1
1. Begründen Sie, dass $x = 1$ die einzige Nullstelle von $f$ ist. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
  Begründe, dass $x = 1$ die einzige Nullstelle von $f$ ist
  Gegeben ist $f (x) = 10 \cdot (x - 1) \cdot e^{- x}$ .
  Für die Nullstellen löse die Gleichung $f (x) = 0$ .
  $0 = 10 \cdot (x - 1) \cdot e^{- x}$
  Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:
  $\Rightarrow x - 1 = 0 \Rightarrow x = 1$
  Demnach ist $x = 1$ die einzige Nullstelle.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Gleichung $f (x) = 0$ .
2. Zeigen Sie: $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Produktregel, Quotientenregel und Kettenregel
  Zeige: $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$
  Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung:
  $f^{'} (x) = 10 \cdot (1 \cdot e^{- x} + (x - 1) \cdot e^{- x} \cdot (- 1)) = 10 \cdot (2 - x) \cdot e^{- x}$
  Die erste Ableitung ist $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung.
3. Untersuchen Sie $f$ rechnerisch auf lokale Extremstellen. $[$ (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Untersuche $f$ rechnerisch auf lokale Extremstellen
  Die erste Ableitung ist $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$ .
  Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
  $f^{'} (x) = 0 \Rightarrow 0 = 10 \cdot (2 - x) \cdot e^{- x}$
  Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:
  $2 - x = 0 \Rightarrow x = 2$
  Die hinreichende Bedingung für ein Extremum ist $f^{''} (x) \neq 0$ .
  Bilde mithilfe der Produkt- und Kettenregel die 2. Ableitung:
  $f^{''} (x) = 10 \cdot ((- 1) \cdot e^{- x} + (2 - x) \cdot e^{- x} \cdot (- 1)) = 10 \cdot (x - 3) \cdot e^{- x}$
  $f^{''} (2) = 10 \cdot (2 - 3) \cdot e^{- 2} = - 10 \cdot e^{- 2} < 0$
  Die Funktion $f$ hat genau eine lokale Extremstelle.
  Der Graph von $f$ hat bei $x = 2$ ein lokales Maximum.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
  Bilde die 1. Ableitung und löse die Gleichung $f^{'} (x) = 0 \Rightarrow x_{1}$ .
  Die hinreichende Bedingung für ein Extremum ist $f^{''} (x) \neq 0$ .
  Bilde die 2. Ableitung und überprüfe $f^{''} (x_{1})$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = 10 \cdot (x - 1) \cdot e^{- x}, x \in ℝ$ .
Die 1. Ableitung ist $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$ .
Gegeben ist die Funktion $t$ mit $t (x) = - 10 \cdot e^{- 3} \cdot x + 50 \cdot e^{- 3}, x \in ℝ$ , und der Wendepunkt $W (3 | f (3))$ des Graphen von $f$ .
1. Weisen Sie rechnerisch nach, dass der Graph von $t$ die Tangente an den Graphen von $f$ im Punkt $W$ ist. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Weise rechnerisch nach, dass der Graph von $t$ die Tangente an den Graphen von $f$ im Punkt $W$ ist
  Wenn $t$ Tangente an den Graphen von $f$ im Punkt $W$ ist, dann muss für den Punkt $W$ gelten:
  $W \in t$ d.h. $f (3) = t (3)$ .
  Die Steigungen der beiden Graphen müssen im Punkt $W$ gleich groß sein, d.h. $f^{'} (3) = t^{'} (3)$ .
  Gegeben sind: $W (3 | f (3)), f (x) = 10 \cdot (x - 1) \cdot e^{- x}, t (x) = - 10 \cdot e^{- 3} \cdot x + 50 \cdot e^{- 3}$ ,
  und nach Aufgabe 1 auch $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$ .
  Überprüfung der 1. Bedingung:
  Es ist $f (3) = 10 \cdot (3 - 1) \cdot e^{- 3} = 20 \cdot e^{- 3}$ und $t (3) = - 10 \cdot e^{- 3} \cdot 3 + 50 \cdot e^{- 3} = 20 \cdot e^{- 3} \Rightarrow f (3) = t (3) ✓$ .
  Überprüfung der 2. Bedingung:
  Für $t^{'} (x)$ erhält man: $t^{'} (x) = - 10 \cdot e^{- 3}$
  Dann ist $f^{'} (3) = 10 \cdot (2 - 3) \cdot e^{- 3} = - 10 \cdot e^{- 3} = t^{'} (3) ✓$ .
  Die beiden Bedingungen sind erfüllt und der Graph von $t$ ist die Tangente an den Graphen von $f$ im Punkt $W (3 | f (3))$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wenn $t$ Tangente an den Graphen von $f$ im Punkt $W$ ist, dann muss für den Punkt $W$ gelten:
  $W \in t$ , d.h. $f (3) = t (3)$ .
  Die Steigungen der beiden Graphen müssen im Punkt $W$ gleich groß sein, d.h. $f^{'} (3) = t^{'} (3)$ .
  Überprüfe die beiden Bedingungen.
2. Die Schnittpunkte der in Aufgabe 2 gegebenen Tangente mit den beiden Koordinatenachsen legen eine Strecke fest.
  Berechnen Sie die Länge dieser Strecke. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
  Berechne die Länge dieser Strecke
  Es ist $t (x) = - 10 \cdot e^{- 3} \cdot x + 50 \cdot e^{- 3}$ .
  Der Schnittpunkt der Tangente mit der y-Achse ist $t (0) \Rightarrow t (0) = 50 \cdot e^{- 3}$ .
  Dann ist $S_{y} (0 | 50 \cdot e^{- 3})$ .
  Für den Schnittpunkt der Tangente mit der x-Achse setze $t (x) = 0$ .
  $0 = - 10 \cdot e^{- 3} \cdot x + 50 \cdot e^{- 3} = 10 \cdot e^{- 3} (- x + 5) \Rightarrow x = 5$
  Dann ist $S_{x} (5 | 0)$ .
  Für den Abstand von $2$ Punkten verwende $d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$ .
  Setze die Koordinaten von $S_{x}$ und $S_{y}$ ein:
  $d = \sqrt{(5 - 0)^{2} + (0 - 50 \cdot e^{- 3})^{2}} = \sqrt{25 + 2500 \cdot e^{- 6}} \approx 5,5854$
  Die Länge dieser Strecke beträgt rund $5,5854 LE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Schnittpunkt der Tangente mit der y-Achse $\Rightarrow S_{y} (x_{1} | y_{1})$ .
  Berechne den Schnittpunkt der Tangente mit der x-Achse $\Rightarrow S_{x} (x_{2} | y_{2})$ .
  Für den Abstand von $2$ Punkten verwende $d = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$ .
3. Im Intervall $[1; 5]$ begrenzen der Graph von $f$ und die in Aufgabe 2 gegebene Tangente zusammen mit der $x$ -Achse eine Fläche $F$ (siehe Abbildung 2).
  Bestimmen Sie den Flächeninhalt von $F$ . (3 P)
  Abbildung 2
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Bestimme den Flächeninhalt von $F$
  Bekannt ist: Im Intervall $[1; 5]$ begrenzen der Graph von $f$ und die in Aufgabe 2 gegebene Tangente zusammen mit der $x$ -Achse eine Fläche $F$ und es ist $W (3 | f (3))$ .
  Die Fläche $F$ besteht aus 2 Teilen $F = A_{1} + A_{2}$ .
  Die Grenzen für die Flächenberechnung der ersten Fläche sind die linke Intervallgrenze $1$ und die x-Koordinate des Wendepunkte $x = 3$ .
  Die Grenzen für die Flächenberechnung der zweiten Fläche sind die x-Koordinate des Wendepunkte $x = 3$ und die rechte Intervallgrenze $5$ .
  Dann gilt: $A_{1} = \int_{1}^{3} f (x) d x$ und $A_{2} = \int_{3}^{5} t (x) d x$ .
  Der CAS-Rechner liefert das Ergebnis für $F = A_{1} + A_{2}$ :
  Der Flächeninhalt von $F$ beträgt auf vier Nachkommastellen gerundet $3,18 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Fläche $F$ besteht aus 2 Teilen $F = A_{1} + A_{2}$ .
  Die Grenzen für die Flächenberechnung der ersten Fläche sind die linke Intervallgrenze $1$ und die x-Koordinate des Wendepunkte $x = 3$ .
  Die Grenzen für die Flächenberechnung der zweiten Fläche sind die x-Koordinate des Wendepunkte $x = 3$ und die rechte Intervallgrenze $5$ .
  Berechne mit dem CAS die Summe der beiden Integrale.
  Runde auf vier Nachkommastellen.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = 10 \cdot (x - 1) \cdot e^{- x}, x \in ℝ$ .
Die Gerade $g$ ist die Parallele zur $x$ -Achse durch den Hochpunkt $H (2 | f (2))$ des Graphen von $f$ . Die $y$ -Achse, $g$ und der Graph von $f$ schließen eine Fläche ein (orange gefärbte Fläche in Abbildung 3).
Abbildung 3
1. Ermitteln Sie den Inhalt dieser Fläche. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Ermittle den Inhalt dieser Fläche
  Ermittele zunächst die Gleichung der Geraden $g$ :
  Die Gerade $g$ verläuft durch den Hochpunkt $H P (2 | f (2))$ .
  Berechne $f (2) = 10 \cdot (2 - 1) \cdot e^{- 2} = 10 \cdot e^{- 2} \Rightarrow H P (2 | 10 \cdot e^{- 2})$ .
  Die Gerade $g$ hat die Steigung $m = 0 \Rightarrow g : y = 10 \cdot e^{- 2}$ .
  Für den Flächeninhalt erhält man dann: $\int_{0}^{2} (g - f (x)) d x$
  Die Berechnung mit CAS liefert das folgende Ergebnis:
  Der Inhalt dieser Fläche beträgt rund $5,4134 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ermittele die Gleichung der Geraden $g$ , die durch den Hochpunkt $H P (2 | f (2))$ verläuft.
  Für den Flächeninhalt erhält man dann: $\int_{0}^{2} (g - f (x)) d x$
2. $Q_{u} (u | f (u)), 0 < u < 2$ , ist ein Punkt auf dem Graphen von $f$ . Die Parallelen durch $Q_{u}$ zu den beiden Koordinatenachsen werden mit $p_{x}$ und $p_{y}$ bezeichnet. Die $y$ -Achse, $g, p_{x}$ und $p_{y}$ begrenzen ein Rechteck (siehe schraffierte Fläche in Abbildung 3).
  Ermitteln Sie den Flächeninhalt dieses Rechtecks für den Fall, dass $Q_{u}$ mit dem Schnittpunkt übereinstimmt, den der Graph von $f$ mit der $x$ -Achse hat. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
  Ermittle den Flächeninhalt dieses Rechtecks für den Fall, dass $Q_{u}$ mit dem Schnittpunkt übereinstimmt, den der Graph von $f$ mit der $x$ -Achse hat
  Nach Aufgabe 1) hat der Graph von $f$ nur eine Nullstelle bei $x = 1$ . Der Punkt $Q_{1}$ hat die Koordinaten $Q_{1} (1 | 0)$ .
  Den Flächeninhalt eines Rechtecks berechnet man mit $A = a \cdot b$ .
  Dabei ist $a = 1$ und $b = 10 \cdot e^{- 2}$ (Abstand der Geraden $g$ von der x-Achse).
  $\Rightarrow A = 1 \cdot 10 \cdot e^{- 2} = 10 \cdot e^{- 2} \approx 1,3534$
  Der Flächeninhalt dieses Rechtecks beträgt rund $1,3534 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Nach Aufgabe 1) hat der Graph von $f$ nur eine Nullstelle bei $x = 1$ . Der Punkt $Q_{1}$ hat die Koordinaten $Q_{1} (1 | 0)$ .
  Den Flächeninhalt eines Rechtecks berechnet man mit $A = a \cdot b$ .
  Setze $a$ und $b$ ein.
3. Untersuchen Sie, um wie viel Prozent sich der Wert aus b) maximal vergrößern lässt, wenn für $Q_{u} (u | f (u))$ eine andere Position mit $0 < u < 2$ gewählt wird. (5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
  Untersuche, um wie viel Prozent sich der Wert aus b) maximal vergrößern lässt, wenn für $Q_{u} (u | f (u))$ eine andere Position mit $0 < u < 2$ gewählt wird
  Es sind $Q_{u} (u | f (u))$ und $g : y = 10 \cdot e^{- 2}$ .
  Funktionsgleichung für $A (u)$ ermitteln
  Die eine Rechteckseite hat die Länge $u$ und die andere Rechteckseite hat die Länge $g - f (u) = 10 \cdot e^{- 2} - 10 \cdot (u - 1) \cdot e^{- u}$
  $\Rightarrow A (u) = u \cdot (10 \cdot e^{- 2} - 10 \cdot (u - 1) \cdot e^{- u})$
  Bestimmung des maximalen Flächeninhalts
  Lasse Dir den Graphen von $A (u)$ anzeigen und bestimme das Maximum.
  Für $u \approx 0,4850$ wird $A (u)$ maximal.
  Dabei ist $A_{max} \approx 2,1942 FE$ .
  Berechnung der prozentualen Vergrößerung
  Für die prozentuale Vergrößerung erhält man mit $A \approx 1,3534$ :
  $\frac{A_{max}}{A} = \frac{2,1942}{1,3534} \approx 1,621$
  Der Wert aus b) lässt sich maximal um etwa $62 %$ vergrößern.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es sind $Q_{u} (u | f (u))$ und $g : y = 10 \cdot e^{- 2}$ .
  Die eine Rechteckseite hat die Länge $u$ und die andere Rechteckseite hat die Länge $g - f (u) \Rightarrow$ berechne $A (u)$ .
  Lasse Dir den Graphen von $A (u)$ anzeigen, bestimme das Maximum $A_{max}$ .
  Für die prozentuale Vergrößerung erhält man mit $A$ aus Aufgabe b): $\frac{A_{max}}{A}$ .
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Die Gerade mit der Gleichung $y = x$ wird als "1. Winkelhalbierende" bezeichnet. Es gibt genau eine Tangente $t_{R}$ an den Graphen von $f$ , die parallel zur 1. Winkelhalbierenden ist. Eine mit vier Nachkommastellen angegebene näherungsweise Gleichung für $t_{R}$ ist $y = x - 0,3824$ .
Ermitteln Sie rechnerisch den Abstand, den die Tangente $t_{R}$ von der 1. Winkelhalbierenden hat.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Punkte berechnen
Ermittle rechnerisch den Abstand, den die Tangente $t_{R}$ von der 1. Winkelhalbierenden hat
Gegeben ist $t_{R} : y = x - 0,3824$ .
Der Abstand zweier Geraden ist immer die kürzeste Entfernung zwischen diesen Geraden.
Betrachtet man die "2. Winkelhalbierende" $y = - x$ , so steht diese senkrecht auf der "1. Winkelhalbierenden" und schneidet die Tangente $t_{R}$ im Punkt $S$ .
Der gesuchte Abstand $d$ ist dann die Entfernung des Punktes S vom Koordinatenursprung.
Berechne den Schnittpunkt zwischen der "2. Winkelhalbierenden" $y = - x$ und $t_{R}$ :
$x - 0,3824 = - x \Rightarrow 2 x = 0,3824 \Rightarrow x_{S} = 0,1912$ und $y_{S} = - 0,1912$ .
Der Schnittpunkt hat die Koordinaten $S (0,1912 | - 0,1912)$ .
Dann gilt für $d (O; S) = \sqrt{{0,1912}^{2} + {0,1912}^{2}} \approx 0,27$ .
Der Abstand, den die Tangente $t_{R}$ von der 1. Winkelhalbierenden hat, beträgt rund $0,27 L E$ .
Die folgende Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur zur Veranschaulichung.
Betrachtet man die "2. Winkelhalbierende" $y = - x$ , so steht diese senkrecht auf der "1. Winkelhalbierenden" und schneidet die Tangente $t_{R}$ im Punkt $S$ .
Der gesuchte Abstand $d$ ist dann die Entfernung des Punktes S vom Koordinatenursprung.
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 5
Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = 10 \cdot (x - 1) \cdot e^{- x}, x \in ℝ$ .
Die Funktion $f$ gehört zur Schar $h_{a}$ , die gegeben ist durch
$h_{a} (x) = 10 \cdot (x - a) \cdot e^{- x}, x \in ℝ, a \in ℝ$ .
Ohne Nachweis kann verwendet werden $h_{a}^{''} (x) = 10 \cdot (x - a - 2) \cdot e^{- x}$ . Der Graph von $h_{a}$ besitzt genau einen Wendepunkt $W_{a}$ .
1. Ermitteln Sie die Koordinaten des Wendepunktes $W_{a}$ .
  $[$ Hinweis: Ein Nachweis der hinreichenden Bedingung ist hier nicht erforderlich. $]$
  (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Ermittle die Koordinaten des Wendepunktes $W_{a}$ .
  Gegeben ist $h_{a} (x) = 10 \cdot (x - a) \cdot e^{- x}$ und $h_{a}^{''} (x) = 10 \cdot (x - a - 2) \cdot e^{- x}$ .
  Die notwendige Bedingung für eine Wendestelle ist $h_{a}^{''} (x) = 0$ .
  $h_{a}^{''} (x) = 0 \Rightarrow 0 = 10 \cdot (x - a - 2) \cdot e^{- x}$
  Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:
  $x - a - 2 = 0 \Rightarrow x = a + 2$
  Ein Nachweis der hinreichenden Bedingung ist hier nicht erforderlich, d.h. man erhält genau eine Wendestelle an der Stelle $x = a + 2$ .
  Die y-Koordinate des Wendepunktes ist dann:
  $h_{a} (a + 2) = 10 \cdot (a + 2 - a) \cdot e^{- a - 2} = 20 \cdot e^{- a - 2}$
  Bekannt ist: Der Graph von $h_{a}$ besitzt genau einen Wendepunkt $W_{a}$ .
  $\Rightarrow W_{a} (a + 2 | 20 \cdot e^{- a - 2})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die notwendige Bedingung für eine Wendestelle ist $h_{a}^{''} (x) = 0$ .
  Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung und die 2. Ableitung.
  Löse die Gleichung $h_{a}^{''} (x) = 0$ .
2. $t_{a}$ ist die Tangente im Wendepunkt $W_{a}$ . Eine Gleichung für $t_{a}$ ist $y = - 10 \cdot e^{- a - 2} \cdot x + 10 (a + 4) \cdot e^{- a - 2}$ .
  Für $a \neq - 4$ begrenzt $t_{a}$ mit den beiden Koordinatenachsen ein Dreieck. Leiten Sie einen Term für den Flächeninhalt $A_{D}$ des Dreiecks her. (4 P)
  $[$ Mögliche Lösung: $A_{D} (a) = 5 \cdot (a + 4)^{2} \cdot e^{- a - 2}$ $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
  Leite einen Term für den Flächeninhalt $A_{D}$ des Dreiecks her
  Bestimme die Schnittpunkte von $t_{a}$ mit den Koordinatenachsen:
  Schnitt mit der y-Achse: $x = 0 \Rightarrow y = - 10 \cdot e^{- a - 2} \cdot 0 + 10 (a + 4) \cdot e^{- a - 2} = 10 (a + 4) \cdot e^{- a - 2}$
  $\Rightarrow S_{y} (0 | 10 (a + 4) \cdot e^{- a - 2})$
  Schnitt mit der x-Achse:
  $y = 0 \Rightarrow 0 = - 10 \cdot e^{- a - 2} \cdot x + 10 (a + 4) \cdot e^{- a - 2}$
  $\Rightarrow x = \frac{10 (a + 4) \cdot e^{- a - 2}}{10 \cdot e^{- a - 2}} = a + 4$
  $\Rightarrow S_{x} (a + 4 | 0)$
  Für den Flächeninhalt des Dreiecks erhält man dann:
  $A_{D} = \frac{1}{2} \cdot x \cdot y = \frac{1}{2} \cdot (a + 4) \cdot (10 \cdot (a + 4) \cdot e^{- a - 2})$
  $A_{D} = 5 \cdot (a + 4)^{2} \cdot e^{- a - 2}$
  Der Term für den Flächeninhalt $A_{D}$ des Dreiecks lautet $A_{D} = 5 \cdot (a + 4)^{2} \cdot e^{- a - 2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Schnittpunkte von $t_{a}$ mit den Koordinatenachsen $\Rightarrow x_{1}$ und $y_{1}$ .
  Für den Flächeninhalt des Dreiecks erhält man dann $A_{D} = \frac{1}{2} \cdot x_{1} \cdot y_{1}$ .
3. Ermitteln Sie einen Wert von $a$ , für den die Dreiecksfläche die Größe $10 FE$ hat. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
  Ermittle einen Wert von $a$ , für den die Dreiecksfläche die Größe $10 FE$ hat
  Es ist $A_{D} = 5 \cdot (a + 4)^{2} \cdot e^{- a - 2}$ .
  Löse die Gleichung $10 = 5 \cdot (a + 4)^{2} \cdot e^{- a - 2} \Rightarrow 2 = (a + 4)^{2} \cdot e^{- a - 2}$ .
  $NLöse (2 = (a + 4)^{2} \cdot e^{- a - 2}, a)$ mit dem Ergebnis:
  $a \approx - 4,4214 \lor a \approx - 3,2388 \lor a \approx 0,1559$
  Man erhält drei Werte für $a$ , sodass die Dreiecksfläche den Flächeninhalt $10 FE$ hat.
  Alternativ können die Funktionen $A_{D}$ und $y = 10$ gezeichnet werden und man bestimmt grafisch die Schnittpunkte zwischen ihnen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Aus Aufgabe c) $\Rightarrow A_{D}$ .
  Löse die Gleichung $A_{D} = 10$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B1

Aufgabe 1

Begründe, dass x=1 die einzige Nullstelle von f ist

Hast du eine Frage oder Feedback?

Zeige: f′(x)=10⋅(2−x)⋅e−x

Hast du eine Frage oder Feedback?

Untersuche f rechnerisch auf lokale Extremstellen

Hast du eine Frage oder Feedback?

Aufgabe 2

Weise rechnerisch nach, dass der Graph von t die Tangente an den Graphen von f im Punkt W ist

Hast du eine Frage oder Feedback?

Berechne die Länge dieser Strecke

Hast du eine Frage oder Feedback?

Bestimme den Flächeninhalt von F

Hast du eine Frage oder Feedback?

Aufgabe 3

Ermittle den Inhalt dieser Fläche

Hast du eine Frage oder Feedback?

Ermittle den Flächeninhalt dieses Rechtecks für den Fall, dass Qu mit dem Schnittpunkt übereinstimmt, den der Graph von f mit der x-Achse hat

Hast du eine Frage oder Feedback?

Untersuche, um wie viel Prozent sich der Wert aus b) maximal vergrößern lässt, wenn für Qu(u|f(u)) eine andere Position mit 0<u<2 gewählt wird

Hast du eine Frage oder Feedback?

Aufgabe 4

Ermittle rechnerisch den Abstand, den die Tangente tR von der 1. Winkelhalbierenden hat

Aufgabe 5

Ermittle die Koordinaten des Wendepunktes Wa.

Hast du eine Frage oder Feedback?

Leite einen Term für den Flächeninhalt AD des Dreiecks her

Hast du eine Frage oder Feedback?

Ermittle einen Wert von a, für den die Dreiecksfläche die Größe 10FE hat

Hast du eine Frage oder Feedback?

Begründe, dass $x = 1$ die einzige Nullstelle von $f$ ist

Zeige: $f^{'} (x) = 10 \cdot (2 - x) \cdot e^{- x}$

Untersuche $f$ rechnerisch auf lokale Extremstellen

Weise rechnerisch nach, dass der Graph von $t$ die Tangente an den Graphen von $f$ im Punkt $W$ ist

Bestimme den Flächeninhalt von $F$

Ermittle den Flächeninhalt dieses Rechtecks für den Fall, dass $Q_{u}$ mit dem Schnittpunkt übereinstimmt, den der Graph von $f$ mit der $x$ -Achse hat

Untersuche, um wie viel Prozent sich der Wert aus b) maximal vergrößern lässt, wenn für $Q_{u} (u | f (u))$ eine andere Position mit $0 < u < 2$ gewählt wird

Ermittle rechnerisch den Abstand, den die Tangente $t_{R}$ von der 1. Winkelhalbierenden hat

Ermittle die Koordinaten des Wendepunktes $W_{a}$ .

Leite einen Term für den Flächeninhalt $A_{D}$ des Dreiecks her

Ermittle einen Wert von $a$ , für den die Dreiecksfläche die Größe $10 FE$ hat