Teil 1 ohne Hilfsmittel Analysis
- 1
Gegeben ist die Funktion mit der Definitionsmenge
Geben Sie die Koordinaten der Schnittpunkte des Graphen von mit den Koordinatenachsen an. (2 BE)
Widerlegen Sie die folgende Aussage: „Die Funktion ist umkehrbar.“ (3 BE)
Ermitteln Sie eine integralfreie Darstellung von . (3 BE)
- 2
Gegeben ist die Funktion mit der Definitionsmenge .
In der Abbildung ist ein Ausschnitt des Graphen der Funktion mit als Definitionsmenge zu sehen.
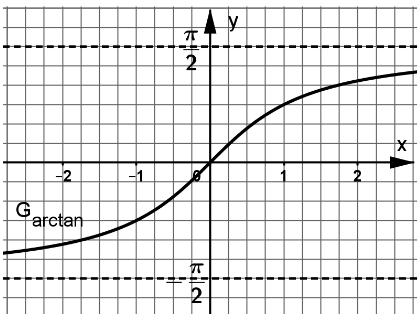
Für die nachfolgenden Teilaufgaben dürfen aus dieser Abbildung evtl. benötigte Funktionswerte entnommen werden.
Ermitteln Sie das Verhalten der Funktionswerte von an den Rändern von . (4 BE)
Berechnen Sie die Nullstelle von . (2 BE)
- 3
Gegeben ist die umkehrbare Funktion mit der Definitionsmenge . Ihre Umkehrfunktion wird mit bezeichnet.
Ermitteln Sie die Koordinaten des Schnittpunkts des Graphen von mit der -Achse. (4 BE)
Ermitteln Sie die Steigung der Tangente am Graphen von im Punkt .
Mögliches Teilergebnis: (4 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

