Aufgaben zum Zeichnen von Parabeln

1
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zeichne den Graphen der folgenden quadratischen Funktion. Lege dazu eine Wertetabelle an.
1. $f(x)=x^2+4x-5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=x^2+4x-5$
  Wertetabelle
  $x$
  -6
  -5
  -4
  -3
  -2
  -1
  0
  1
  2
  3
  $f(x)$
  7
  0
  -5
  -8
  -9
  -8
  -5
  0
  7
  16
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f(x)=x^2+2x+5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=x^2+2x+5$
  Wertetabelle
  $x$
  -4
  -3
  -2
  -1
  0
  1
  2
  3
  $f(x)$
  13
  8
  5
  4
  5
  8
  13
  20
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f(x)=-x^2+x+6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=-x^2+x+6$
  Wertetabelle
  $x$
  -3
  -2
  -1
  0
  1
  2
  3
  4
  $f(x)$
  -6
  0
  4
  6
  6
  4
  0
  -6
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f(x)=x^2-x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=x^2-x$
  Wertetabelle
  $x$
  -3
  -2
  -1
  0
  1
  2
  3
  4
  $f(x)$
  12
  6
  2
  0
  0
  2
  6
  12
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $f(x)=x^2-\frac19$
  
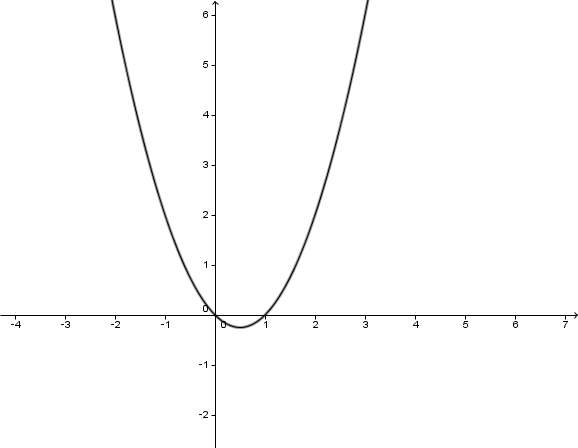
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=x^2-\frac19$
  Wertetabelle
  $x$
  -3
  -2
  -1
  0
  1
  2
  3
  4
  $f(x)$
  8,9
  3,9
  0,9
  -0,1
  0,9
  3,9
  8,9
  15,9
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $f(x)=\frac12x^2+2x+3$
  
  $f(x)=\frac12x^2+2x+3$
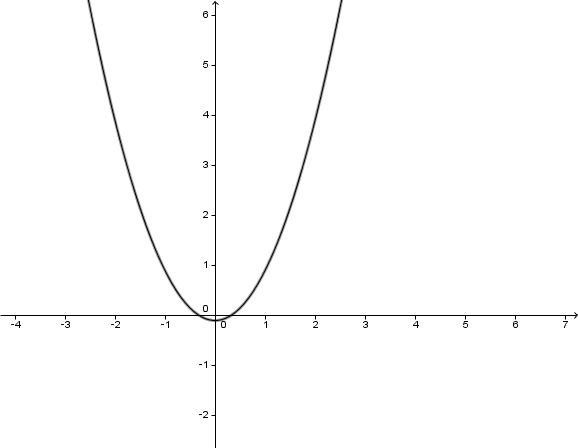
  Wertetabelle
  $x$
  -6
  -5
  -4
  -3
  -2
  -1
  0
  1
  2
  3
  $f(x)$
  9
  5,5
  3
  1,5
  1
  1,5
  3
  5,5
  9
  13,5
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $f(x)=-\frac13x^2+\frac23x+\frac53$
  
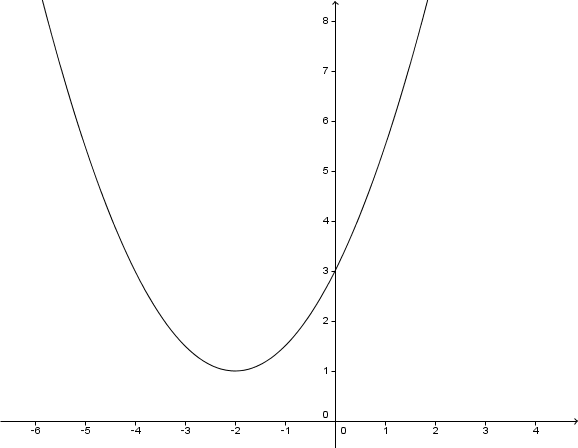
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=-\frac13x^2+\frac23x+\frac53$
  Wertetabelle
  $x$
  -4
  -3
  -2
  -1
  0
  1
  2
  3
  4
  5
  $f(x)$
  -6,3
  -3,3
  -1
  0,7
  1,7
  2
  1,7
  0,7
  -1
  -3,3
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. $f(x)=-2x^2+8x-11$
  
  $f(x)=-2x^2+8x-11$
  Wertetabelle
  $x$
  -1
  0
  1
  2
  3
  4
  5
  6
  $f(x)$
  -21
  -11
  -5
  -3
  -5
  -11
  -21
  -35
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9. $f(x)=3x^2-3x$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=3x^2-3x$
  Wertetabelle
  $x$
  -3
  -2
  -1
  0
  1
  2
  3
  4
  $f(x)$
  36
  18
  6
  0
  0
  6
  18
  36
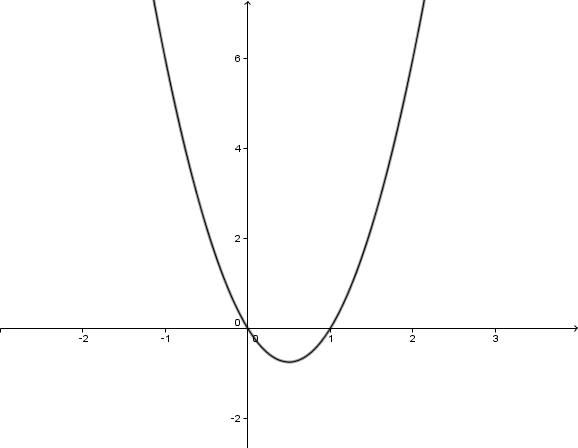
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10. $f(x)=\frac14x^2+\frac{11}2x+10$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichnen einer Parabel
  $f(x)=\frac14x^2+\frac{11}2x+10$
  Wertetabelle
  $x$
  -24
  -20
  -16
  -12
  -8
  -4
  0
  4
  $f(x)$
  22
  0
  -14
  -20
  -18
  -8
  10
  36
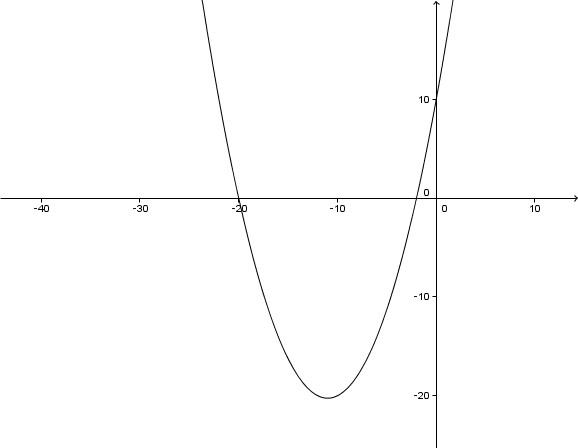
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
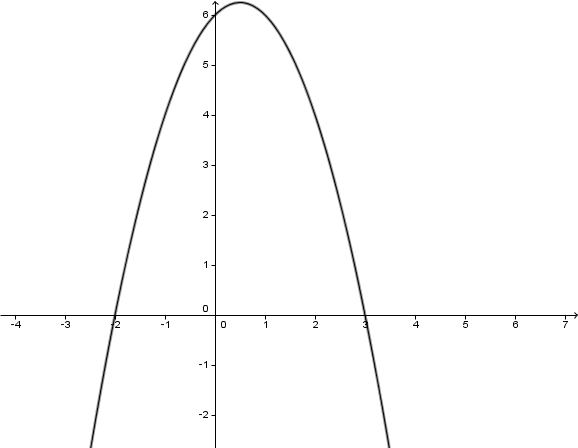
Die folgenden Abbildungen zeigen jeweils den Graphen einer Funktion der Form $f(x)=a\cdot x^2$ . Lies jeweils den Streckungsfaktor $a$ ab.
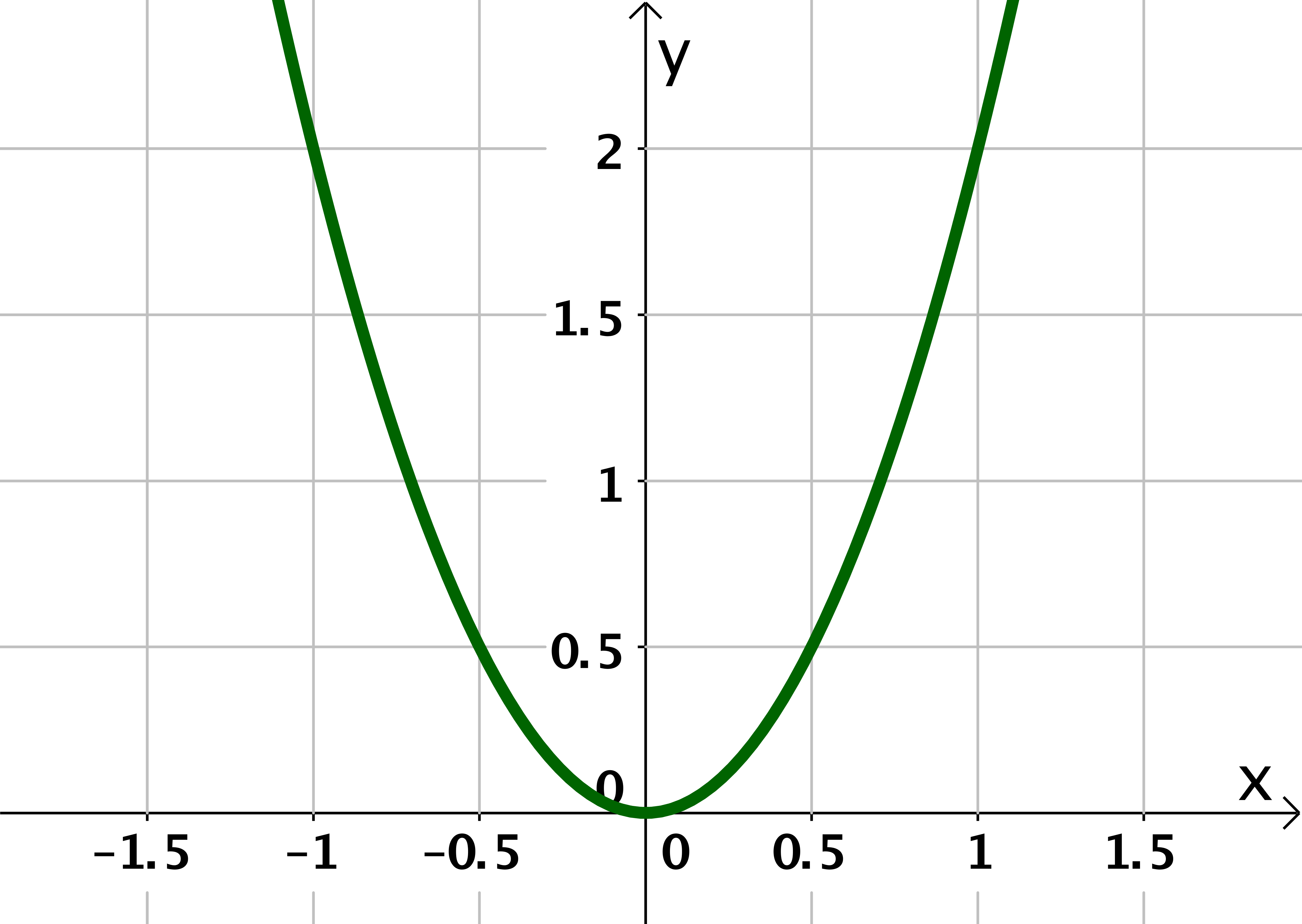
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabeln
  Finde allgemein eine zugehörige Funktionsgleichung, indem du einen Punkt des Graphen suchst, welcher sich gut ablesen lässt. Dessen $x$ - und $y$ -Koordinaten setzt du in die Funktion ein, um $a$ zu bestimmen.
  Lese einen geeigneten Punkt des Graphen ab.
  $A(1|2)$ liegt auf dem Graphen von $f$ .
  Setze dies in $f(x)=a \cdot x^2$ ein.
  $2=f(1)=a \cdot 1^2=a$
  Hier kannst du $a=2$ sofort ablesen und in $f$ einsetzen.
  $f(x)=2 \cdot x^2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
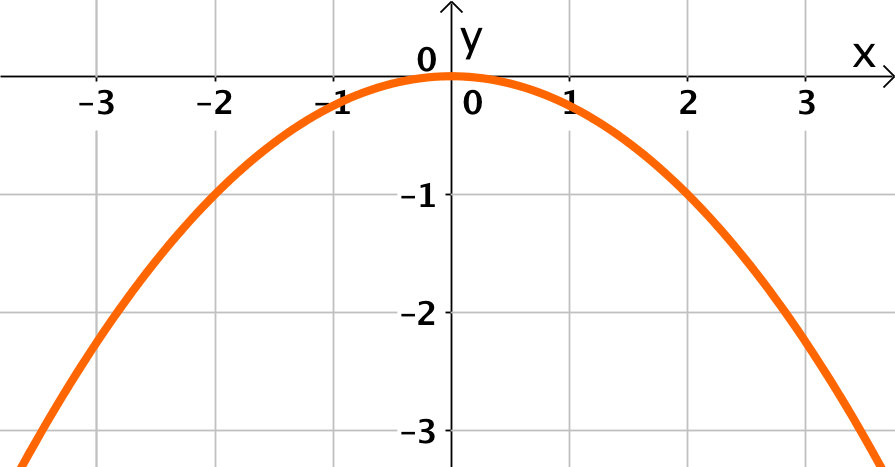
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabeln
  Finde allgemein eine zugehörige Funktionsgleichung, indem du einen Punkt des Graphen suchst, welcher sich gut ablesen lässt. Dessen $x$ - und $y$ -Koordinaten setzt du in die Funktion ein, um $a$ zu bestimmen.
  Lese einen geeigneten Punkt des Graphen ab.
  $A(2|-1)$ liegt auf dem Graphen von $f$ .
  Setze dies in $f(x)=a \cdot x^2$ ein.
  $-1=f(2)=a \cdot 2^2=4\cdot a$
  Hier kannst du $a=-\frac14$ sofort ablesen und in $f$ einsetzen.
  $f(x)=-\frac14 x^2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
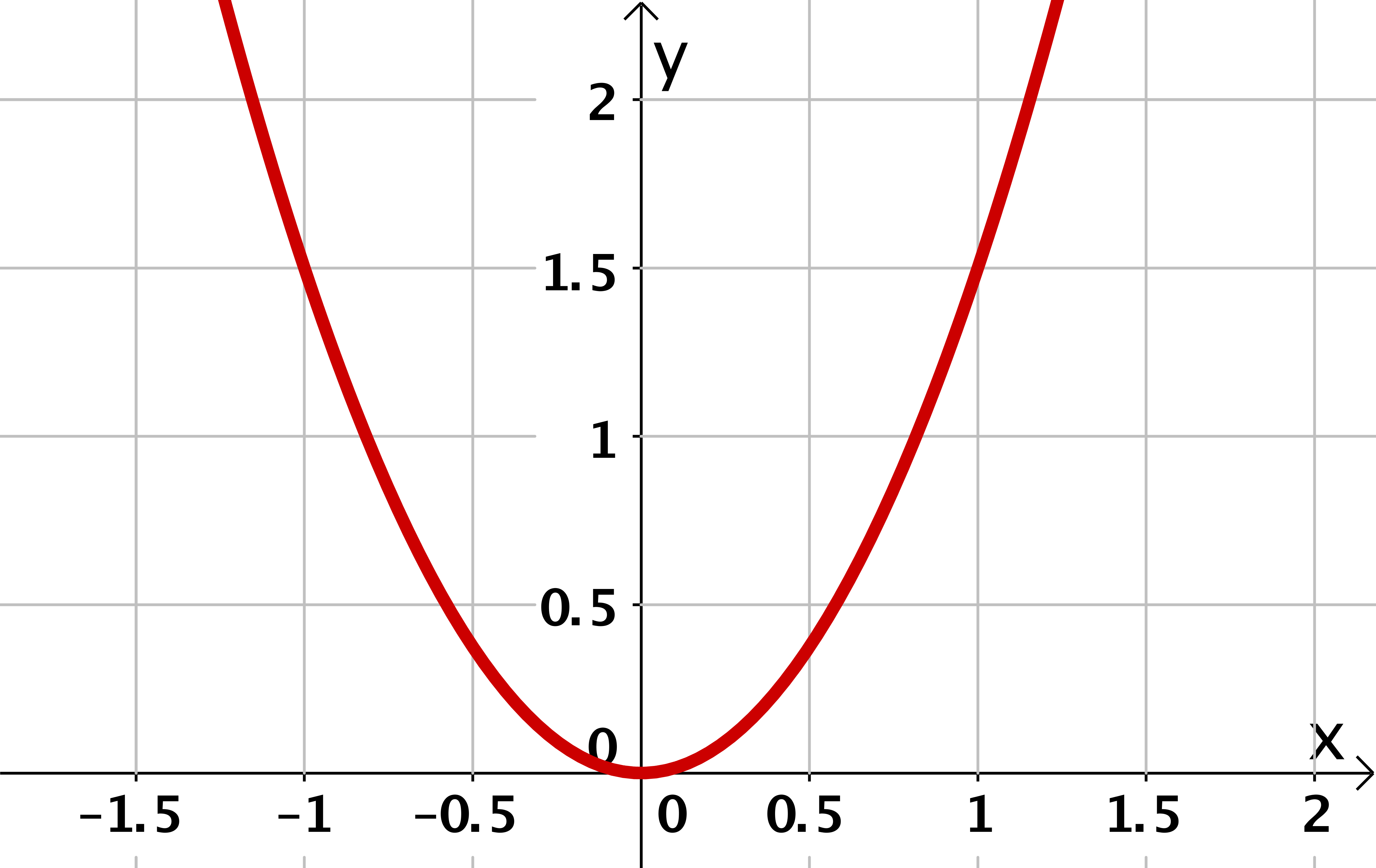
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabeln
  Finde allgemein eine zugehörige Funktionsgleichung, indem du einen Punkt des Graphen suchst, welcher sich gut ablesen lässt. Dessen $x$ - und $y$ -Koordinaten setzt du in die Funktion ein, um $a$ zu bestimmen.
  Lese einen geeigneten Punkt des Graphen ab.
  $A\left(1~|~1{,}5\right)$ liegt auf dem Graphen von $f$ .
  Setze dies in $f(x)=a \cdot x^2$ ein.
  $1{,}5=f(1)=a \cdot 1^2=a$
  Hier kannst du $a=1{,}5$ sofort ablesen und in $f$ einsetzen.
  $f(x)=1{,}5 \cdot x^2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
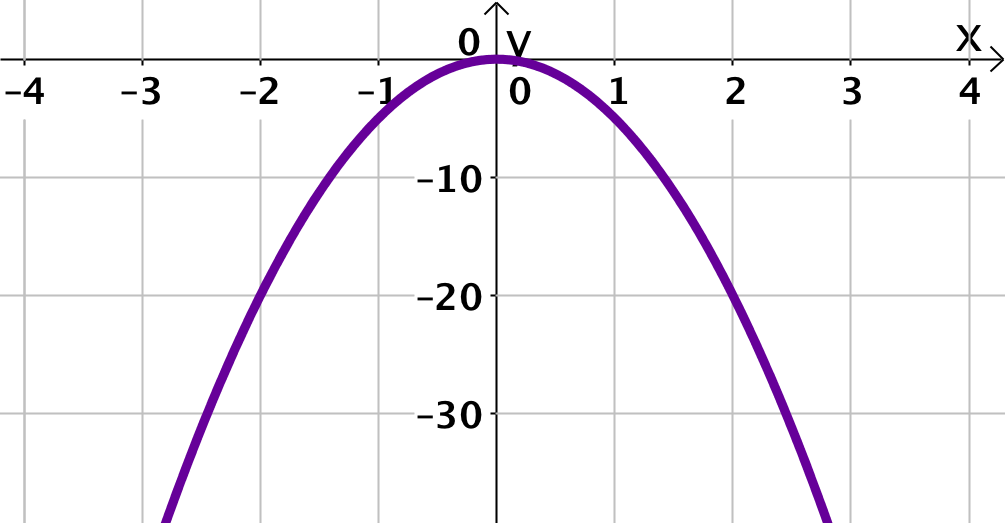
4. Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabeln
  Finde allgemein eine zugehörige Funktionsgleichung, indem du einen Punkt des Graphen suchst, welcher sich gut ablesen lässt. Dessen $x$ - und $y$ -Koordinaten setzt du in die Funktion ein, um $a$ zu bestimmen.
  Lese einen geeigneten Punkt des Graphen ab.
  $A\left(2~|-20\right)$ liegt auf dem Graphen von $f$ .
  Setze dies in $f(x)=a \cdot x^2$ ein.
  $-20=f(2)=a \cdot 2^2=4a$
  Hier kannst du $a=-5$ sofort ablesen und in $f$ einsetzen.
  $f(x)=-5 \cdot x^2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
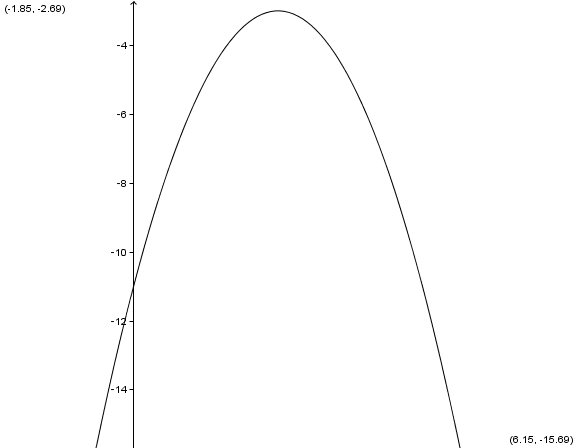
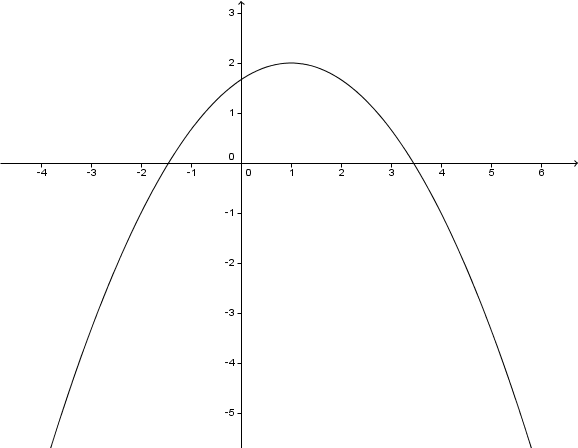
Wähle anhand der nebenstehenden Parabel die zugehörige Funktionsgleichung zu dem Graphen aus.
$f(x)=\frac{1}{4} (x-4)^2 +2$
$f(x)=\frac14 (x+4)^2+2$
$f(x)=4(x-4)^2+2$
$f(x)=\frac14 (x-2)^2+4$
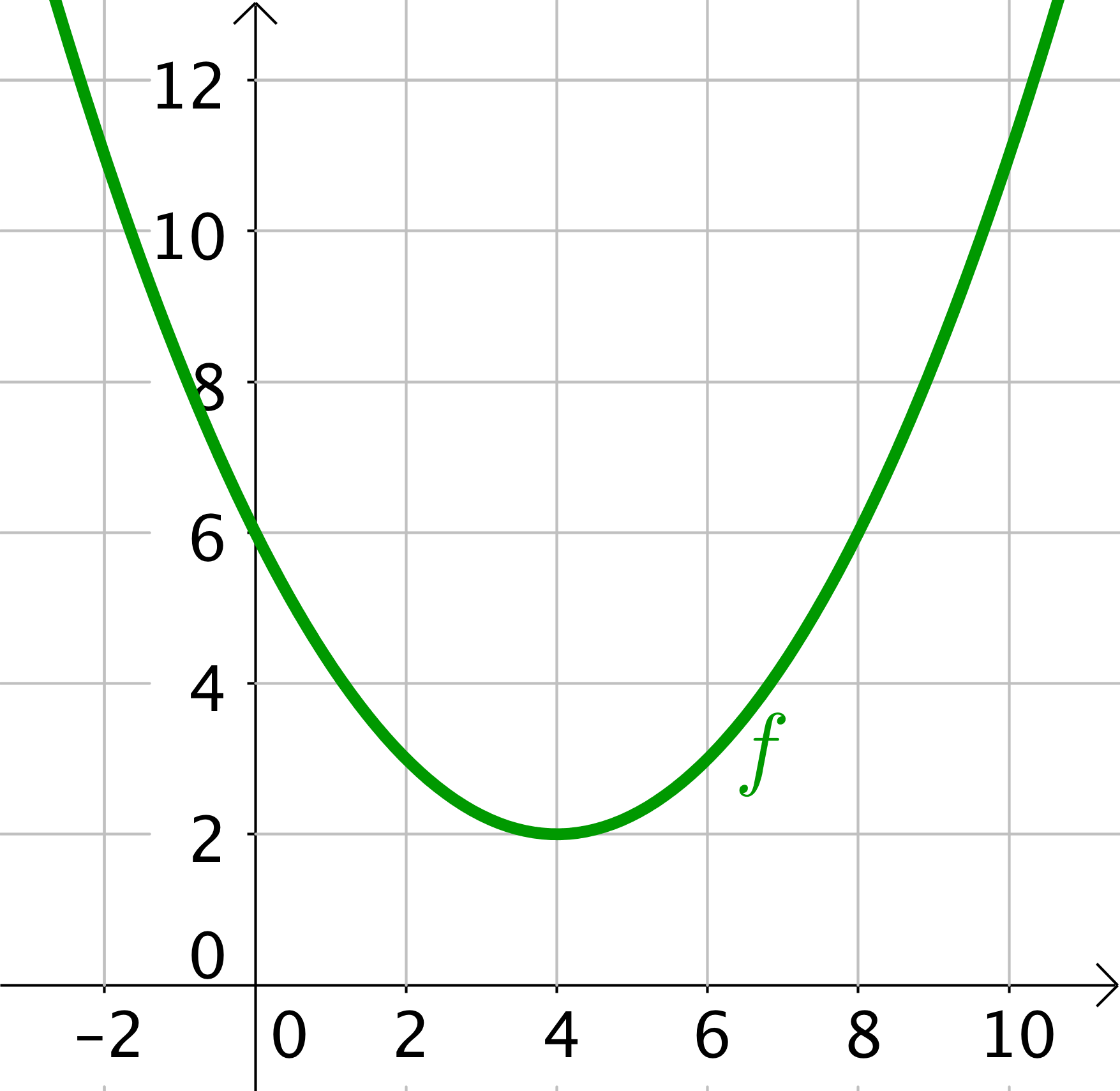
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einfluss der Parameter in der Scheitelform
Es ist hilfreich, dir im Vergleich zur vorliegenden Parabel zusätzlich die verschobene Normalparabel einzuzeichnen. Dann erhälst du eine Skizze wie hier. Damit siehst du schnell, ob die Parabel gestreckt, oder gestaucht wurde.
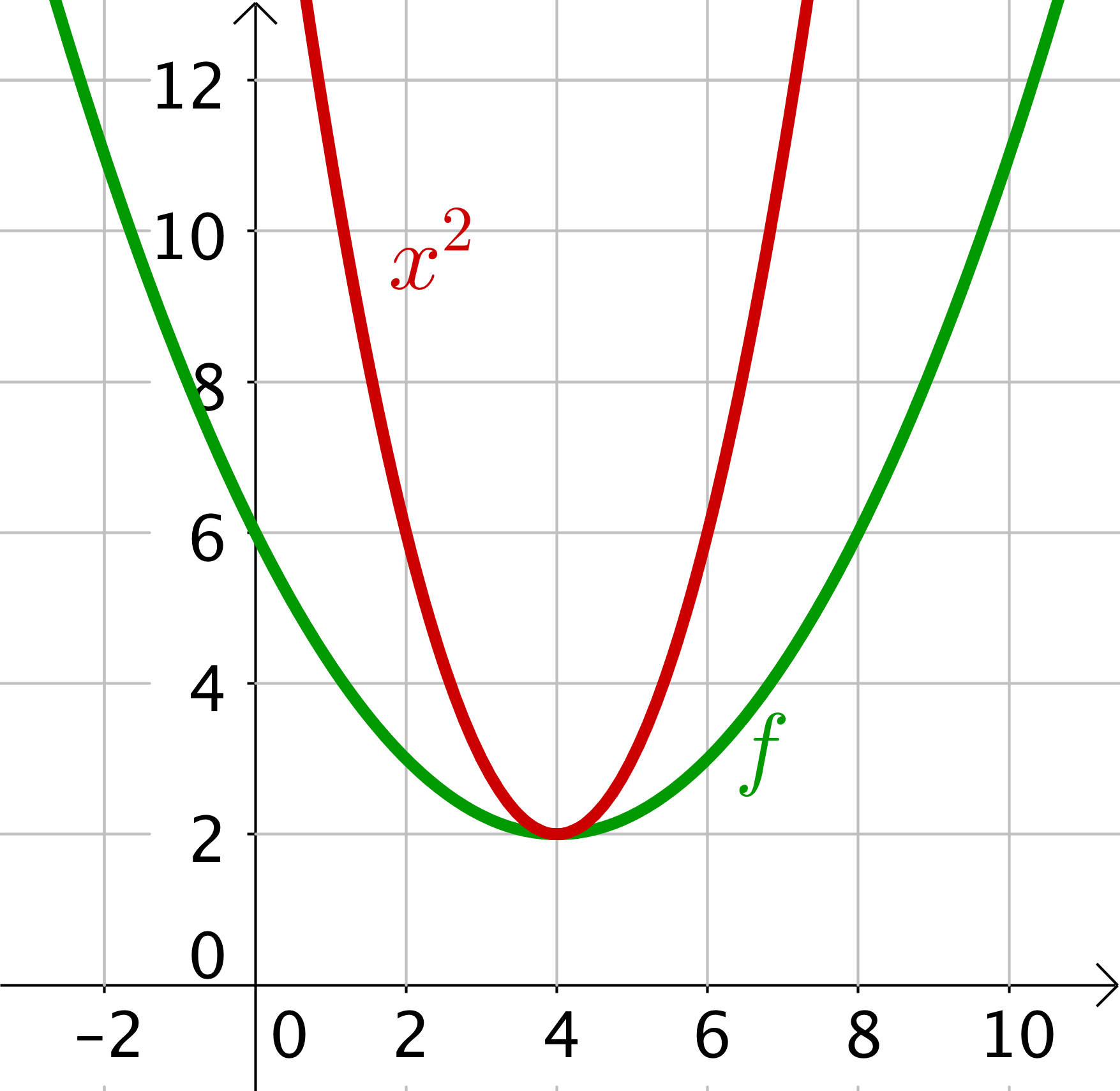
Den Scheitelpunkt kannst du sofort ablesen, dieser ist $S(4|2)$ und damit ist die Funktion in der Gestalt $f(x)=a(x-4)^2+2$ . Daher bleiben nur noch 2 Auswahlmöglichkeiten. Einmal mit $a=4$ und einmal mit $a=\frac{1}{4}$ . Hier macht nur letzteres Sinn, da die Parabel in y-Richung gestaucht wurde.
4
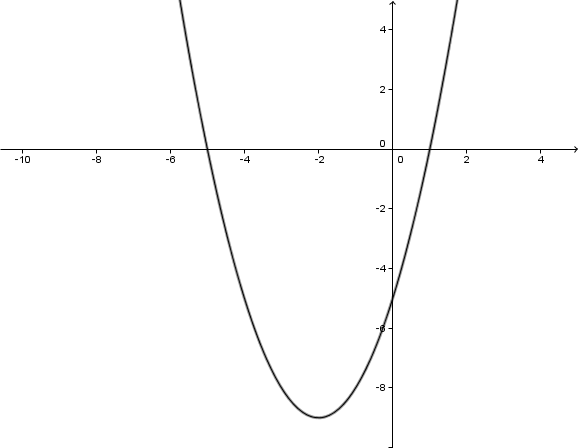
Wähle anhand der nebenstehenden Parabel die zugehörige Funktionsgleichung zu dem Graphen aus.
$f(x)=4 (x+6)^2-6$
$f(x)=\frac{1}{4}(x+6)^2-6$
$f(x)=4(x-6)^2-6$
$f(x)=4(x-6)^2+6$
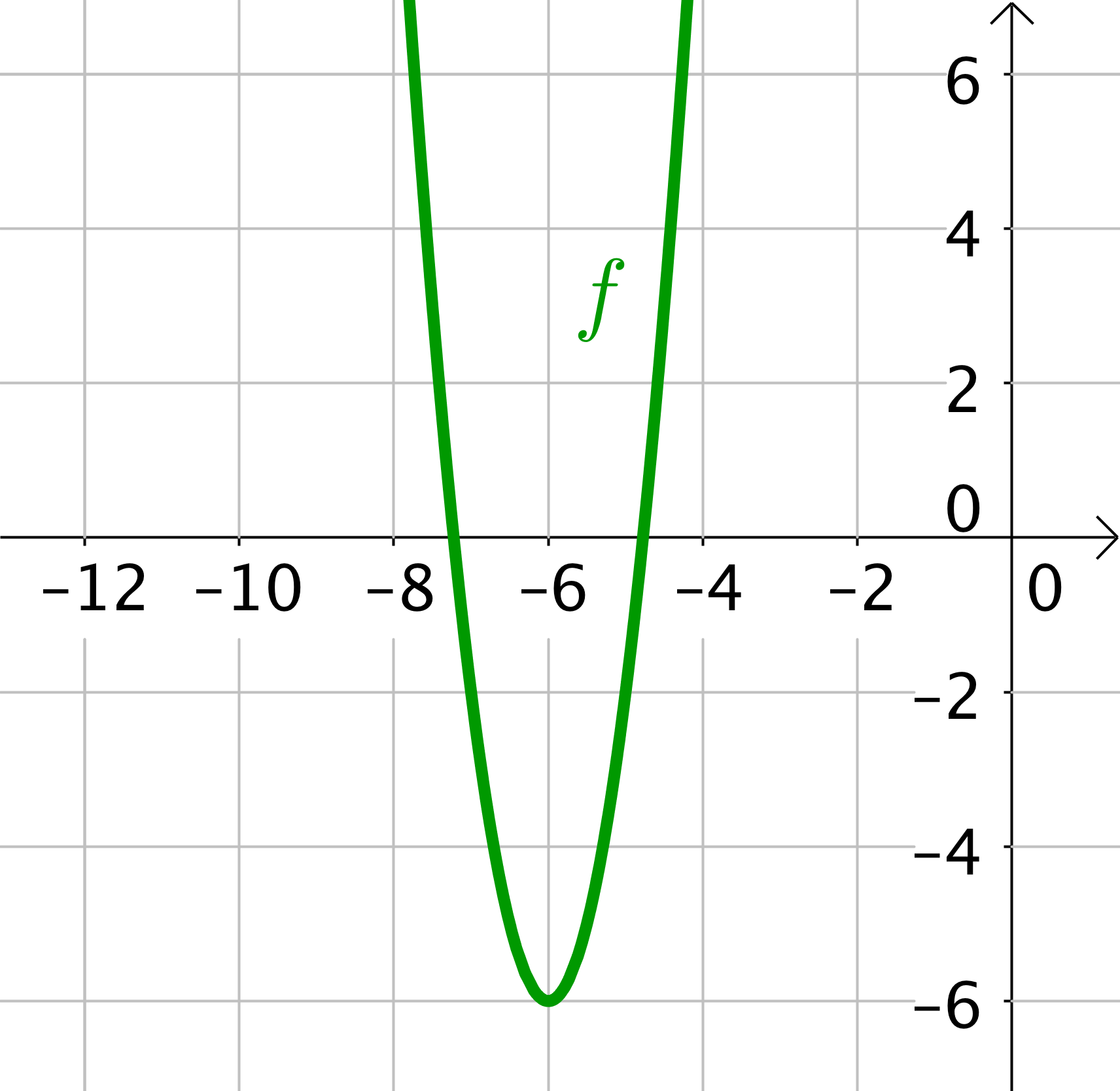
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einfluss der Parameter in der Scheitelform
Es ist hilfreich, dir im Vergleich zur vorliegenden Parabel zusätzlich die verschobene Normalparabel einzuzeichnen. Dann erhälst du eine Skizze wie hier. Damit erkennst du, ob die Parabel gestreckt oder gestaucht wird.
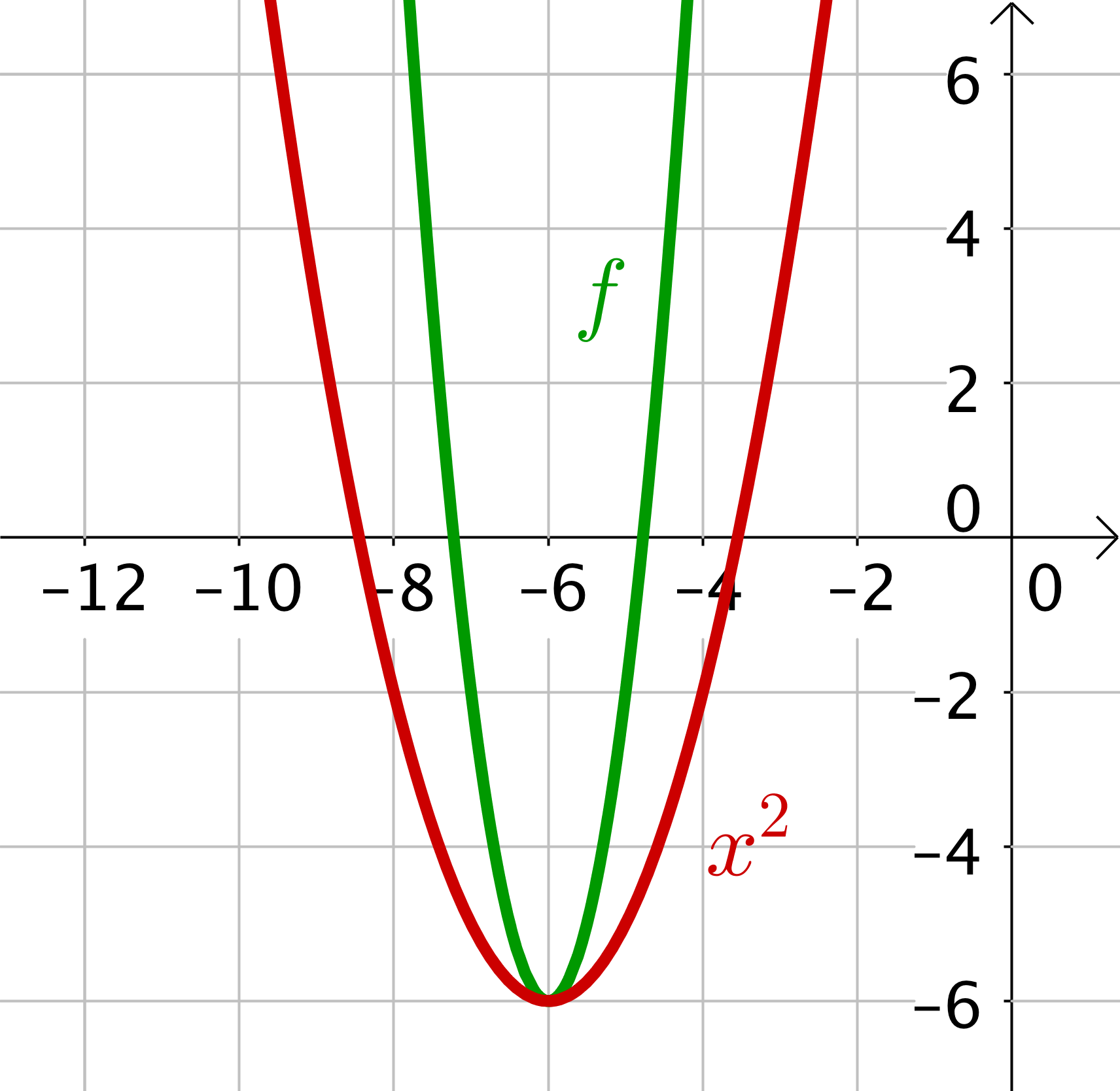
Den Scheitelpunkt kannst du sofort ablesen, dieser ist $S(-6|-6)$ und damit ist die Funktion in der Gestalt $f(x)=a(x+6)^2-6.$ Daher bleiben nur noch 2 Auswahlmöglichkeiten. Einmal mit $a=4$ und einmal mit $a=\frac14.$ Hier macht nur ersteres Sinn, da die Parabel in y-Richtung gestreckt wurde.
5
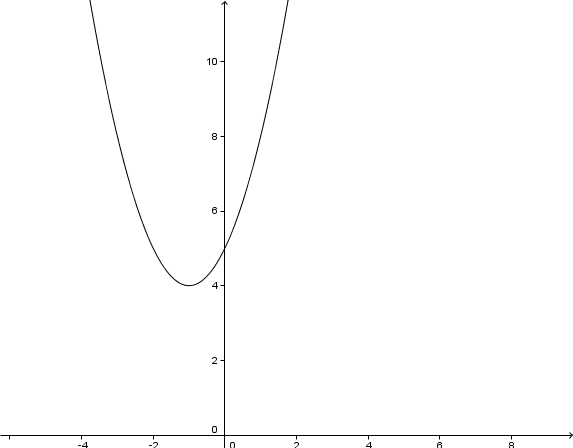
Wähle anhand der nebenstehenden Parabel die zugehörige Funktionsgleichung zu dem Graphen aus.
$f(x)=-\frac15 (x-10)^2-5$
$f(x)=-5(x-10)^2-5$
$f(x)=\frac15 (x-10)^2 -5$
$f(x)=-\frac15 (x+10)^2-5$
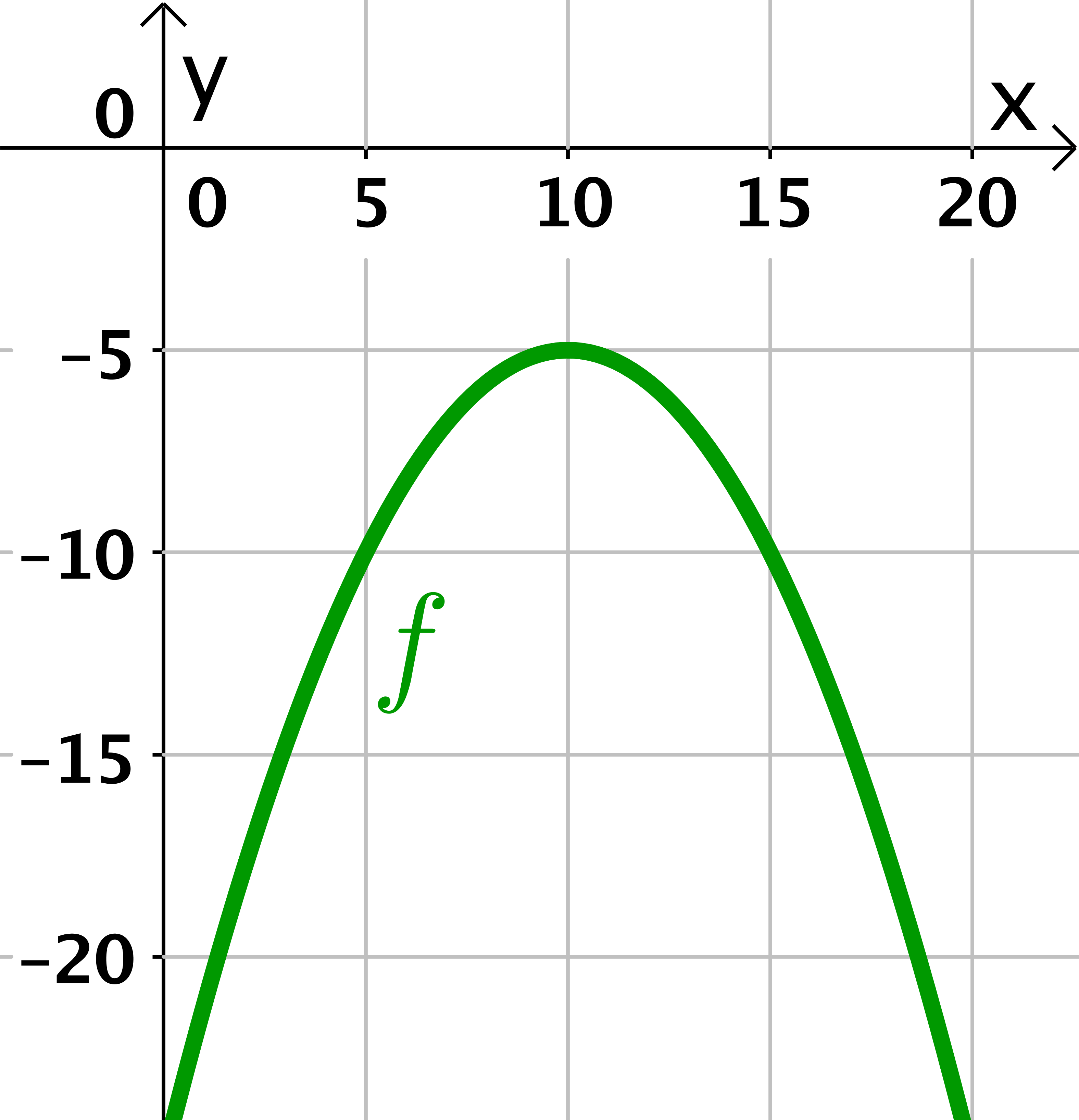
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einfluss der Parameter in der Scheitelform
Es ist hilfreich, dir im Vergleich zur vorliegenden Parabel zusätzlich die verschobene Normalparabel einzuzeichnen. Dann erhälst du eine Skizze wie hier. Damit erkennst du, ob die Parabel gestreckt oder gestaucht wird.
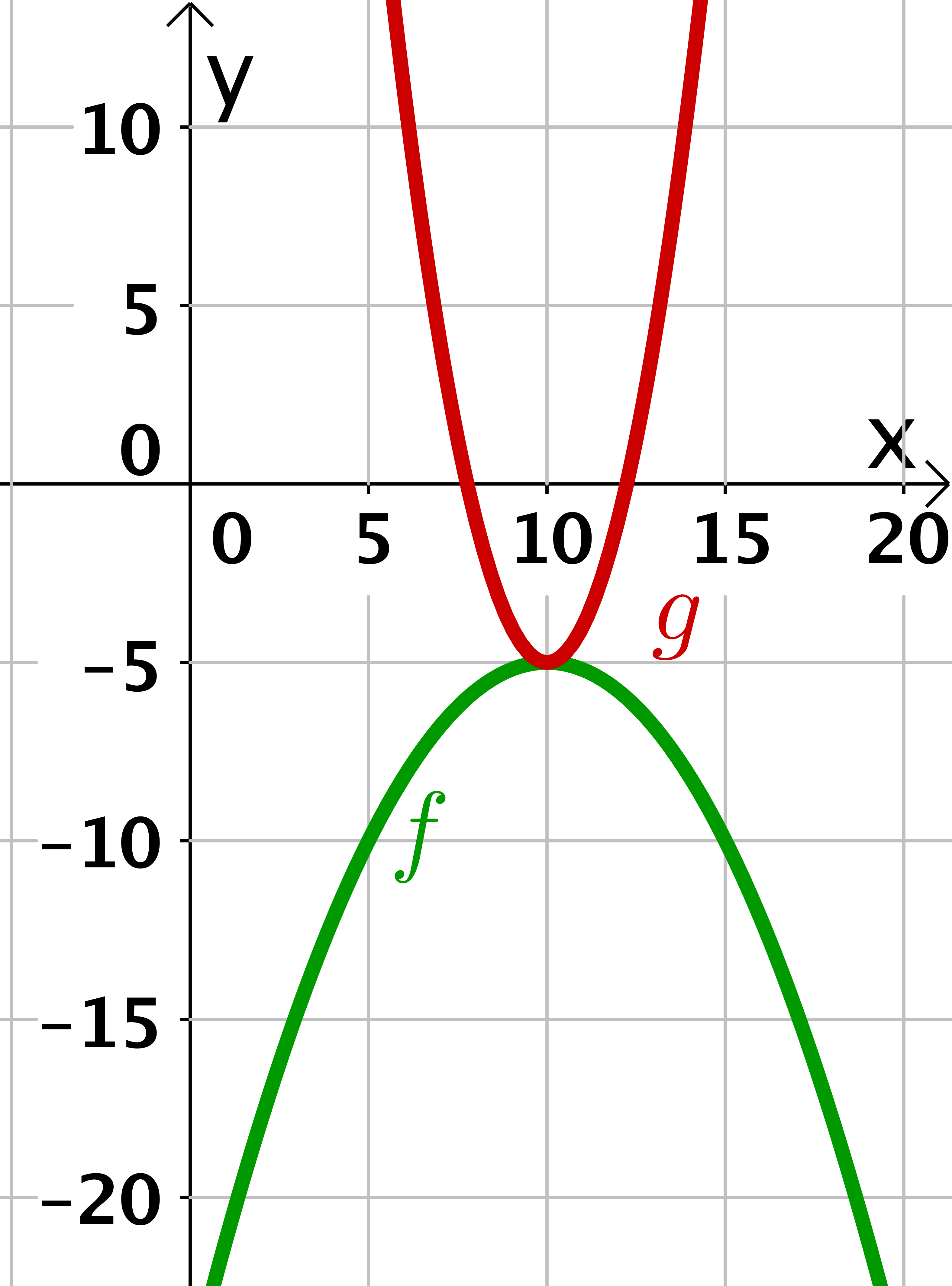
Den Scheitelpunkt kannst du sofort ablesen, dieser ist $S(10|-5)$ und damit ist die Funktion in der Gestalt $f(x)=a(x-10)^2-5.$ Daher bleiben nur noch 3 Auswahlmöglichkeiten. Diese sind $a=\frac15$ , $a=-\frac15$ und $a=-5$ . Hier macht nur zweiteres Sinn, da die Parabel
zum einen nach unten geöffnet ist und daher der Parameter $a$ negativ ist
zum anderen in y-Richtung gestaucht wird und daher $|a|<1$ ist

$x$	-6	-5	-4	-3	-2	-1	0	1	2	3
$f(x)$	7	0	-5	-8	-9	-8	-5	0	7	16

$x$	-4	-3	-2	-1	0	1	2	3
$f(x)$	13	8	5	4	5	8	13	20

$x$	-3	-2	-1	0	1	2	3	4
$f(x)$	-6	0	4	6	6	4	0	-6

$x$	-3	-2	-1	0	1	2	3	4
$f(x)$	12	6	2	0	0	2	6	12

$x$	-3	-2	-1	0	1	2	3	4
$f(x)$	8,9	3,9	0,9	-0,1	0,9	3,9	8,9	15,9

$x$	-6	-5	-4	-3	-2	-1	0	1	2	3
$f(x)$	9	5,5	3	1,5	1	1,5	3	5,5	9	13,5

$x$	-4	-3	-2	-1	0	1	2	3	4	5
$f(x)$	-6,3	-3,3	-1	0,7	1,7	2	1,7	0,7	-1	-3,3

$x$	-1	0	1	2	3	4	5	6
$f(x)$	-21	-11	-5	-3	-5	-11	-21	-35

$x$	-3	-2	-1	0	1	2	3	4
$f(x)$	36	18	6	0	0	6	18	36

$x$	-24	-20	-16	-12	-8	-4	0	4
$f(x)$	22	0	-14	-20	-18	-8	10	36

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Zeichnen von Parabeln

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Wertetabelle

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?