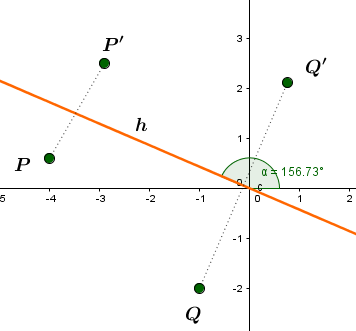
Der Bildpunkt entsteht durch Spiegelung des Urpunktes an einer Ursprungsgeraden .Gib die Gleichung der Spiegelachse , die Abbildungsgleichung und die Koordinaten von an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelachse berechnen
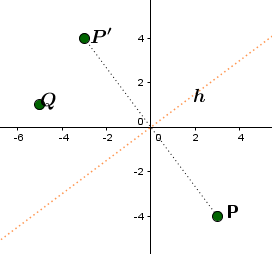
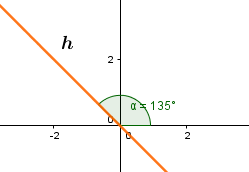
Skizze:
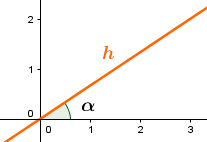
Um die Gleichung der Spiegelachse zu bestimmen, musst du zuerst den Schnittwinkel der Spiegelachse mit der x-Achse berechnen. Dazu benuzt du die Abbildungsgleichung, setzt und ein und löst nach auf.
Hier bietet sich die Koordinatenform an:
Setze in ein und löse nach auf.
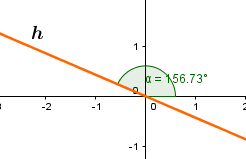
Du hast also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Mit dieser Information kannst du auf die Steigung der Geraden schließen und somit die Geradengleichung aufstellen.
Nachdem du die Gleichung der Spiegelachse bestimmt hast, musst du noch die Abbildungsgleichung und den Bildpunkt angeben bzw. berechnen.
Abbildungsgleichung in Koordinatenform:
Spiegelung von
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelachse berechnen
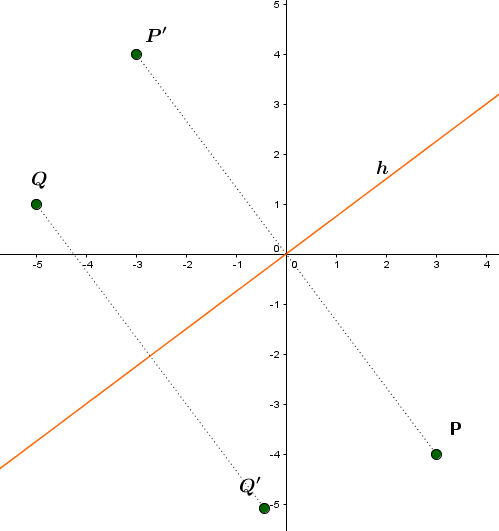
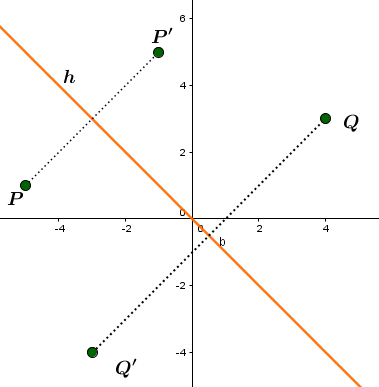
Skizze:
Um die Gleichung der Spiegelachse zu bestimmen, musst du zuerst den Schnittwinkel der Spiegelachse mit der x-Achse berechnen. Dazu benuzt du die Abbildungsgleichung, setzt und ein und löst nach auf.
Hier bietet sich die Koordinatenform an:
Setze in ein und löse nach auf.
in :
Du hast also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Mit dieser Information kannst du auf die Steigung der Geraden schließen und somit die Geradengleichung aufstellen.
Nachdem du die Gleichung der Spiegelachse bestimmt hast, musst du noch die Abbildungsgleichung und den Bildpunkt angeben bzw. berechnen.
Abbildungsgleichung in Koordinatenform:
Spiegelung von
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelachse berechnen
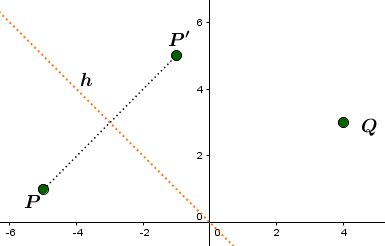
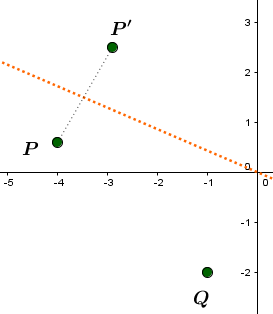
Skizze:
Um die Gleichung der Spiegelachse zu bestimmen, musst du zuerst den Schnittwinkel der Spiegelachse mit der x-Achse berechnen. Dazu benuzt du die Abbildungsgleichung, setzt und ein und löst nach auf.
Hier bietet sich die Koordinatenform an:
Setze in ein und löse nach auf.
in :
Du hast also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Mit dieser Information kannst du auf die Steigung der Geraden schließen und somit die Geradengleichung aufstellen.
Nachdem du die Gleichung der Spiegelachse bestimmt hast, musst du noch die Abbildungsgleichung und den Bildpunkt angeben bzw. berechnen.
Abbildungsgleichung in Koordinatenform:
Spiegelung von
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?