Aufgaben zur zentrischen Streckung
- 1
Strecke den Punkt um den Faktor um den Ursprung
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Alternative 1: Lösung in Koordinatenform:
Setze den Faktor in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Faktor in die Matrix ein.
Setze die Koordinaten des Punkte .
Führe Matrix-Vektor-Multiplikation durch.
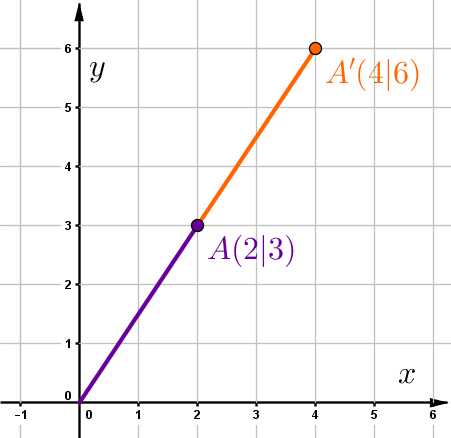
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Alternative 1: Lösung in Koordinatenform:
Setze den Faktor in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Faktor in die Matrix ein.
Setze die Koordinaten des Punkte .
Führe die Matrix-Vektor-Multiplikation durch.
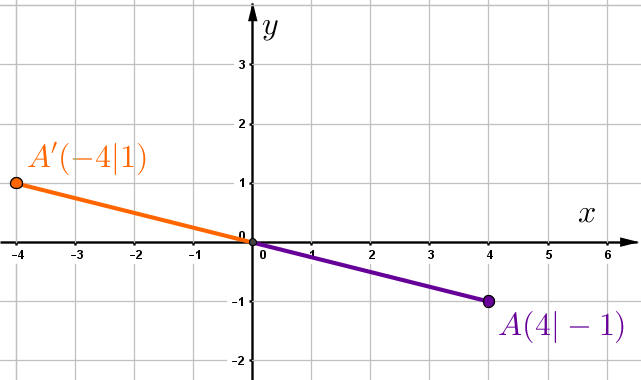
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Alternative 1: Lösung in Koordinatenform:
Setze den Faktor in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Faktor in die Matrix ein.
Setze die Koordinaten des Punkte A=(5|1).
Führe die Matrix-Vektor-Multiplikation durch.
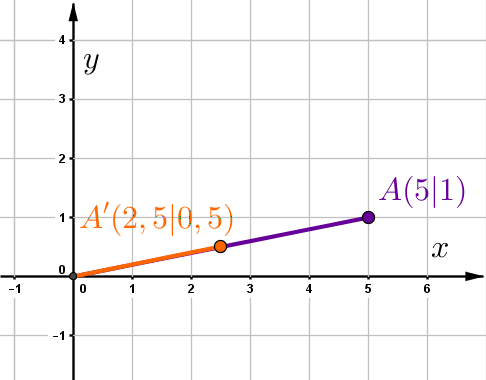
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Alternative 1: Lösung in Koordinatenform:
Setze den Faktor in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Faktor in die Matrix ein.
Setze die Koordinaten des Punkte .
Führe die Matrix-Vektor-Multiplikation durch.
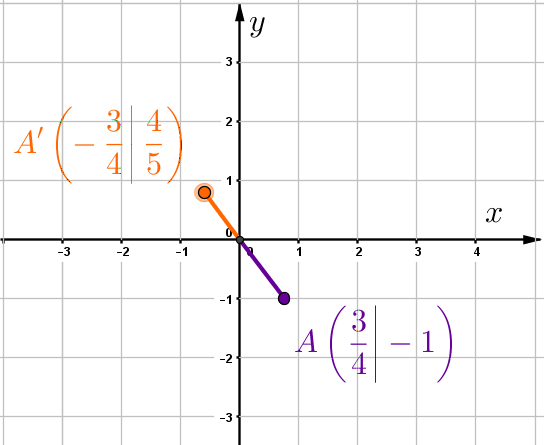
Hast du eine Frage oder Feedback?
- 2
Strecke die Gerade, die durch die Gleichung gegeben ist, um den Faktor .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Wähle zwei Punkte auf der Geraden, zum Beispiel den - und den -Achsenabschnitt.
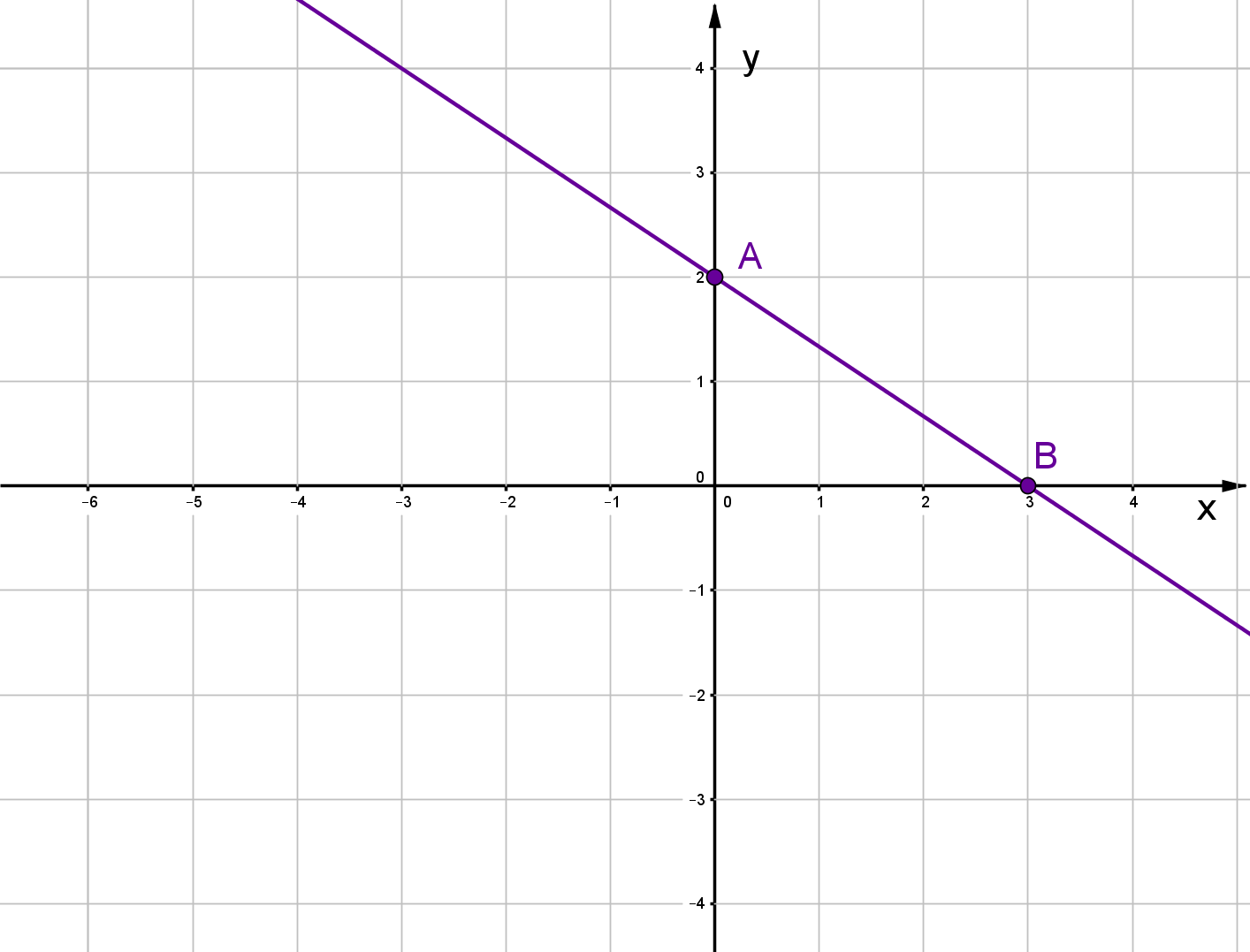
und
Strecke die Punkte und um den Faktor .
Alternative 1: Berechnung in Koordinatenform:
Setze den Faktor in das Gleichungssystem ein.
Damit sind die gestreckten Punkte und .
Alternative 2: Berechnung in Matrixform:
Setze die Koordinaten der Punkte und in die Vektoren ein.
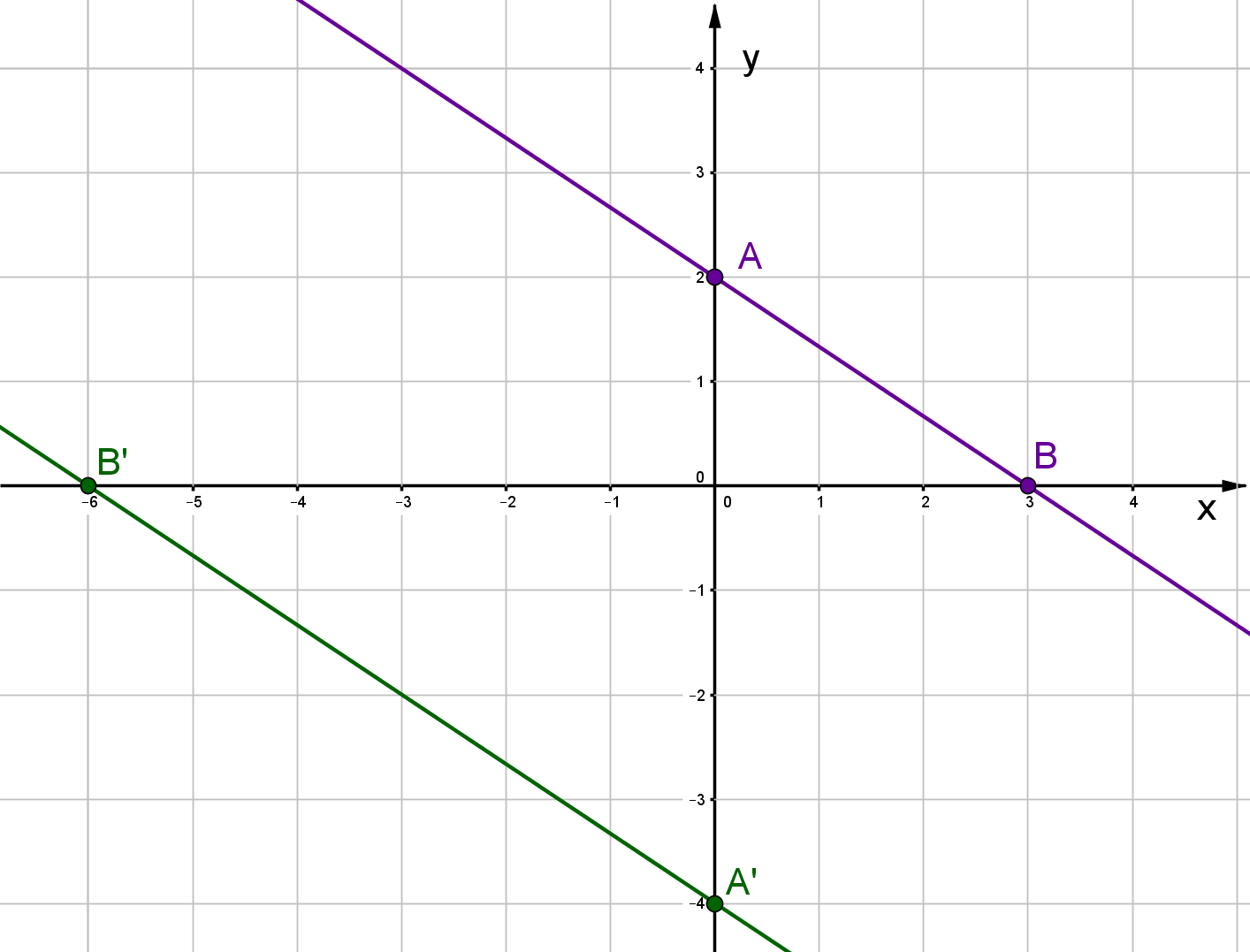
Damit sind die gestreckten Punkte und .
Aufstellen der Geradengleichung:
Den -Achsenabschnitt kannst du von dem Punkt ablesen.
Die Steigung kannst du durch die Koordinaten der Punkte und bestimmen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
