Einführung in die Methode des Felder-Abstreichens

1 Zweck des Felder-Abstreichens (1|3)

"Felder abstreichen"? Was ist denn das?

Und wozu brauche ich so was?

Die Methode des Felder-Abstreichens dient dazu, dass man sich einen ungefähren Überblick über

den Verlauf eines Funktionsgraphen verschafft,
wenn man nur den Funktionsterm gegeben hat.

Zum Beispiel hast du diesen Funktionsterm gegeben:

\displaystyle f(x)=\frac{1}{6} x^4-\frac{1}{6}x^3-x^2

*Und wie sieht jetzt dazu der Graph aus?*

2 Zweck des Felder-Abstreichens (2|3)

Moment, langsam, langsam: Auch beim Felder-Abstreichen kannst du nicht sofort den Graphen hinzeichnen, sondern musst zunächst einmal etwas rechnen:

Zum Beispiel die Nullstellen der Funktion - die musst du wissen, ehe du mit dem Zeichnen anfangen kannst.

Hm, na ja… - das klingt nach einer Menge Arbeit.

Lohnt sich das denn überhaupt? Was bringt mir das Felder-Abstreichen denn eigentlich?

Soll ich da nicht besser einfach eine Wertetabelle machen und den Graph so genau wie möglich zu zeichnen versuchen?

Bei einer Wertetabelle weißt du nie ganz sicher, ob du sie wirklich im "interessanten" Bereich der Funktion angelegt hast, und ob die Schrittweite klein genug war.

Das Felder-Abstreichen liefert dir die Information darüber,

in welchen Bereichen der Graph oberhalb
und in welchen er unterhalb der x-Achse verläuft.

Das reicht oft schon aus, um einen Eindruck vom ungefähren Verlauf des Graphen zu bekommen - und mehr braucht man oft auch nicht.

3 Zweck des Felder-Abstreichens (3|3)

Und damit - also mit dem Felder-Abstreichen - spart man sich dann die Wertetabelle? Klingt cool!

Dann sag mir doch bitte, wie dieses Felder-Abstreichen geht!

Also: Du berechnest die Nullstellen, grenzt die Bereiche ab, ermittelst für jeden Bereich das Vorzeichen….

Halt, Stopp!!! Das geht mir VIEL zu schnell!

Kannst du mir das vielleicht doch lieber erst mal an einem Beispiel erklären?

4 Beispiel

Ein Beispiel? - Na klar!

Dann nehmen wir doch einfach gleich die Funktion $f$ von vorhin:

\displaystyle f:x\mapsto f(x)=\frac{1}{6} x^4-\frac{1}{6}x^3-x^2

- und für die führen wir gemeinsam das Felder-Abstreichen durch!

Ja cool, gute Idee!

Warte nur noch einen Augenblick, ich hol' mir nur schnell noch Stift und Papier - und den Taschenrechner!

Und dann geht's los!

Und du - ja du, du da draußen vor dem Bildschirm, dich meine ich, genau dich - möchtest du nicht auch mitmachen?

5 Erster Schritt: Nullstellen bestimmen (1| )

Okay, der Funktionsterm ist:

\displaystyle f(x)=\frac{1}{6} x^4-\frac{1}{6}x^3-x^2

Und wie fange ich jetzt an?

Als Erstes brauchst du die Nullstellen der Funktion, also

diejenigen x-Werte, für die $f (x) = 0$ wird.

Das sind dann nämlich genau die Stellen, an denen der Graph die x-Achse schneidet.

Ich zeichne dir hier mal als Beispiel irgendeinen Graphen - schau mal, so vielleicht:

- und rot markiert habe ich dir die Nullstellen der Funktion.

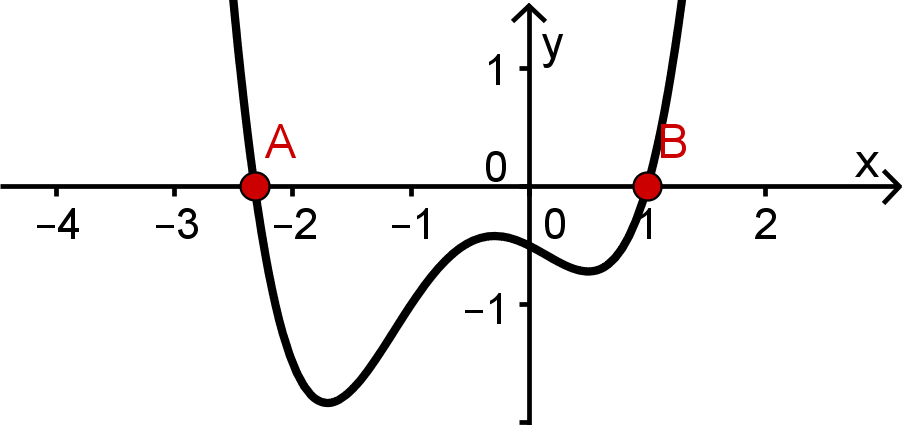
Ohne die Nullstellen der Funktion können wir nicht mit dem Felder-Abstreichen anfangen.

6 Erster Schritt: Nullstellen bestimmen (2| )

Um die Nullstellen zu erhalten, musst du immer

den Funktionsterm gleich 0 setzen.

Dadurch erhältst du eine Gleichung der Form $f (x) = 0$ . Und aus dieser Gleichung musst du dann

x herausfinden.

Wie das geht, hängt natürlich von der Funktion ab.

Aber - wie soll ich das denn machen?

Ist das denn bei jeder Funktion immer ganz anders?

Eine allgemeine Regel, die immer in der gleichen Weise funktioniert, gibt es nicht. Aber es gibt natürlich schon verschiedene Ansätze - und Regeln für bestimmte Fälle.

Schau doch mal ins Internet zu Serlo: Da gibt es einen eigenen Artikel zum Thema "Nullstellen berechnen". Und sogar noch einen Kurs "Berechnungsmethoden - Nullstellen von Polynomfunktionen"

7 Nullstellen im Beispiel

Die Nullstellen der Funktion $f$ sind:

$x_{1} = 0$ (das ist eine doppelte Nullstelle)

\displaystyle x_2=3

\displaystyle x_3=-2

Wow! Wie hast du denn das so schnell herausgekriegt?

Äh, ja… also, wenn ich ehrlich bin: Ich hab die Aufgabe von Serlo, und da steht auch eine Lösung dazu:

Laden