Bestimme die Funktionsgleichung zu folgenden Graphen:
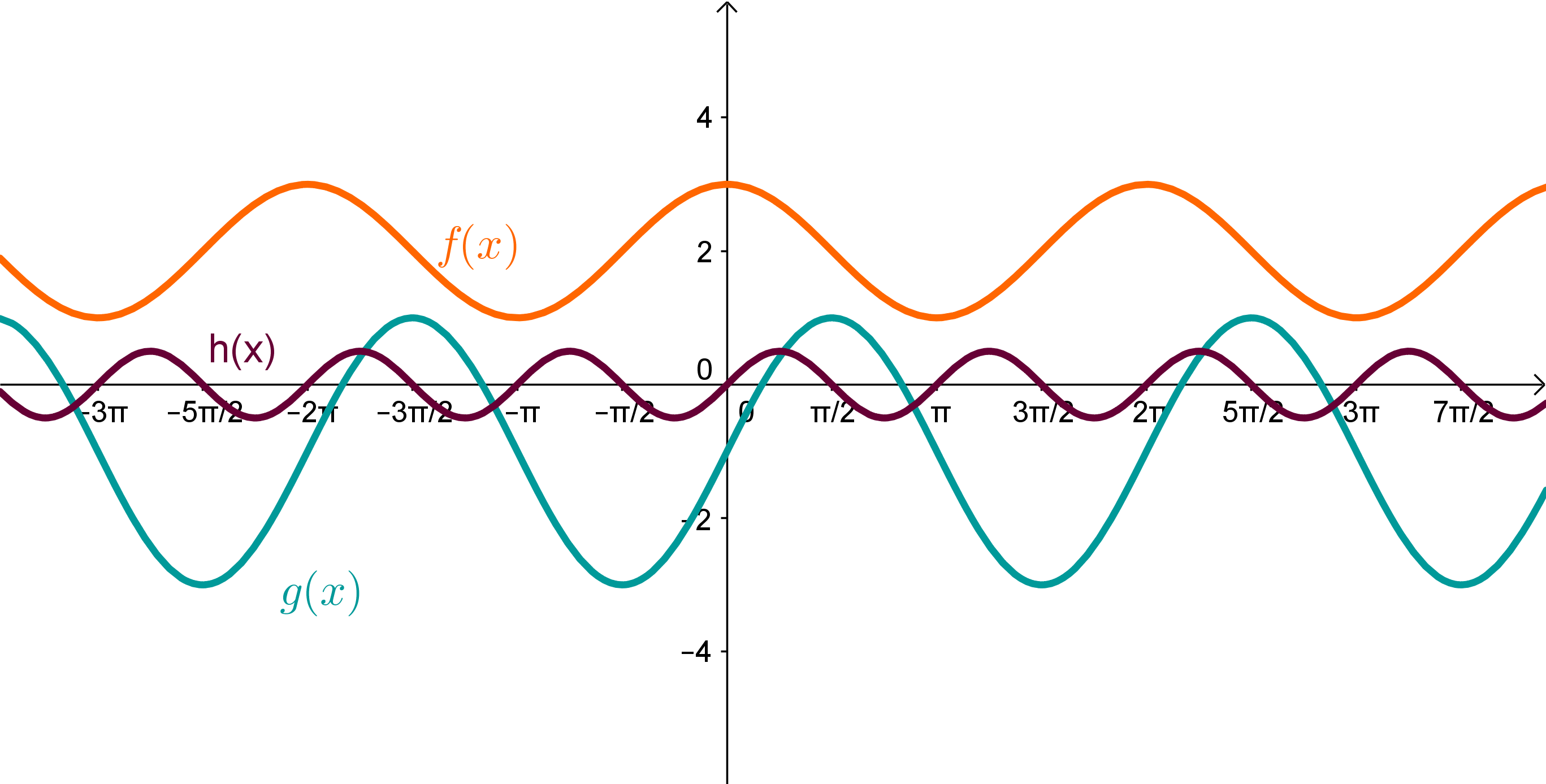
Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktionen
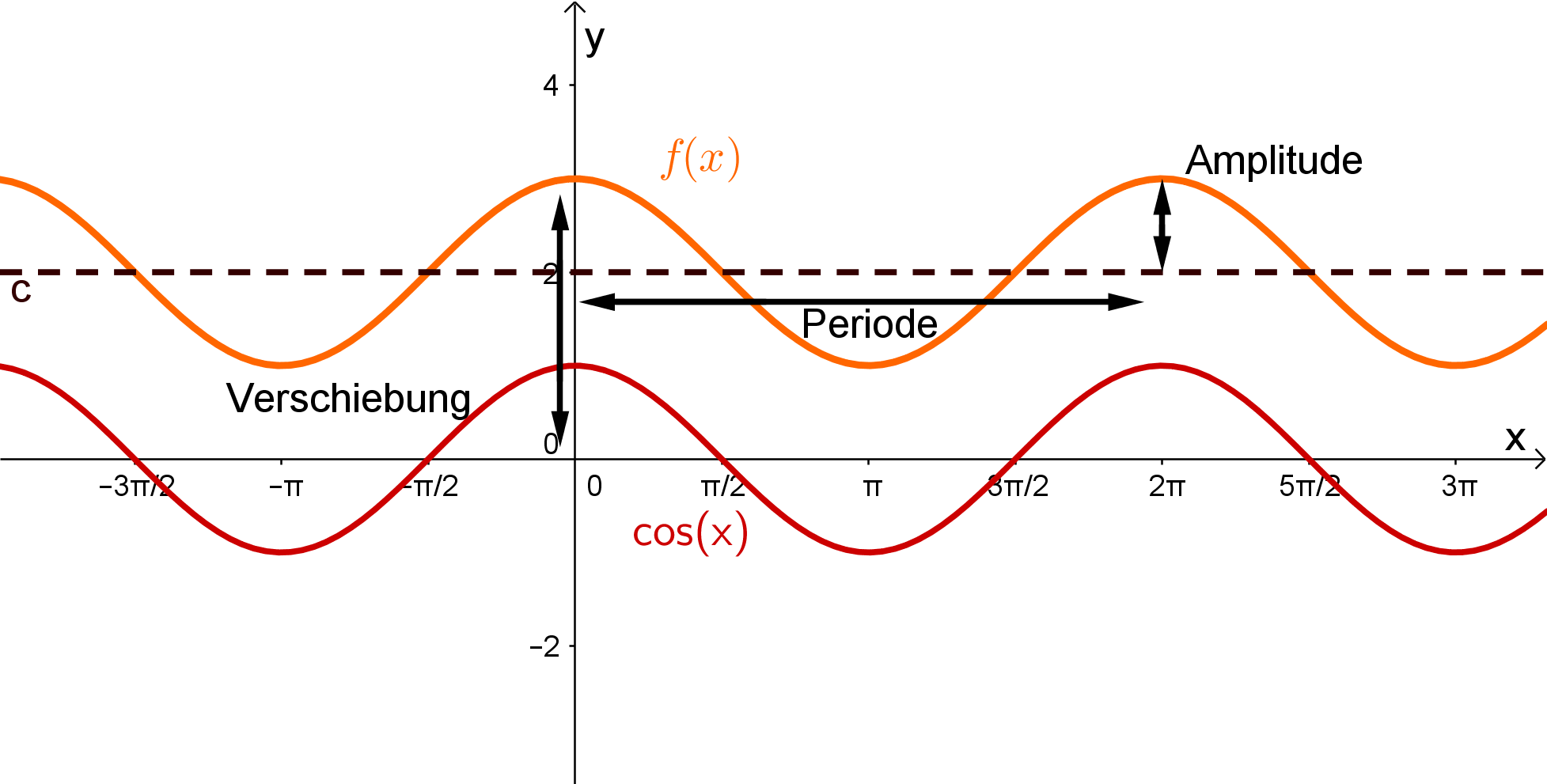
Lösung für die Funktion :
Aufgrund der Achsensymmertrie muss es sich um eine Kosinus-Funktion handeln.
Du kannst die Kosinus-Funktion verschieben und strecken, mit der allgemeinen Funktionsgleichung: .
Betrachtest du die Amplitude der Funktion, siehst du das diese beträgt, also genau so groß wie bei der normalen Kosinus-Funktion , dass heißt für die allgemeine Funktionsgleichung, das den Wert haben muss, weil man die Amlitupde der Funktion nicht verändert.
Ebenfalls siehst du, dass der Graph der gesuchten Funktion die selbe Periode wie die Funktion, das bedeutet, aus der allgemeinen Form muss den Wert haben.
Nachdem die gesuchte Funktion auch nicht nach rechts oder links verschoben wurde,muss der Wert von aus der allgemeinen Form sein.
Jetzt musst du also nur noch die Verschiebung des Graphen der gesuchten Funktionnach oben betrachten. Der Graph der gesuchten Funktion wurde um nach oben verschoben, das heißt, aus der alllgemeinen Form hat den Wert .
Fasst du nun alle Werte der Variablen zusammen, , erhälst du folgende Lösung für die gesuchte Funktion :
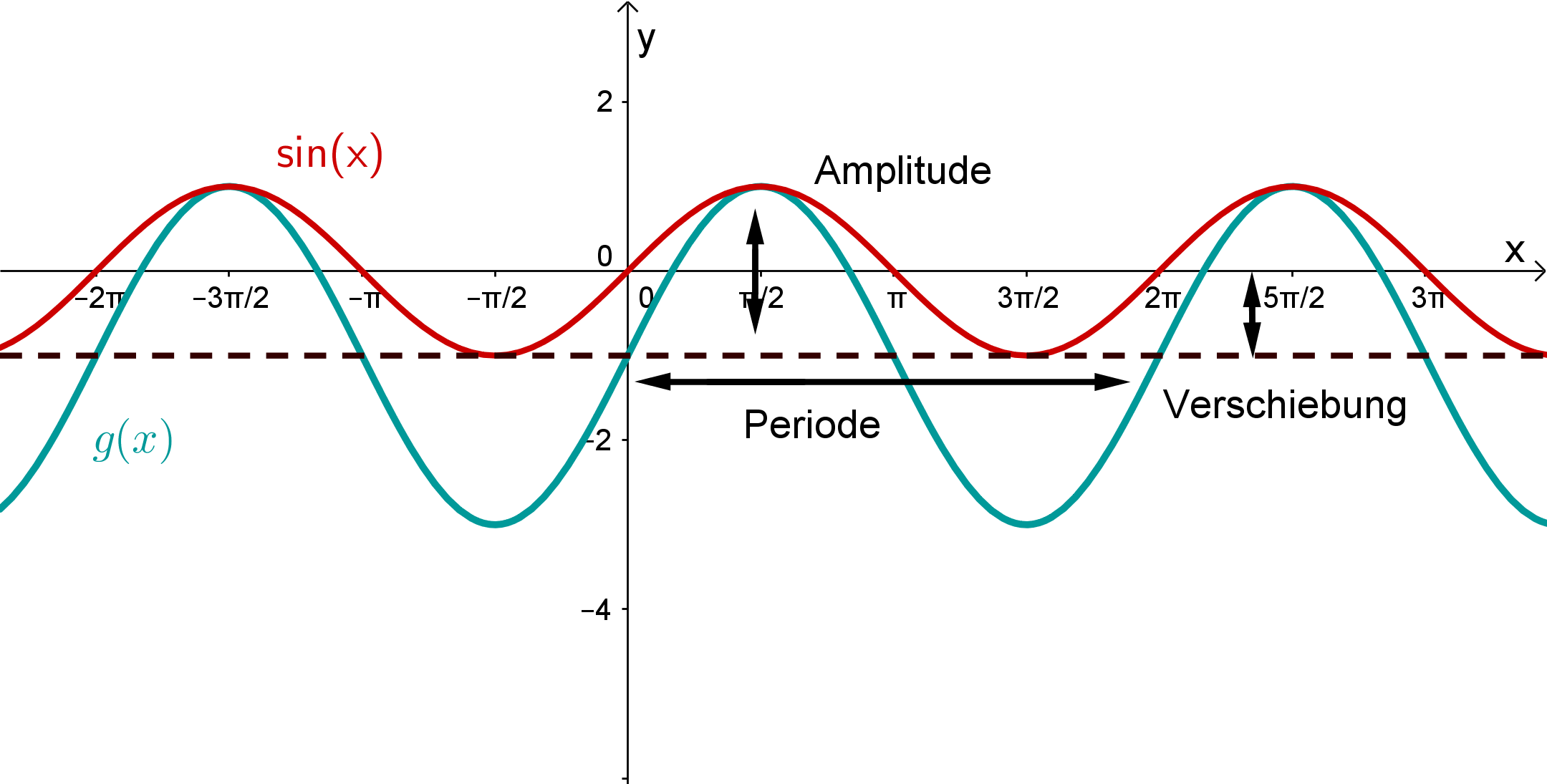
Lösung für die Funktion g(x):
Aufgrund der Punktsymmetrie bezüglich des Punktes (-1|0) muss es sich um eine Sinus-Funktion handeln.
Du kannst die Sinus-Funktion verschieben und strecken, mit der allgemeinen Funktionsgleichung: .
Betrachtest du die Amplitude der Funktion, siehst du, dass diese beträgt, das heißt für die allgemeine Funktionsgleichung, dass den Wert haben muss, weil die Amplitude der gesuchten Funktion doppelt so groß ist wie die der Funktion.
Du siehst, dass der Graph der gesuchten Funktion die selbe Periode hat wie die Funktion, das bedeutet, aus der allgemeinen Form muss den Wert haben.
Die gesuchte Funktion wurde auch nicht nach rechts oder links verschoben ,deshalb muss der Wert von aus der allgemeinen Form sein.
Betrachtest du die Verschiebung des Graphen nach unten, stellst du fest, dass die gesuchte Funktion um nach unten verschoben wurde, also hat aus der allgemeinen Form den Wert ,
Fasst du nun alle Werte der Variablen zusammen, , erhälst du folgende Lösung für die gesuchte Funktion :
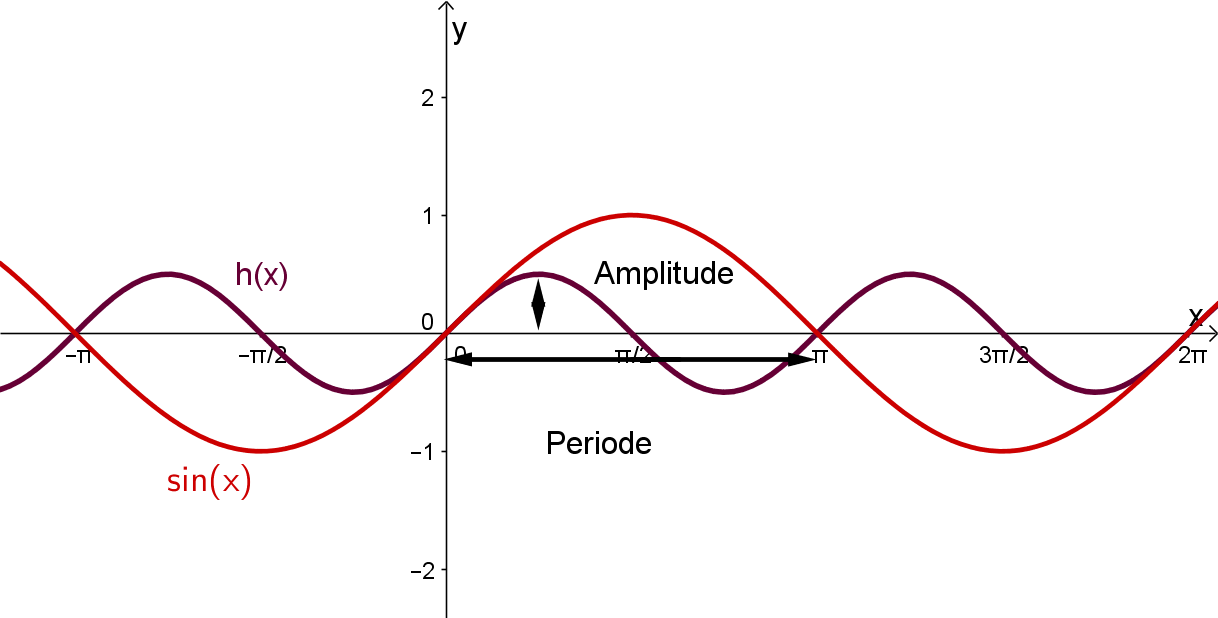
Lösung für die Funktion h(x):
Aufgrund der Punktsymmetrie bezüglich des Ursprungs muss es sich um eine Sinus-Funktion handeln.
Du kannst die Sinus-Funktion verschieben und strecken, mit der allgemeinen Funktionsgleichung: .
Betrachtest du die Amplitude der Funktion, siehst du, dass diese beträgt, das heißt für die allgemeine Funktionsgleichung, dass den Wert haben muss, weildie Amlitude der gesuchten Funktion halb so groß ist wie die der Funktion.
Betrachtest du die Periode des Graphen der gesuchten Funktion, siehst du, dass diese im Vergleich zur nur halb so groß ist(oder auch: der Sinus "läuft" doppelt so schnell). Das heißt, dass in unserer allgemeinen Form hat den Wert .
Der Graph der Funktion wurde im Vergleich zu auch nicht nach rechts oder links verschoben, das heißt der Wert von in der allgemeinen Form beträgt .
Vergleichst du den Graph mit der Funktion, siehst du, dass dieser nicht nach oben oder unten verschoben wurde, deshalb hat aus der allgemeinen Form den Wert .
Fasst du nun alle Werte der Variablen zusammen, , erhält man folgende Lösung für die gesuchte Funktion :
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
